Цепи с распределенными параметрами. Основные понятия.

Сентябрь 3, 2022

Главная
Алгебра
Цепи с распределенными параметрами. Основные понятия.

Содержание

2. В цепях с распределенными параметрами напряжения и токи будут различны на каждом участке и могут меняться
3. Элементарный участок с учетом и первичных параметров представлен на рис. Каждый участок линии длиной dx можно
4. Будем вести отсчет координаты х от начала линии и считать, что вся нагрузка сосредоточена в конце
5. Получим систему уравнений, которую называют телеграфными уравнениями однородной линии. Систему записывают с использованием частных производных, так
6. Граничные условия устанавливают связь между напряжением и током в начале или конце линии в зависимости от
7. Более краткая запись: Из системы уравнений, исключая либо ток, либо напряжение, можно получить соответственно дифференциальное уравнение
8. Аналогично можно получить решение для тока: Но такое решение нецелесообразно, так как нужно искать еще две
9. Для выяснения физического смысла слагаемых напряжения в уравнении перейдем к мгновенному значению напряжения При этом учтем,
10. Коэффициенты α и β , входящие в γ , характеризуют распространение волны вдоль линии, поэтому γ
11. Это означает, что вторая составляющая напряжения перемещается с той же скоростью, что и первая, но от
12. Коэффициентом пропорциональности между прямой и обратной волны является характеристическое (волновое) сопротивление каждой волны. В комплексной форме
14. Скачать презентацию

Слайд 2

В цепях с распределенными параметрами напряжения и токи будут
различны на каждом

участке и могут меняться в пределах одного участка.
На рис. изображен элементарный участок линии:
длина элементарного участка,
I и u – ток и напряжение в начале
участка,
ток в конце участка,
напряжение в конце участка. Такой элементарный участок обладает параметрами:
первичные параметры однородной линии, т. е. параметры линии на единицу длины. Их считают обычно известными и постоянными.

Слайд 3

Элементарный участок с учетом и первичных параметров представлен
на рис. Каждый участок

линии длиной dx
можно представить в виде Г-образного
четырехполюсника, саму линию – в
виде совокупности П- или Т-образных
четырехполюсников, включенных по-
следовательно.
Линию в целом можно рассматривать
как симметричный четырехполюсник относительно входных и выходных зажимов.
Уравнения однородной линии
Напряжение и ток линии зависят не только от времени, но и от про-
странственной координаты х (от точки линии):
Координату х можно отсчитывать от начала линии, конца или любой
точки, принятой за начало отсчета. Начало линии – точка подключения ли-
нии к генератору, конец линии – точка подключения нагрузки к линии.

Слайд 4

Будем вести отсчет координаты х от начала линии и считать, что

вся
нагрузка сосредоточена в конце линии, линия не имеет ответвлений.
Исследовать линию – это значит найти зависимости
в любой точке линии в любой момент времени.
Определим изменение напряжения на участке dx, которое равно сумме
падений напряжений на элементах этого участка:
На рис. Выше видно, что
тогда
Изменение тока в пределах этого участка равно сумме токов утечки в
элементах этого участка:
Отсюда

Слайд 5

Получим систему уравнений, которую называют телеграфными уравнениями однородной линии.
Систему записывают с

использованием частных производных, так как
напряжения и токи зависят от двух координат: t и x.
Если за начало отсчета принять конец линии и координату до рассматриваемой точки линии обозначить х′ , то получим систему уравнений (ниже), аналогичную системе (выше) но в левой части знаки изменятся на противоположные: Решение системы относительно напряжений и токов можно получить однозначно при известных начальных и граничных условиях.
Начальные условия – это значения токов и напряжений в начале или конце линии для момента времени 0 = t .

Слайд 6

Граничные условия устанавливают связь между напряжением и током
в начале или конце

линии в зависимости от режима работы линии.
Синусоидальные напряжения и токи в линии
Если линия подключена к источнику синусоидального напряжения с
частотой f, то напряжение и ток установившегося режима изменяются по си-
нусоидальному закону с той же частотой.
В системе уравнений перейдем от мгновенных значений к комплексным. Комплексные значения зависят от х и не зависят от t, так как комплекс сопоставляют вектору в момент времени
Поэтому получаем систему уравнений не в частных производных, а в
обыкновенных (полных):
Где комплексное продольное сопротивление на единицу длины линии;
комплексная поперечная проводимость на единицу длины линии.

Слайд 7

Более краткая запись:
Из системы уравнений, исключая либо ток, либо напряжение, можно

получить соответственно дифференциальное уравнение для напряжения или тока. Продифференцировав первое уравнение и подставив в него значение из второго, получим
Обозначим коэффициент распространения.
Тогда уравнение примет вид
Как известно из математики, решение этого уравнения есть сумма двух
экспоненциальных функций:
где комплекс действующего значения напряжения для любойточки линии;
постоянные интегрирования; корни характеристического уравнения,

Слайд 8

Аналогично можно получить решение для тока:
Но такое решение нецелесообразно, так как

нужно искать еще две постоянные интегрирования. Более рационально найти ток из первого уравнения системы :
Комплексное выражение зависит от первичных параметров и имеет размерность сопротивления. Его называют характеристическим или волновым сопротивлением линии и обозначают
Тогда комплекс действующего значения тока для любой точки линии
можно записать следующим образом:

Слайд 9

Для выяснения физического смысла слагаемых напряжения в уравнении перейдем к мгновенному

значению напряжения При этом учтем, что постоянные интегрирования и коэффициент распространения являются комплексными числами:
где коэффициент затухания, характеризующий степень убывания амплитуды; коэффициент фазы, характеризующий изменение фазы.
Мгновенное значение напряжения
Если считать координату х фиксированной, то первое слагаемое изменяется по синусоидальному закону с постоянной амплитудой напряжения.
Если считать фиксированным время, то напряжение меняется по синусоиде, затухающей по экспоненте.
Убывание амплитуды волны вдоль линии обусловлено потерями в линии, а изменение фазы – конечной скоростью распространения электромагнитных колебаний.

Слайд 10

Коэффициенты α и β , входящие в γ , характеризуют распространение

волны вдоль линии, поэтому γ назвали коэффициентом распространения.
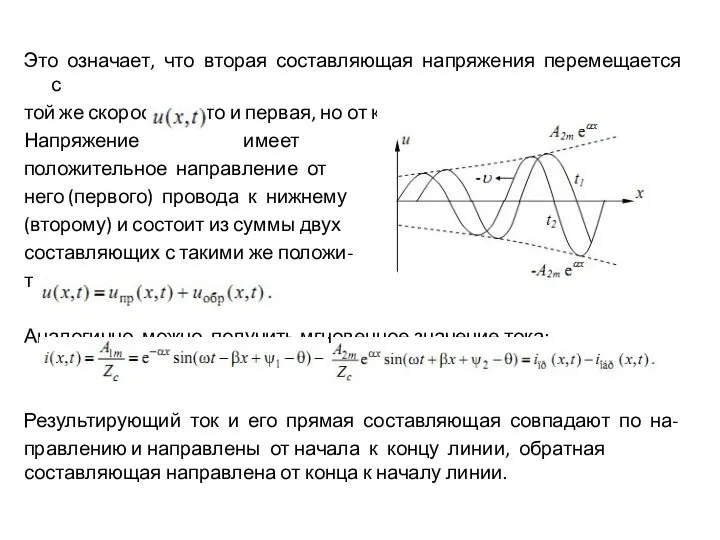
На рис. приведены волны
напряжения для двух моментов
времени
Волна перемещается от начала
линии к концу с постоянной ско-
ростью υ.
Первая составляющая напряжения имеет максимальную амплитуду
в начале линии и минимальную в конце. Эта составляющая напряжения движется от начала линии к концу со скоростью υ. Эту волну называют бегущей (прямой или падающей составляющей). Так как второе слагаемое имеет амплитуду (со знаком плюсом), то она достигает максимального значения в конце линии. Эту волну называют обратной или отраженной. В фазе колебания второе слагаемое со знаком плюс, поэтому фазовая скорость

Слайд 11

Это означает, что вторая составляющая напряжения перемещается с
той же скоростью, что

и первая, но от конца линии к началу.
Напряжение имеет
положительное направление от
него (первого) провода к нижнему
(второму) и состоит из суммы двух
составляющих с такими же положи-
тельными направлениями:
Аналогично можно получить мгновенное значение тока:
Результирующий ток и его прямая составляющая совпадают по на-
правлению и направлены от начала к концу линии, обратная составляющая направлена от конца к началу линии.

Слайд 12

Коэффициентом пропорциональности между прямой и обратной волны является характеристическое (волновое) сопротивление

каждой волны.
В комплексной форме можно записать
Напряжение и ток сдвинуты относительно друг друга по фазе на угол θ .
Мощности в цепях с распределенными параметрами для каждой волны
определяют так же, как в цепях с сосредоточенными параметрами.
Например, комплексная мощность прямой волны
Активная мощность прямой волны
Представление напряжений и токов в виде прямой и обратной составляющих есть математический прием, который облегчает анализ таких цепей.
Реально в цепях с распределенными параметрами существуют результирую-
щие напряжения и токи.

Цепи с распределенными параметрами. Основные понятия.

Содержание

В цепях с распределенными параметрами напряжения и токи будутразличны на каждом

Элементарный участок с учетом и первичных параметров представленна рис. Каждый участок

Будем вести отсчет координаты х от начала линии и считать, что

Получим систему уравнений, которую называют телеграфными уравнениями однородной линии.Систему записывают с

Граничные условия устанавливают связь между напряжением и токомв начале или конце

Более краткая запись:Из системы уравнений, исключая либо ток, либо напряжение, можно

Аналогично можно получить решение для тока:Но такое решение нецелесообразно, так как