Содержание
- 2. Определение: Преобразование логических функций с целью упрощения их аналитического представления называются минимизацией. Дизъюнктивная нормальная форма называется
- 3. Метод непосредственных преобразований логических функций Логическая функция подвергается упрощению непосредственно с помощью аксиом и теорем алгебры
- 4. Если некоторая логическая функция φ (в частном случае элементарное произведение) равна нулю на тех же наборах,
- 6. Дизъюнкция всех простых импликант называется сокращенной дизъюнктивной нормальной формой (СкДНФ) логической функции. Теорема. Любая логическая функция
- 7. Метод получения сокращенной дизъюнктивной нормальной формы логической функции называется методом Квайна. Теорема Квайна. Если в совершенной
- 8. Этапы преобразования ФАЛ по методу Квайна : Провести в СДНФ функции все возможные операции неполного склеивания
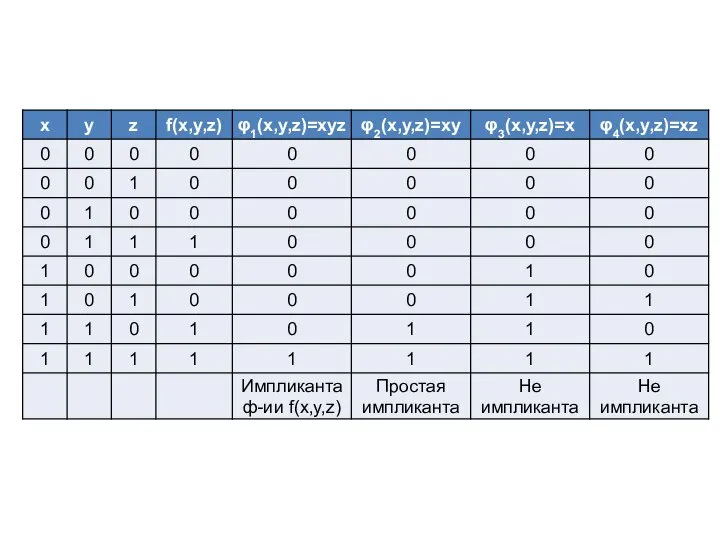
- 9. Пример. Минимизировать функцию, заданную в СДНФ: - СкДНФ
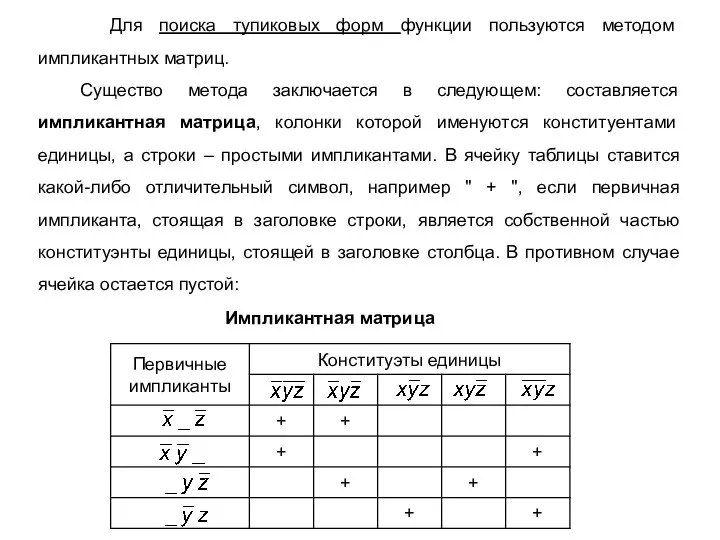
- 10. Импликантная матрица Для поиска тупиковых форм функции пользуются методом импликантных матриц. Существо метода заключается в следующем:
- 11. Вначале из всех простых импликант выбираются существенные импликанты, которые только одни покрывают какие-либо конституенты единицы данной
- 12. - существенная импликанта - существенная импликанта Тупиковые формы: Минимальные формы:
- 13. Метод Квайна-Мак-Класки. 1. Каждая конъюнкция в СДНФ представляется своим двоичным набором., где переменной, входящей в произведение
- 14. ПРИМЕР. f(a,b,c,d)СДНФ = ∑(3,7,8,10,11,12,15) Решение Этап 1. Выписать двоичное представление наборов, образующих СДНФ данной функции: (0011,
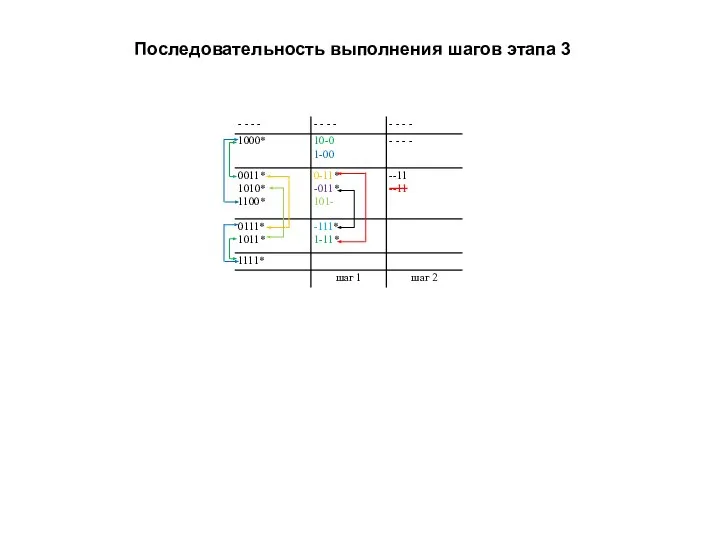
- 15. Этап 3. Сравнить каждый код из одной группы с каждым кодом из соседних групп. Если найдены
- 16. Последовательность выполнения шагов этапа 3
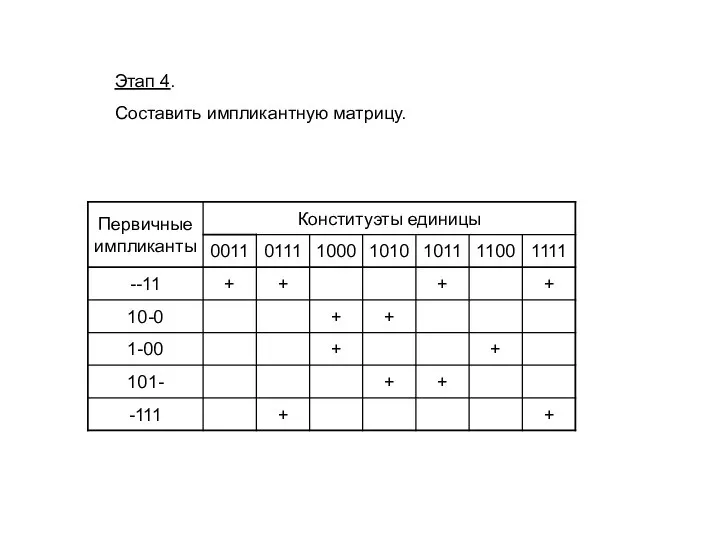
- 17. Этап 4. Составить импликантную матрицу.
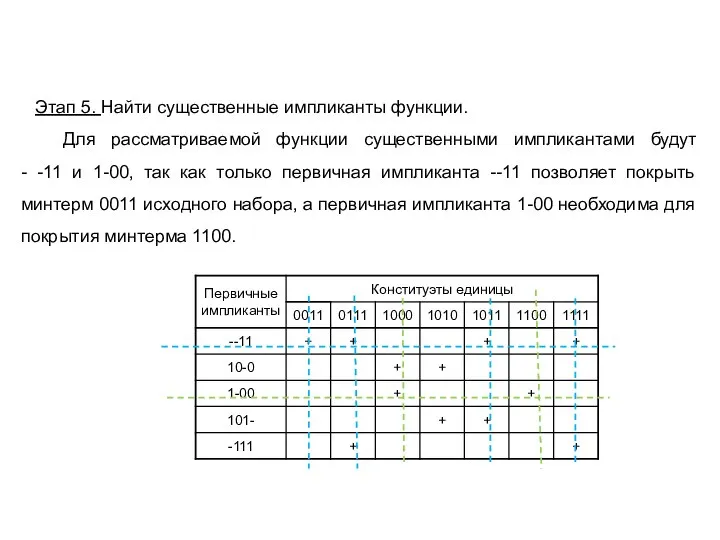
- 18. Этап 5. Найти существенные импликанты функции. Для рассматриваемой функции существенными импликантами будут - -11 и 1-00,
- 19. Этап 6. Найти тупиковые дизъюнктивные нормальные формы и выбрать из них минимальные ДНФ. Рассматриваемая функция имеет
- 20. МИНИМИЗИРУЮЩИХ КАРТ (КАРТЫ КАРНО ИЛИ ДИАГРАММЫ ВЕЙЧА) Карты Карно (их разновидностью являются диаграммы Вейча) являются графическим
- 21. Диаграмма Вейча для функции 3-х переменных Диаграмма Вейча для функции 4-х переменных
- 22. Если данную таблицу рассматривать как цилиндр, образованный соединением первой и последней колонок, то тогда склеивающиеся между
- 23. Получение минимальной ДНФ с помощью диаграмм Вейча сводится к отысканию минимального числа m-кубов максимального размера, состоящих
- 24. Пример. Минимизировать функцию, заданную в СДНФ: Минимальные формы:
- 25. Пример. Минимизировать функцию, заданную в СКНФ: f(a,b,c,d)СКНФ = ∏(2,3,5,6,7,10,11,13,14) Минимальная форма:
- 26. Неполностью определенные ФАЛ Неполностью определенной ФАЛ от n переменных называется функция, заданная на множестве наборов, меньше
- 27. ПРИМЕР. Получить методом диаграмм Вейча минимимальную дизъюнктивную нормальную форму неполностью определенной ФАЛ, заданой в следующем виде:
- 29. Скачать презентацию





















 Корейская Народно-Демократическая Республика
Корейская Народно-Демократическая Республика Празднование масленицы. Клуб «Молодые семьи г. Северодвинска»
Празднование масленицы. Клуб «Молодые семьи г. Северодвинска» Журналисты-декабристы
Журналисты-декабристы Умножение целых чисел - презентация по Алгебре
Умножение целых чисел - презентация по Алгебре Художественная культура России в первой половине XIX века
Художественная культура России в первой половине XIX века синтез спиросоединений из о-аминобензонитрила
синтез спиросоединений из о-аминобензонитрила Мониторинг закупок, аудит и контроль в сфере закупок
Мониторинг закупок, аудит и контроль в сфере закупок Исследовательская работа Тема: «Царица сибирских полей» Выволнил: Перепёлкин Матвей,
Исследовательская работа Тема: «Царица сибирских полей» Выволнил: Перепёлкин Матвей,  Религия. Тотемизм
Религия. Тотемизм Индейцы
Индейцы Моя профессия осмотрщик-ремонтник вагонов
Моя профессия осмотрщик-ремонтник вагонов Брахманизм. Религия Древней Индии
Брахманизм. Религия Древней Индии Астрология комнатных растений
Астрология комнатных растений Решение показательных неравенств Разработала учитель математики средней школы № 8 города Елабуги Герасимова Л.Н.
Решение показательных неравенств Разработала учитель математики средней школы № 8 города Елабуги Герасимова Л.Н. ТЕМА 6. Разработка и внедрение стратегии
ТЕМА 6. Разработка и внедрение стратегии  Современные войны
Современные войны Принципы создания имиджа
Принципы создания имиджа Негнойные заболевания уха
Негнойные заболевания уха Разработка сайтов для конкретных предприятий
Разработка сайтов для конкретных предприятий Налоговое право. Тема 7
Налоговое право. Тема 7 Feel'ology рroduction. Дж. Оруэлл
Feel'ology рroduction. Дж. Оруэлл Тест по СУБД
Тест по СУБД Национальная безопасность Индии
Национальная безопасность Индии Презентация В чём заключается повышение эффективности таможенного администрирования и оперативности применения мер таможенно-т
Презентация В чём заключается повышение эффективности таможенного администрирования и оперативности применения мер таможенно-т Cервисная деятельность в годы великой отечественной войны
Cервисная деятельность в годы великой отечественной войны Презентация 1 Big Data
Презентация 1 Big Data История балтийского происхождения
История балтийского происхождения Льготное кредитование для ряда отраслей сельского хозяйства Презентацию подготовил Кузнецов Павел
Льготное кредитование для ряда отраслей сельского хозяйства Презентацию подготовил Кузнецов Павел