Содержание
- 2. ГРАФ. ОПРЕДЕЛЕНИЕ Граф есть пара G = 〈V, А 〉, где V – множество вершин v,
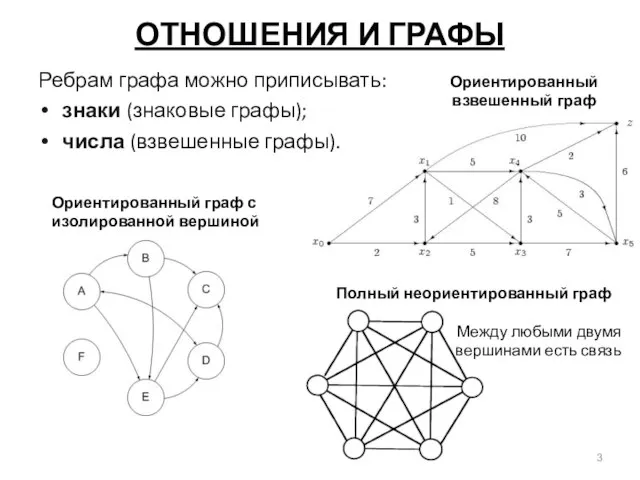
- 3. Полный неориентированный граф Между любыми двумя вершинами есть связь Ориентированный взвешенный граф ОТНОШЕНИЯ И ГРАФЫ Ребрам
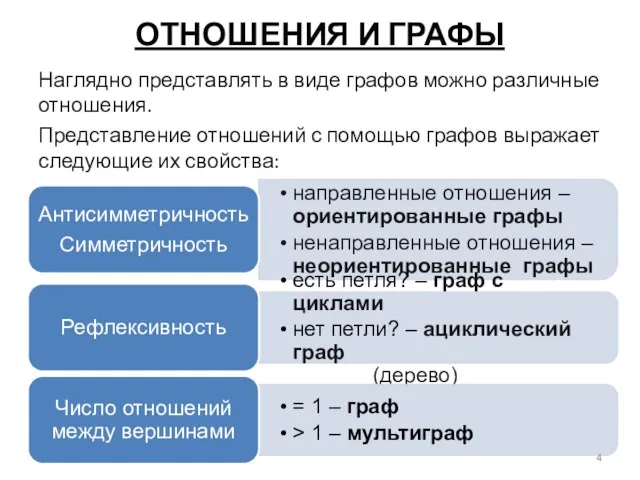
- 4. ОТНОШЕНИЯ И ГРАФЫ Наглядно представлять в виде графов можно различные отношения. Представление отношений с помощью графов
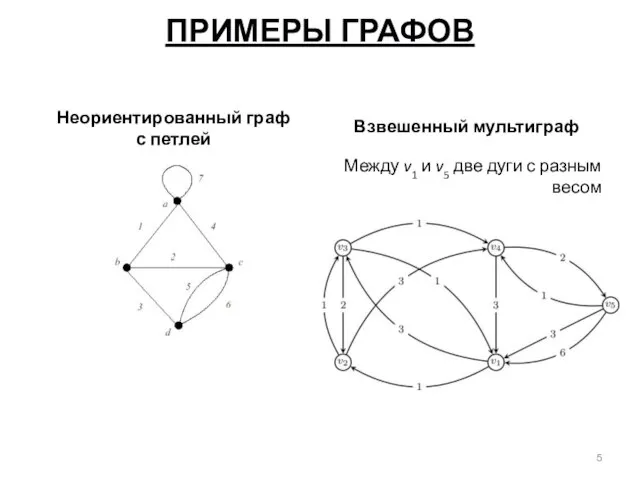
- 5. ПРИМЕРЫ ГРАФОВ Неориентированный граф с петлей Взвешенный мультиграф Между v1 и v5 две дуги с разным
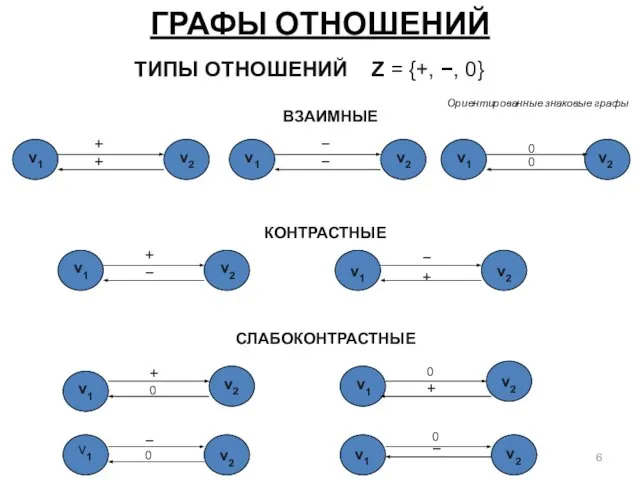
- 6. ГРАФЫ ОТНОШЕНИЙ v1 ТИПЫ ОТНОШЕНИЙ Z = {+, −, 0} ВЗАИМНЫЕ v1 v2 + + v1
- 7. ПУТЬ В ГРАФЕ Путь – термин для ориентированного графа; Цепь – для неориентированного. Путем в графе
- 8. ПУТЬ В ГРАФЕ Путь называется: простым, если все вершины vi различны; замкнутым, если vi+1 = v1;
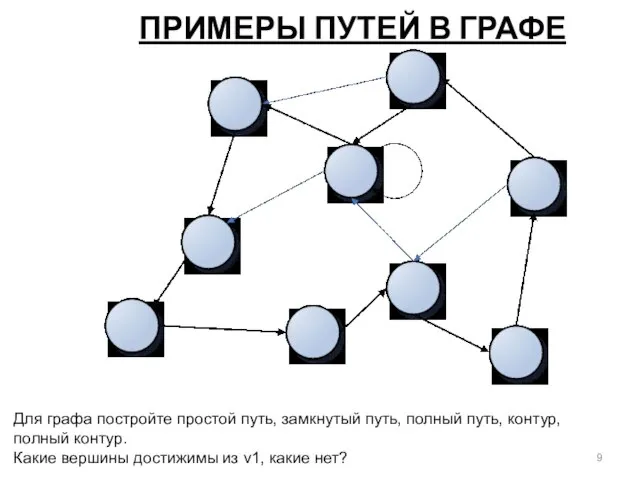
- 9. ПРИМЕРЫ ПУТЕЙ В ГРАФЕ Для графа постройте простой путь, замкнутый путь, полный путь, контур, полный контур.
- 10. ТУРНИРЫ Ориентированный граф DG = 〈 V, А 〉 называется турниром, если между любыми двумя вершинами
- 11. ХАРАКТЕРИСТИКИ ГРАФА: СВЯЗНОСТЬ Важным понятием в теории графов является понятие связности. Если для любых двух вершин
- 12. ПОКАЗАТЕЛЬ СВЯЗНОСТИ Пусть |Rmin | − минимальное число связей, необходимых для связности графа структуры. Если граф
- 13. ХАРАКТЕРИСТИКИ ГРАФА: МОЩНОСТЬ Мощностью графа называется количество дуг, связывающих две вершины. При этом дуги, имеющие встречное
- 14. ХАРАКТЕРИСТИКИ ГРАФА: РАЗМЕРНОСТЬ Размерность графа определяется общим количеством вершин и дуг, существующих в графе. В одних
- 15. ПОНЯТИЯ СМЕЖНОСТИ И ИНЦИДЕНТНОСТИ Если две различные дуги графа инцидентны одной и той же вершине, то
- 16. ПОДГРАФ, НАДГРАФ, ПОЛНЫЙ ГРАФ Подграфом ориентированного графа G называется граф, у которого все вершины и дуги
- 17. ДВУДОЛЬНЫЙ ГРАФ Двудольный граф – это граф G, множество вершин V которого можно разбить на два
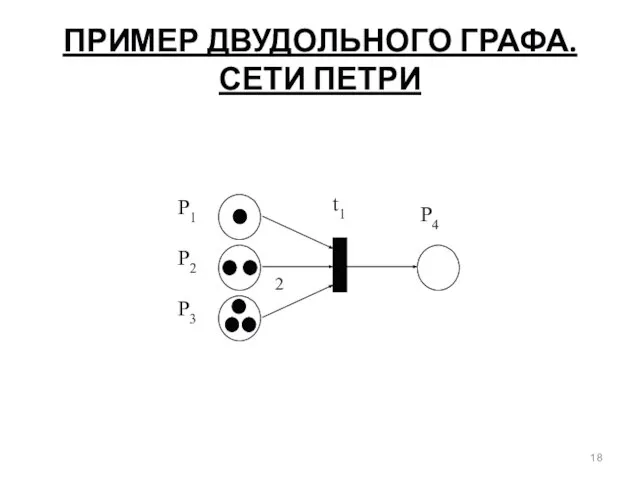
- 18. ПРИМЕР ДВУДОЛЬНОГО ГРАФА. СЕТИ ПЕТРИ
- 19. СЕТИ ПЕТРИ. ВВЕДЕНИЕ Одним из инструментов моделирования дискретных процессов, протекающих в производственных системах (ПС), являются сети
- 20. СЕТИ ПЕТРИ. ВВЕДЕНИЕ Процесс функционирования ПС отображается как изменения маркировки сети Петри, представляющей данную ПС. Маркировка
- 21. ИСПОЛЬЗОВАНИЕ СЕТЕЙ ПЕТРИ Моделирование временными сетями Петри применяют для различных целей: изучение процессов, протекающих в ПС,
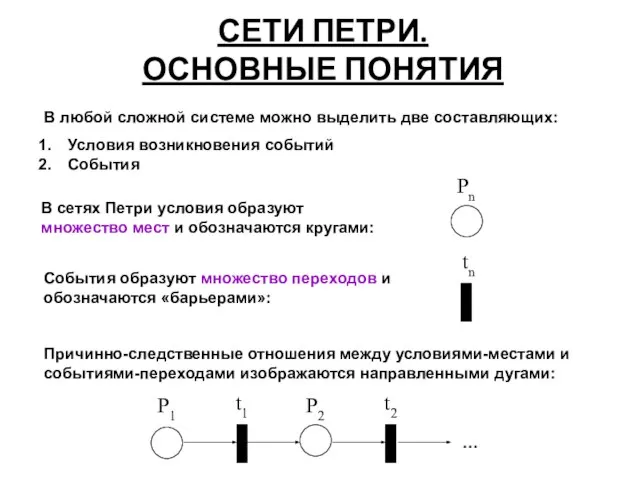
- 22. СЕТИ ПЕТРИ. ОСНОВНЫЕ ПОНЯТИЯ В любой сложной системе можно выделить две составляющих: Условия возникновения событий События
- 23. СЕТИ ПЕТРИ. РАЗМЕТКА СЕТИ Условие выполнено один раз: Pn Все условия в сети имеют кратность выполнения,
- 24. СЕТИ ПЕТРИ. ДИНАМИКА СЕТИ Динамика сети Петри представляет собой совокупность действий, которые называются срабатыванием переходов Переход
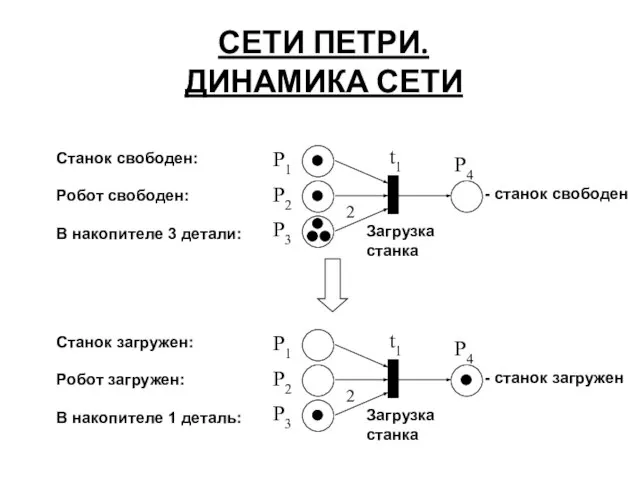
- 25. СЕТИ ПЕТРИ. ДИНАМИКА СЕТИ Станок свободен: t1 Робот свободен: В накопителе 3 детали: P1 P3 P2
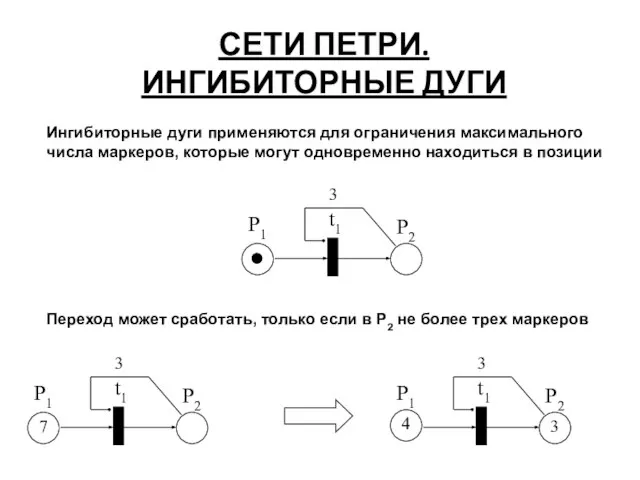
- 26. СЕТИ ПЕТРИ. ИНГИБИТОРНЫЕ ДУГИ t1 Переход может сработать, только если в P2 не более трех маркеров
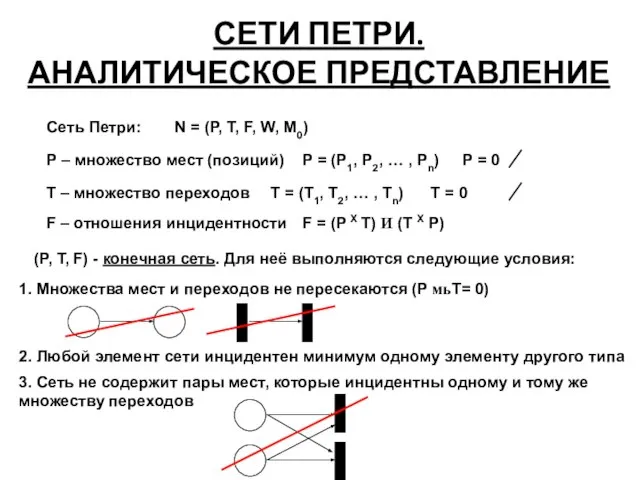
- 27. СЕТИ ПЕТРИ. АНАЛИТИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ Сеть Петри: N = (P, T, F, W, M0) 1. Множества мест
- 28. СЕТИ ПЕТРИ. АНАЛИТИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ Сеть Петри: N = (P, T, F, W, M0) W – кратности
- 29. СЕТИ ПЕТРИ. АНАЛИТИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ На основании отношений инцидентности построим матрицы дуг для данной сети: W (k,
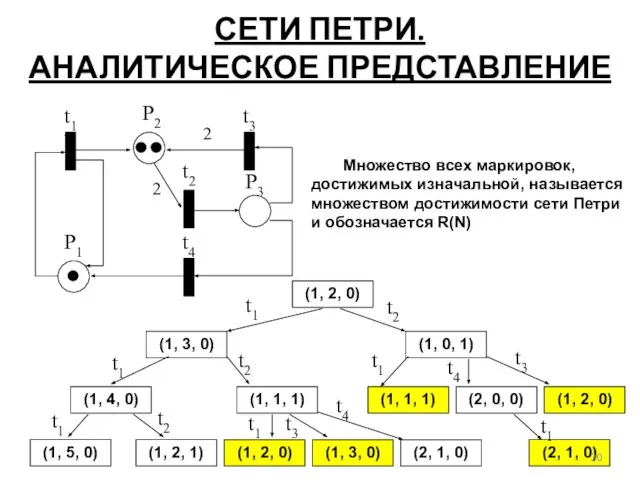
- 30. СЕТИ ПЕТРИ. АНАЛИТИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ Множество всех маркировок, достижимых изначальной, называется множеством достижимости сети Петри и обозначается
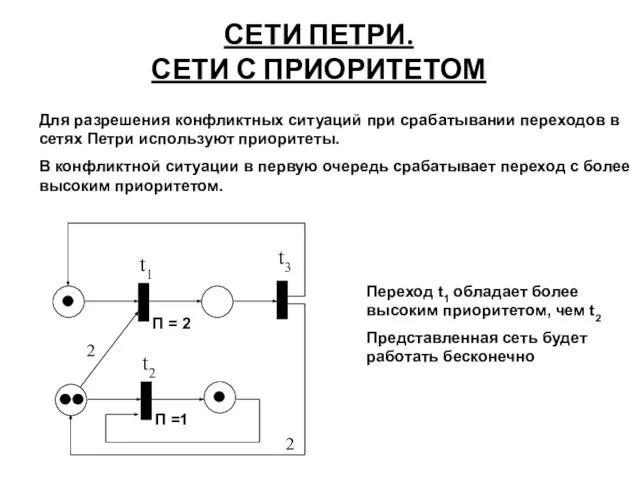
- 31. СЕТИ ПЕТРИ. СЕТИ С ПРИОРИТЕТОМ Переход t1 обладает более высоким приоритетом, чем t2 Представленная сеть будет
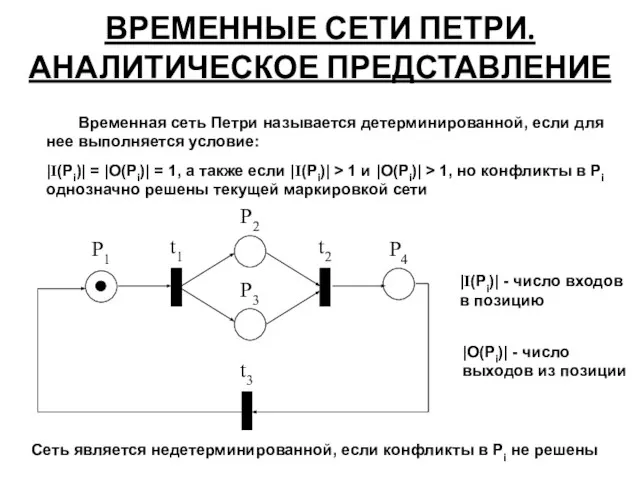
- 32. ВРЕМЕННЫЕ СЕТИ ПЕТРИ. АНАЛИТИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ Временная сеть Петри: N = (P, T, F, W, M0, Z)
- 33. ВРЕМЕННЫЕ СЕТИ ПЕТРИ. АНАЛИТИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ Временная сеть Петри называется детерминированной, если для нее выполняется условие: |I(Pi)|
- 34. СЕТИ ПЕТРИ. СВОЙСТВА СЕТИ 1. Место P сети называется ограниченным, если существует число n, такое, что
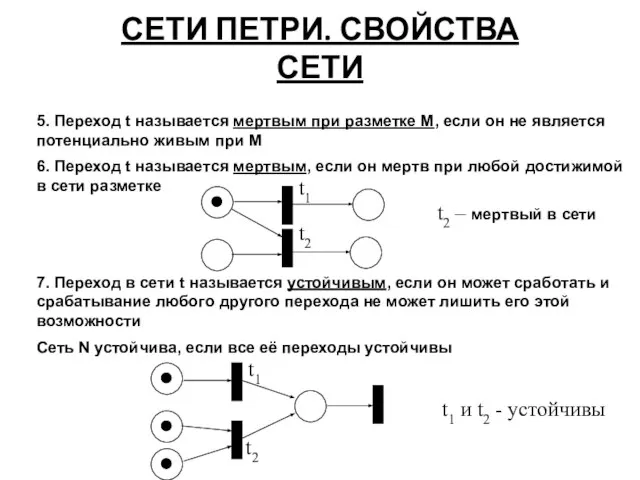
- 35. СЕТИ ПЕТРИ. СВОЙСТВА СЕТИ 5. Переход t называется мертвым при разметке M, если он не является
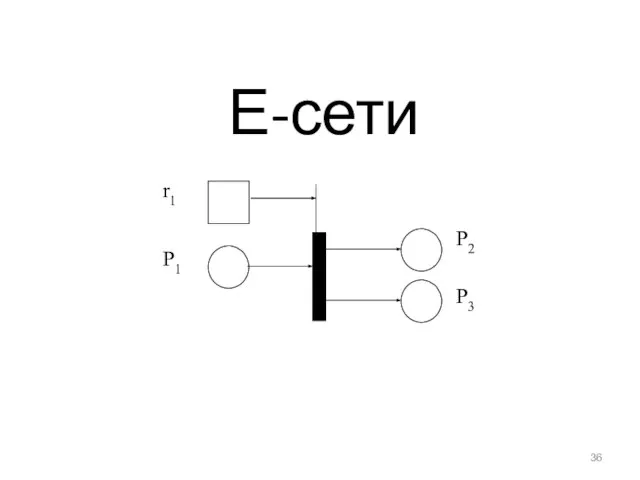
- 36. Е-сети
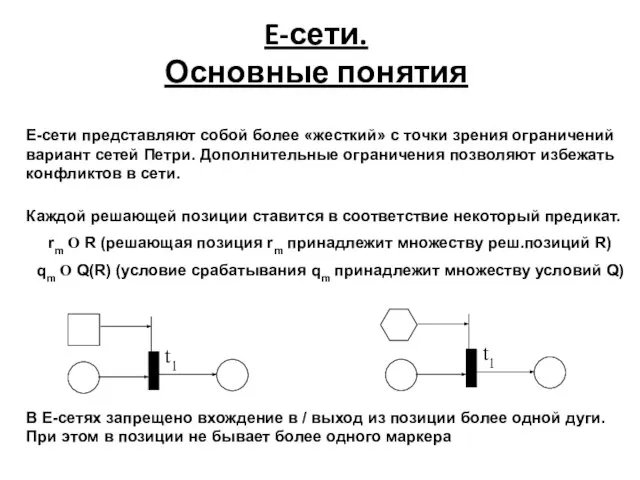
- 37. E-сети. Основные понятия Е-сети представляют собой более «жесткий» с точки зрения ограничений вариант сетей Петри. Дополнительные
- 38. E-сети. Основные понятия Прибытие в позицию маркера означает, что соответствующее условие выполнено. При попадании маркера в
- 39. E-сети. Динамика сети 1. Проверяется условие возбуждения перехода 2. Реализуется задержка времени, и в каждой выходной
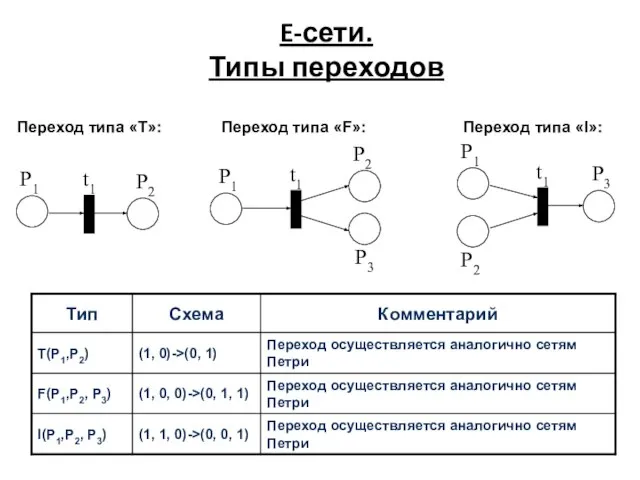
- 40. E-сети. Типы переходов Переход типа «T»: t1 P1 P2 t1 P1 P2 P3 t1 P2 P3
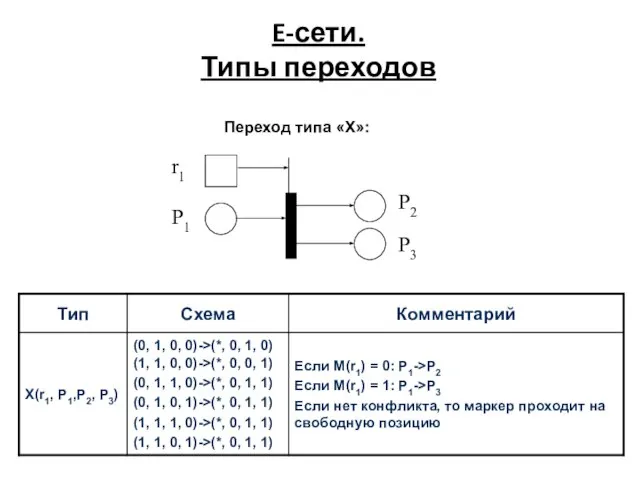
- 41. E-сети. Типы переходов r1 P2 P3 P1 Переход типа «X»:
- 42. E-сети. Типы переходов r1 P2 P3 P1 Переход типа «Y»:
- 44. Скачать презентацию























 Что такое OpenGL?
Что такое OpenGL? Презентация по информатике Компьютерные вирусы
Презентация по информатике Компьютерные вирусы  Язык программирования JAVA. Функции
Язык программирования JAVA. Функции Презентация "Архитектура компьютера" - скачать презентации по Информатике
Презентация "Архитектура компьютера" - скачать презентации по Информатике Различные типы компьютеров. Мобильные устройства
Различные типы компьютеров. Мобильные устройства Базовый курс SQL. Хранимые процедуры
Базовый курс SQL. Хранимые процедуры Работа с ПЛК cерий BX и BC
Работа с ПЛК cерий BX и BC Электронные таблицы (ЭТ) на примере MS Excel
Электронные таблицы (ЭТ) на примере MS Excel Программное обеспечение Программное обеспечение компьютера
Программное обеспечение Программное обеспечение компьютера Архитектура ЭВМ и систем: цели и задачи курса
Архитектура ЭВМ и систем: цели и задачи курса Цифровые проекты по английскому языку. Советы и рекомендации
Цифровые проекты по английскому языку. Советы и рекомендации Обработка текстовой информации
Обработка текстовой информации Геоинформационные технологии в системах территориального управления
Геоинформационные технологии в системах территориального управления Кафедра автоматизированных и вычислительных систем ВГТУ Информация для учителей и родителей (выпуск 2014 года)
Кафедра автоматизированных и вычислительных систем ВГТУ Информация для учителей и родителей (выпуск 2014 года) Аттестационная работа. Формирование ИКТ-компетентности младших школьников через применение технологий дистанционного обучения
Аттестационная работа. Формирование ИКТ-компетентности младших школьников через применение технологий дистанционного обучения Форма и элементы управления Семейство UserForm
Форма и элементы управления Семейство UserForm А.Н. Силаенков Информационные системы и технологии Лекция Основные составляющие информационных процессов и условия их реализаци
А.Н. Силаенков Информационные системы и технологии Лекция Основные составляющие информационных процессов и условия их реализаци Проект и основные этапы его разработки Информатика 10 класс по Макаровой Н.В.
Проект и основные этапы его разработки Информатика 10 класс по Макаровой Н.В. Общение в Интернете
Общение в Интернете МОБИЛЬНЫЙ ТЕЛЕФОН- ВРЕД ИЛИ ПОЛЬЗА!? Над проектом работала : ученица 11 «П» класса МОУ «Бичурга-Баишевская СО
МОБИЛЬНЫЙ ТЕЛЕФОН- ВРЕД ИЛИ ПОЛЬЗА!? Над проектом работала : ученица 11 «П» класса МОУ «Бичурга-Баишевская СО Актуальность и значимость копирайтинга в современном мире
Актуальность и значимость копирайтинга в современном мире Компьютерные вирусы. Классификации компьютерных вирусов, методы распространения, профилактики, заражения.
Компьютерные вирусы. Классификации компьютерных вирусов, методы распространения, профилактики, заражения. Анализ программ для сканирования
Анализ программ для сканирования Разработка Web-приложений на React
Разработка Web-приложений на React Ford analytics. Update
Ford analytics. Update Работа на цель. Проведение конкурсов в сети, обеспечивающих достижение конкретных целей
Работа на цель. Проведение конкурсов в сети, обеспечивающих достижение конкретных целей Переводчик будущего: нейросеть vs человек
Переводчик будущего: нейросеть vs человек Формализация понятия алгоритма
Формализация понятия алгоритма