Содержание
- 2. Лекция 5 Аналитическая геометрия 1. Аналитическое представление линии и поверхности в пространстве . 2.Плоскость в пространстве.
- 3. Аналитическое представление линии и поверхности в пространстве. Задачей аналитической геометрии является изучение геометрических объектов аналитическими методами,
- 4. В основе аналитической геометрии лежит метод координат , позволяющий описывать положение точки в пространстве с помощью
- 5. Точку М можно задать вектором Декартовыми координатами точки М называются декартовы координаты её радиус-вектора
- 6. Более сложные геометрические объекты задаются уравнениями (или неравенствами), связывающими координаты точек, образующих эти объекты.
- 7. Линия на плоскости .
- 8. Пример.
- 9. Поверхность в пространстве . Пусть - некоторая поверхность. Уравнение вида Ф(x,y,z)=0 называется уравнением этой поверхности,если ему
- 10. Пример: Поверхность - геометрическое место точек, координаты которых удовлетворяют уравнению Ф(x,y,z)=0.
- 11. Линия в пространстве . Кривую в пространстве можно рассматривать как линию пересечения двух поверхностей, то есть
- 12. Следовательно, координаты этих точек должны удовлетворять системе уравнений : (Здесь Ф1(x,y,z)=0 и Ф2(x,y,z)=0 – уравнения пересекающихся
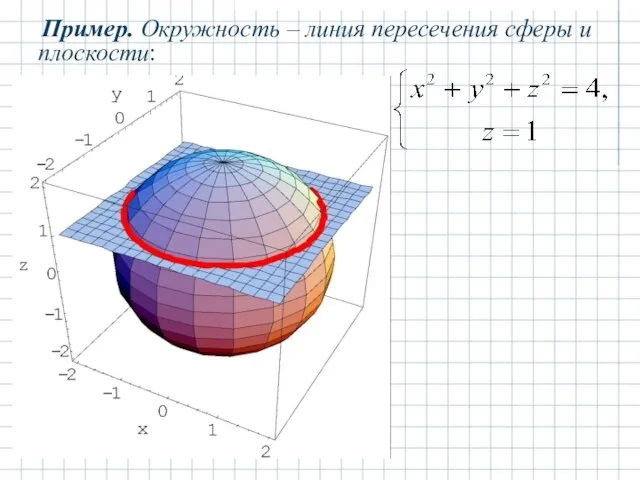
- 13. Пример. Окружность – линия пересечения сферы и плоскости:
- 14. Параметрические уравнения линии и поверхности . При параметрическом задании линии L, её можно рассматривать как траекторию
- 15. Пример: - уравнение окружности радиуса r.
- 16. Для параметрического задания поверхности S необходимы два параметра – u и v :
- 17. Пример. Уравнение сферы радиуса R:
- 18. Плоскость в пространстве. фиксированная точка плоскости. произвольная точка плоскости. - векторное уравнение плоскости. - нормальный вектор
- 19. уравнение плоскости, проходящей через точку M0(x0,y0,z0) перпендикулярно вектору . - общее уравнение плоскости.
- 20. - уравнение плоскости «в отрезках». Здесь P1(a,0,0), P2(0,b,0), P3(0,0,c) – точки пересечения плоскости с координатными осями,
- 21. Пример.
- 22. Угол между двумя плоскостями . Рассмотрим
- 23. Условие перпендикулярности двух плоскостей. Условие параллельности двух плоскостей.
- 24. Прямая в пространстве. - произвольная точка прямой
- 25. - векторное уравнение прямой. - канонические уравнения прямой. - параметрические уравнения прямой.
- 26. - общие уравнения прямой. Эти уравнения определяют прямую как линию пересечения двух не параллельных плоскостей .
- 27. Угол между двумя прямыми Если
- 28. Угол между прямой и плоскостью. Пусть
- 29. Условие параллельности двух прямых. Условие перпендикулярности двух прямых.
- 30. Условие параллельности прямой и плоскости. Условие перпендикулярности прямой и плоскости.
- 31. Условие скрещиваемости двух прямых. Две прямые называются скрещивающимися, если они не лежат в одной плоскости. Если
- 32. МКТ 7 1. Записать координаты нормального вектора плоскости 2. Какое произведение векторов использовано в условии ортогональности
- 34. Скачать презентацию






























 Математическое моделирование
Математическое моделирование Визначення площі многокутника
Визначення площі многокутника Длина окружности. Решение задач
Длина окружности. Решение задач Теория вероятностей и математическая статистика
Теория вероятностей и математическая статистика Векторы на плоскости и в пространстве
Векторы на плоскости и в пространстве Площадь криволинейной трапеции
Площадь криволинейной трапеции Статистические характеристики: среднее арифметическое, мода, медиана называются средними результатами измерений
Статистические характеристики: среднее арифметическое, мода, медиана называются средними результатами измерений Презентация по математике "Простые и составные числа" - скачать бесплатно
Презентация по математике "Простые и составные числа" - скачать бесплатно Игра – зачет по теме
Игра – зачет по теме Тест «Многогранники, вписанные в сферу»
Тест «Многогранники, вписанные в сферу» Простые геометрические фигуры
Простые геометрические фигуры Геометричні перетворення графіків функцій
Геометричні перетворення графіків функцій Алгебра и начало анализа. Функция y=cos x
Алгебра и начало анализа. Функция y=cos x Первообразная. Неопределенный интеграл
Первообразная. Неопределенный интеграл Пифагор и его теорема
Пифагор и его теорема Презентация по математике "ТРЕНАЖЕРЫ ПО МАТЕМАТИКЕ ДЛЯ ПОДГОТОВКИ К ЕГЭ 2015" - скачать бесплатно
Презентация по математике "ТРЕНАЖЕРЫ ПО МАТЕМАТИКЕ ДЛЯ ПОДГОТОВКИ К ЕГЭ 2015" - скачать бесплатно Измерение углов транспортиром
Измерение углов транспортиром Ребусы. Математика
Ребусы. Математика Выпуклый анализ. Субградиент и субдифференциал функции. Лекция 20
Выпуклый анализ. Субградиент и субдифференциал функции. Лекция 20 Решение задач. (6 класс)
Решение задач. (6 класс) Прямая пропорциональность 7 класс 2012 год
Прямая пропорциональность 7 класс 2012 год  Круговые диаграммы
Круговые диаграммы Численные методы решения нелинейных и трансцендентных уравнений
Численные методы решения нелинейных и трансцендентных уравнений Подготовка к ЕГЭ. Задания с развернутым ответом повышенного уровня сложности С5
Подготовка к ЕГЭ. Задания с развернутым ответом повышенного уровня сложности С5 Развитие логического мышления младших школьников на уроках математики
Развитие логического мышления младших школьников на уроках математики Классическая вероятность
Классическая вероятность Презентация Финансовые ренты (продолжение)
Презентация Финансовые ренты (продолжение) Способ сложения при решении систем линейных уравнений
Способ сложения при решении систем линейных уравнений