Содержание
- 2. Определение: Дифференциальное исчисление Дифференцируемость функции где А – некоторое число; о(Δx) – бесконечно малая функция более
- 3. Теорема: Дифференциальное исчисление Дифференцируемость функции Если функция f (x) дифференцируема в точке x0 , то она
- 4. Дифференциальное исчисление Дифференциал функции Из определения дифференцируемости функции и её производной получаем, что Если то Значит,
- 5. Определение: Дифференциальное исчисление Дифференциал функции Таким образом, по определению Главная линейная часть приращения функции f (x)
- 6. Дифференциальное исчисление Дифференциал функции Рассмотрим функцию у = х. То есть, приращение и дифференциал независимой переменной
- 7. Дифференциальное исчисление Перепишем выражение для дифференциала функции в виде Пусть y = f (x) – некоторая
- 8. Дифференциальное исчисление Свойства дифференциала функции Для дифференциалов двух функций f (x) и g(x) справедливы следующие формулы:
- 9. Пример: Решение: в точке х0 = 1. Найти дифференциал функции Дифференциальное исчисление Дифференциал функции Автор: И.В.
- 10. Дифференциальное исчисление Приложения дифференциала функции С помощью дифференциала можно приближённо вычислять значения функции f (x) для
- 11. Пример: Решение: Вычислить приближённо Дифференциальное исчисление Приложения дифференциала функции Автор: И.В. Дайняк, к.т.н., доцент Кафедра высшей
- 12. Пусть f (x) – сложная дифференцируемая функция, где x = ϕ (t) – дифференцируемая функция. Дифференциальное
- 13. Дифференциал функции всегда равен произведению её производной на дифференциал аргумента и не зависит от того, является
- 15. Скачать презентацию












 Математик на фабрике обоев или алгоритмическое рисование узоров
Математик на фабрике обоев или алгоритмическое рисование узоров Древнегреческий физик, математик и инженер Архимед
Древнегреческий физик, математик и инженер Архимед Применение дифференциала в приближенных вычислениях
Применение дифференциала в приближенных вычислениях ОГЭ 2016. Модуль Геометрия №12
ОГЭ 2016. Модуль Геометрия №12 Множества и операции над ними (9 класс)
Множества и операции над ними (9 класс)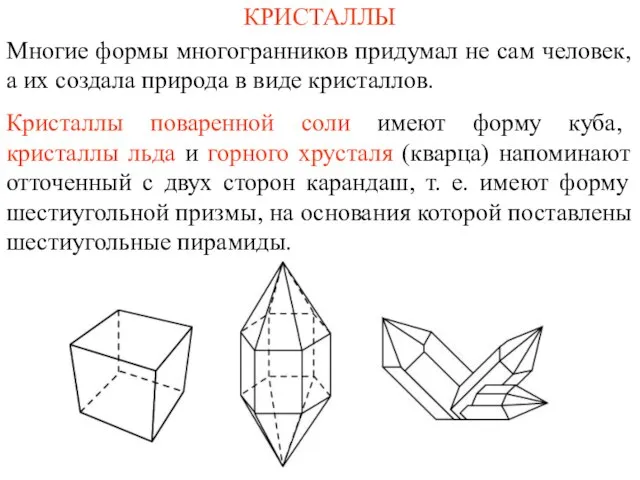 Кристалы - природные многогранники
Кристалы - природные многогранники Алгоритмическая разрешимость. Алгоритмически неразрешимые задачи
Алгоритмическая разрешимость. Алгоритмически неразрешимые задачи Подобные треугольники
Подобные треугольники Линейные неравенства с одним неизвестным
Линейные неравенства с одним неизвестным Параллельный перенос и поворот
Параллельный перенос и поворот Приближенные значения чисел. Округление чисел
Приближенные значения чисел. Округление чисел Разложение числа на простые множители
Разложение числа на простые множители Математика. Часть 2
Математика. Часть 2 Требования к математической подготовке учащихся к началу основной школы
Требования к математической подготовке учащихся к началу основной школы Взаимная перпендикулярность фигур. Задание многогранников на эпюре Монжа. (Лекция 7)
Взаимная перпендикулярность фигур. Задание многогранников на эпюре Монжа. (Лекция 7) Сложение и вычитание десятичных дробей
Сложение и вычитание десятичных дробей Урок в 5 классе Составила учитель математики и информатики, II дидактическая степень, Арнаут Алла Л. АТО, Гагаузия, Комратский райо
Урок в 5 классе Составила учитель математики и информатики, II дидактическая степень, Арнаут Алла Л. АТО, Гагаузия, Комратский райо Степенная функция, её свойства и график
Степенная функция, её свойства и график Наближене обчислення визначеного інтегралу від функції однієї змінної
Наближене обчислення визначеного інтегралу від функції однієї змінної Корреляционный анализ
Корреляционный анализ Формирование познавательного интереса школьников к учению на уроках математики
Формирование познавательного интереса школьников к учению на уроках математики Презентация по математике "Квадратичная функция и её график" - скачать бесплатно
Презентация по математике "Квадратичная функция и её график" - скачать бесплатно Аттестационная работа. Курс дополнительного образования «Математическая эстафета»
Аттестационная работа. Курс дополнительного образования «Математическая эстафета» Решение логарифмических уравнений
Решение логарифмических уравнений Системы рациональных неравенств. 9 класс
Системы рациональных неравенств. 9 класс Сфера и шар. 12 класс
Сфера и шар. 12 класс Алгоритм сложения трехзначных чисел с двумя переходами через разряд
Алгоритм сложения трехзначных чисел с двумя переходами через разряд Область определения и область значения функций
Область определения и область значения функций