Содержание
- 2. ДИСКРЕТНІ ВИПАДКОВІ ВЕЛИЧИНИ Математичне очікування дискретної випадкової величини Визначення: Математичним очікуванням М(Х) випадкової величини X називається
- 3. Властивості математичного очікування дискретної випадкової величини М(С) = С⋅1 = С М(СХ) = СМ(X) М(Х+У) =
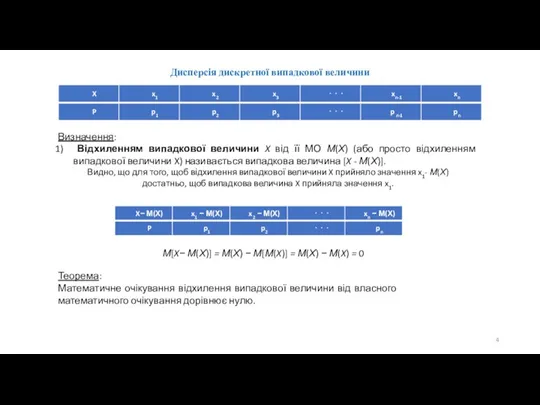
- 4. Дисперсія дискретної випадкової величини Визначення: Відхиленням випадкової величини X від її МО М(Х) (або просто відхиленням
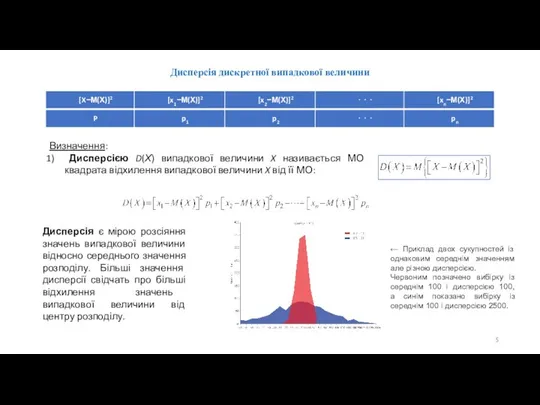
- 5. Дисперсія дискретної випадкової величини Визначення: Дисперсією D(Х) випадкової величини X називається МО квадрата відхилення випадкової величини
- 6. Властивості дисперсії дискретної випадкової величини
- 7. Середнє квадратичне відхилення Середнє квадратичне відхилення — у теорії ймовірностей один із найпоширеніших показників розсіювання (розкиду)
- 8. ЗАДАЧА ПРО ПОВТОРЕННЯ ВИПРОБУВАНЬ (ДОСЛІДІВ) Біноміальний розподіл Постановка задачі: Нехай проводиться n випробувань, причому ймовірність появи
- 9. Біноміальний розподіл Знову розглянемо n незалежних випробувань, в кожному з яких настає подія А з ймовірністю
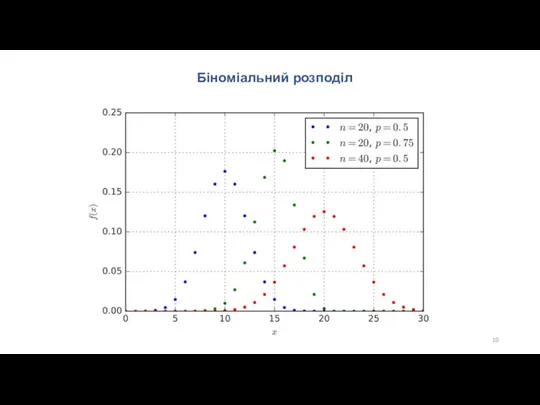
- 10. Біноміальний розподіл
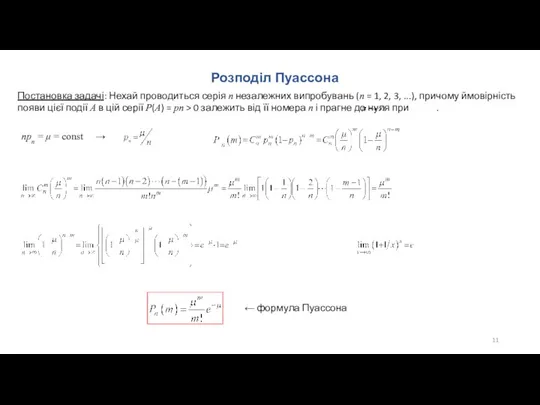
- 11. Розподіл Пуассона Постановка задачі: Нехай проводиться серія n незалежних випробувань (n = 1, 2, 3, ...),
- 12. Розподіл Пуассона Визначення: Кажуть, що випадкова величина Х визначена за законом Пуассона, якщо ця величина задана
- 14. Скачать презентацию







 Деление дробей (6 класс) - Презентация по математике_
Деление дробей (6 класс) - Презентация по математике_ Алгебра. Подготовка к ЕГЭ
Алгебра. Подготовка к ЕГЭ Арифметическая прогрессия
Арифметическая прогрессия Задание на треугольники
Задание на треугольники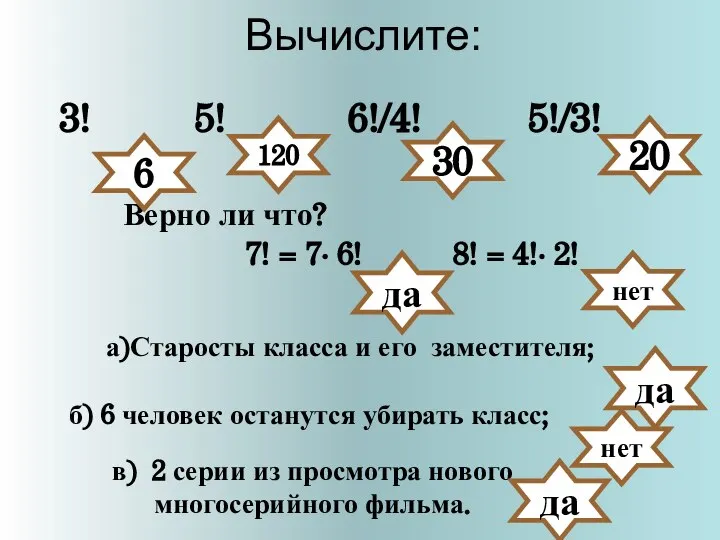 Вычислите:
Вычислите:  Многочлены от одной переменной
Многочлены от одной переменной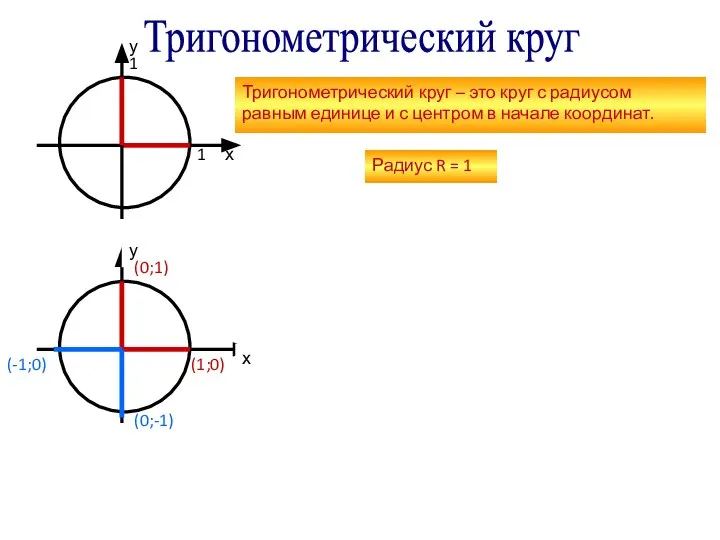 Тригонометрический круг
Тригонометрический круг Подготовка к ЕГЭ по математике. Решение уравнений и неравенств задание В4
Подготовка к ЕГЭ по математике. Решение уравнений и неравенств задание В4 Интеллектуальная игра «Ох, уж эта математика!»
Интеллектуальная игра «Ох, уж эта математика!» Блочная система обучения математике
Блочная система обучения математике Интегрированная система Maple
Интегрированная система Maple Теорема Пифагора Различные формулировки
Теорема Пифагора Различные формулировки  Презентация по математике "Вкусные числа" - скачать
Презентация по математике "Вкусные числа" - скачать  Роль Франсуа Виета в математике
Роль Франсуа Виета в математике Пирамида в задачах ЕГЭ
Пирамида в задачах ЕГЭ УРОК МАТЕМАТИКИ УМК «ШКОЛА РОССИИ» Автор Молчанова М.А., учитель начальных классов МОУ СОШ № 21 с. Пушкинское Гулькеви
УРОК МАТЕМАТИКИ УМК «ШКОЛА РОССИИ» Автор Молчанова М.А., учитель начальных классов МОУ СОШ № 21 с. Пушкинское Гулькеви Математика 5 класс МБОУ СОШ №7 г.Лобня учитель математики Фокина Надежда Николаеевна
Математика 5 класс МБОУ СОШ №7 г.Лобня учитель математики Фокина Надежда Николаеевна  Комплeксные числа. Арифметические операции над ними (10 класс)
Комплeксные числа. Арифметические операции над ними (10 класс) Математический анализ
Математический анализ Презентация на тему Сложение и вычитание
Презентация на тему Сложение и вычитание Типы текстовых задач в ЕГЭ
Типы текстовых задач в ЕГЭ Сложение и вычитание положительных и отрицательных чисел
Сложение и вычитание положительных и отрицательных чисел Умножение десятичных дробей Урок математики в 5 классе по теме:
Умножение десятичных дробей Урок математики в 5 классе по теме:  Работа учителя математики на уроке по подготовке к олимпиадам
Работа учителя математики на уроке по подготовке к олимпиадам Простейшие задачи в координатах
Простейшие задачи в координатах Моменты случайной величины
Моменты случайной величины Преобразование графиков функций
Преобразование графиков функций Смежные и вертикальные углы
Смежные и вертикальные углы