Содержание
- 2. Цель работы - выяснить, что является функциональным уравнением и их системами, найти способы решения и составить
- 3. ЗАДАЧИ ИССЛЕДОВАНИЯ: ИЗУЧЕНИЕ И АНАЛИЗ ЛИТЕРАТУРЫ; ПОИСК СПОСОБОВ РЕШЕНИЯ ФУНКЦИОНАЛЬНЫХ УРАВНЕНИЙ И ИХ СИСТЕМ; РЕШЕНИЕ ФУНКЦИОНАЛЬНЫХ
- 4. Определение: Функциональным уравнением называют уравнение, в котором неизвестным является функция, связанная при помощи образования сложной функции
- 5. Определение: Решением функционального уравнения называется всякая функция, при подстановке которой в функциональное уравнение вместо неизвестной функций
- 6. Некоторые функциональные уравнения знакомы нам еще из школьного курса это Они задают такие свойства функций, как
- 7. Определение. Если в числовом множестве Х вместе с любым его элементом х содержится и элемент- х,
- 8. Определение. Если область определения функции y=f(x) является симметричным множеством и для любого аргумента х выполняется равенство
- 9. Пример Определим четность или нечетность функций:
- 10. - четная - нечетная -ни четная ни нечетная Решение - четная - четная
- 11. Определение. Если найдется такое чисто Т≠0, что для любых х из области определения функции y=f(x) выполняется
- 12. Из курса алгебры для 9 класса известно, что для функций y=sinx, y=cosx соответственно выполняется равенства sin(x+2π)=sinx,
- 13. Пусть функция у = f(х) возрастает на R. Решите уравнение: f(3х + 2) = f(4х2 +
- 14. Примеры решения функциональных уравнений методом подстановки. Пример. Найти f(x) Решение 1) Пусть тогда 2) Подставим в
- 15. 4)Итак, получили два уравнения: 5)Умножим обе части 1-го уравнения на (-2) и сложим со 2-ым уравнением,
- 16. 1) Пусть, 2) Подставим в исходное уравнение, получим 3) Заменим z на получим или после преобразований
- 17. 4)Итак, получили два уравнения: 5)Умножим обе части 1-го уравнения на (-2) и сложим со 2-ым уравнением,
- 18. Тогда ответ:
- 19. Пример: 1) Заменим в уравнении x на 1-x, получим 2) Умножим обе части исходного уравнения на
- 20. Пример f(x)+xf(1-x)=1+x Заменим x на 1-x, получим f(1-x)+(1-x)f(x)=1+1-x Умножим обе части уравнения f(1-x)+(1-x)f(x)=2-x на x и
- 21. Пример 2f(3-x)+3f(x-1)=2x-1 1)Пусть x=3-t, тогда уравнение принимает вид: 2∙f(3-3+t)+3f(3-t-1)=2(3-t)-1 2∙f(t)+3f(2-t)=5-2t 2)Пусть x=t+1, тогда исходное уравнение принимает
- 22. Пример Заменим x на получим или 2)Умножим обе части уравнения из п.1 на (-2) и сложим
- 23. …
- 24. Классические функциональные уравнения В математике есть несколько типов относительно простых функциональных уравнений, решения которых хорошо известны
- 25. Найти x, если Решение Рассмотрим уравнение: Получим: Если функция нечетная то -f(3x)=f(-3x) Проверим: -нечетная Значит f(2x+1)=f(-3x)
- 26. Решить неравенство: если функция f(x) и g(x) удовлетворяют системе Решение Умножим второе уравнение на -1 и
- 27. 2)Вернемся к системе: Умножим первое уравнение на 2 и сложим со вторым: Получим: Введем замену Получим:
- 28. Решим неравенство: Ответ:
- 30. Скачать презентацию



























 Развитие математики в России «Стоит только показать, что какая-либо вещь невозможна, как найдется математик, который ее сделает.»
Развитие математики в России «Стоит только показать, что какая-либо вещь невозможна, как найдется математик, который ее сделает.» Развёртка параллелепипеда, куба, треугольной и четырёхугольной пирамиды. 5 класс
Развёртка параллелепипеда, куба, треугольной и четырёхугольной пирамиды. 5 класс Построение графика квадратичной функции
Построение графика квадратичной функции Увлекательная математика
Увлекательная математика Презентация на тему Компьютер
Презентация на тему Компьютер Элементы теории вероятностей
Элементы теории вероятностей Логарифмы. Решение логарифмических уравнений и неравенств
Логарифмы. Решение логарифмических уравнений и неравенств Основные понятия планиметрии
Основные понятия планиметрии Степень с натуральным показателем. Урок - Лаборатория
Степень с натуральным показателем. Урок - Лаборатория Смежные и вертикальные углы. Равенство геометрических фигур
Смежные и вертикальные углы. Равенство геометрических фигур Презентация по математике "Королевство Математики" - скачать
Презентация по математике "Королевство Математики" - скачать  Площади фигур
Площади фигур Иностранные меры длины
Иностранные меры длины Отбор корней при решении тригонометрических уравнений
Отбор корней при решении тригонометрических уравнений Задание В 3 ЕГЭ. Планиметрия: вычисление длин и площадей
Задание В 3 ЕГЭ. Планиметрия: вычисление длин и площадей Уравнение прямой на плоскости
Уравнение прямой на плоскости  Уравнения с разделяющимися переменными. Однородные уравнения. (Семинар 33)
Уравнения с разделяющимися переменными. Однородные уравнения. (Семинар 33) Нули функции
Нули функции Презентация на тему Умножение чисел, оканчивающихся нулями
Презентация на тему Умножение чисел, оканчивающихся нулями Основные задачи на дроби
Основные задачи на дроби Интеграл. Математика - гимнастика ума
Интеграл. Математика - гимнастика ума Математический КВН
Математический КВН Свойства показательной функции
Свойства показательной функции Многогранники. Урок-лекция
Многогранники. Урок-лекция Чи такі вони прості ці прості числа?
Чи такі вони прості ці прості числа? Готовимся к итоговой аттестации
Готовимся к итоговой аттестации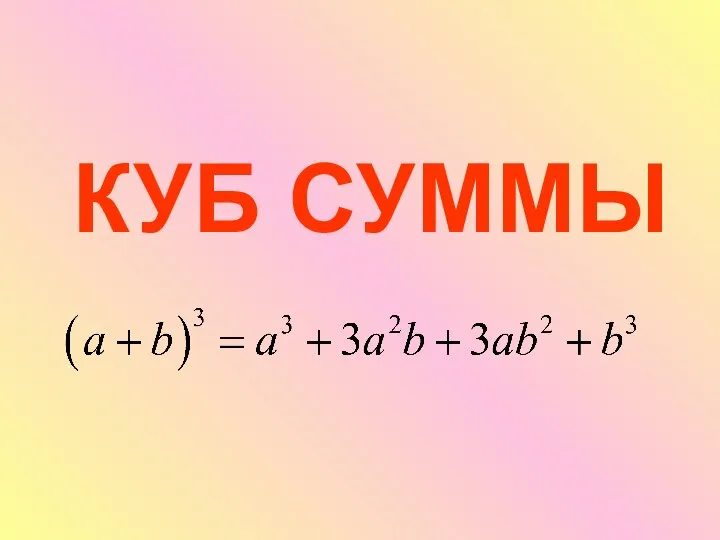 Куб суммы
Куб суммы Параллельные прямые. Геометрия 7 класс
Параллельные прямые. Геометрия 7 класс