Содержание
- 2. Составляющая N z, называемая продольной (нормальной) силой, вызывает деформацию растяжения или сжатия.
- 3. При деформации растяжения сжатия площадь поперечного сечений полностью характеризовала прочность и жесткость детали.
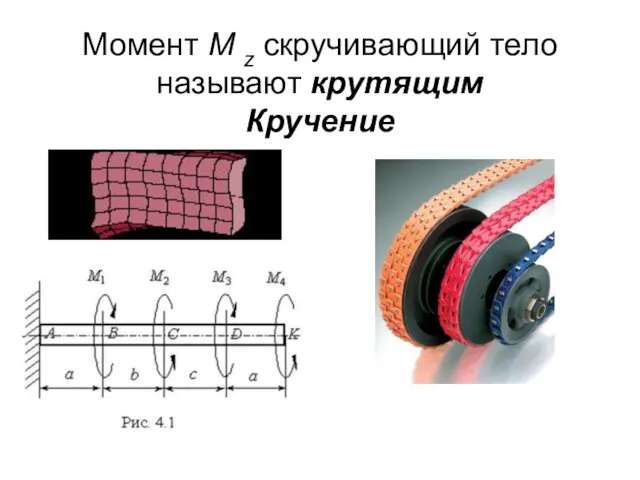
- 4. Момент M z скручивающий тело называют крутящим Кручение
- 5. Моменты M x и M y изгибают тело и называются изгибающими. Изгиб.
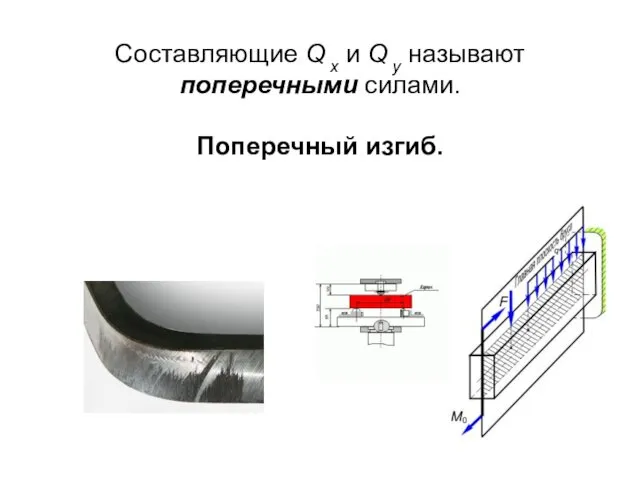
- 6. Составляющие Q x и Q y называют поперечными силами. Поперечный изгиб.
- 7. Однако при деформации изгиба и кручения прочность и жесткость характеризуются не только размерами сечения, но и
- 8. Статические моменты площадей Координаты zc и ус центра тяжести плоской фигуры определяются, как известно из общей
- 10. Статический момент площади фигуры относительно какой-либо оси равен сумме статических моментов частей, из которых состоит фигура,
- 11. Различают осевые, полярные и центробежные моменты инерции. Осевым моментом инерции сечения называют взятую по всей площади
- 13. Полярным моментом инерции (моментом инерции относительно полюса) называют взятую по всей площади сечения сумму произведений элементарных
- 14. Центробежным моментом инерции сечения называют взятую по всей площади сечения сумму произведений элементарных пло-щадок на обе
- 15. Из приведенных определений следует, что момент инерции сложной фигуры равен сумме моментов инерции ее частей. Полярный
- 16. Момент инерции сечения относительно какой-либо оси равен моменту инерции этого сечения относительно центральной оси, параллельной данной,
- 17. Центробежным моментом инерции сечения называют взятую по всей площади сечения сумму произведений элементарных площадок на обе
- 19. Две взаимно перпендикулярные оси с началом в данной точке, для которых центробежный момент инерции плоской фигуры
- 20. главные центральные оси инерции фигуры могут быть найдены, если известны ее центробежный J zy и осевые
- 21. Моменты инерции относительно главных центральных осей инерции называют главными моментами инерции: они обладают тем свойством, что
- 22. Определим величины моментов инерции наиболее распространенных плоских сечений, встречающихся при расчетах и конструировании деталей механизмов.
- 23. Прямоугольник высотой h и шириной b. Выделим в прямоугольнике элементарную полоску высотой dy и шириной b.
- 24. Круговое кольцо с наружным диаметром D и внутренним d. В данном случае полярный момент инерции может
- 25. Обозначив d/D=C, после подстановки в выражение‘ получим из соотношения находим осевые моменты инерции круга и кругового
- 26. Для круга с учетом соотношения
- 27. Для кольца
- 29. Дано h1 = 45 мм b1 = 66 мм h2 = 36 мм b2= 140 мм
- 30. Статические моменты инерции относительно выбранных осей Ось X S 1x= А 1 * y1 =2970*40.5=120285 мм3
- 31. Ось Y S 1y= А 1 * x1 =2970*(-9)=26730 мм3 S 2y= А 2 * x2
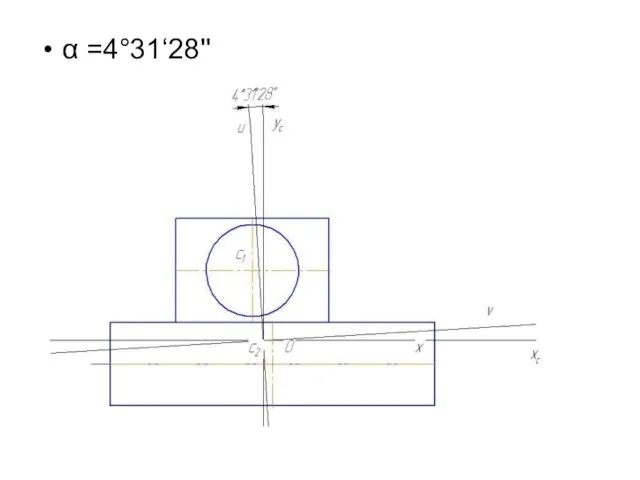
- 32. Построим главные оси системы:
- 33. Моменты инерции фигур относительно собственных осей: Ось X
- 34. Jxc = Jx1 +A1 *(y1 -yc )2 -Jx2 - A2 *(y2 -yc )2+ Jx3 + A3
- 35. Ось Y
- 36. Jyc = Jy1 +A1 *(x1 -xc )2 –Jy2 - A2 *(x2 -xc )2+ Jy3 + A3
- 37. Jxy2=A2 * (a2 -yc ) *(b2 -xc )=1256*(40.5-10.277)*(9-4.1)=186004,4 мм4 Jxy3=A3 * (a3 -yc ) *(b3 -xc
- 38. Определим угол поворота
- 39. α =4°31‘28''
- 40. Определим моменты инерции относительно главных осей:
- 43. Скачать презентацию



























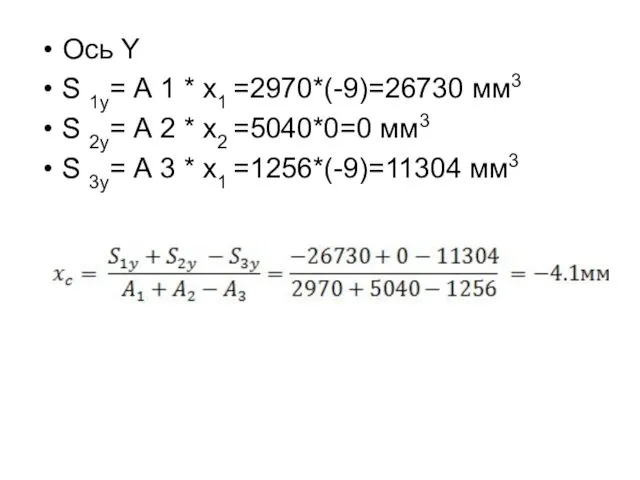









 Понятие дифференциала. Приложение дифференциала
Понятие дифференциала. Приложение дифференциала Многоугольники
Многоугольники Презентация к уроку в технологии деятельностного метода Тип урока: урок»открытия» новых знаний 5 класс Учитель математики
Презентация к уроку в технологии деятельностного метода Тип урока: урок»открытия» новых знаний 5 класс Учитель математики  Признак параллелограма
Признак параллелограма Решение задач по теме «Четырехугольники»
Решение задач по теме «Четырехугольники» Презентация на тему Комплексные числа
Презентация на тему Комплексные числа Линейные пространства со скалярным произведением
Линейные пространства со скалярным произведением Дробно-рациональные уравнения
Дробно-рациональные уравнения Неповні квадратні рівняння та алгоритми
Неповні квадратні рівняння та алгоритми Выборочное наблюдение
Выборочное наблюдение Степень с целым показателем. 9 класс. Екатеринбург. МОУ гимназия №13 Учитель Анкина Т.С.
Степень с целым показателем. 9 класс. Екатеринбург. МОУ гимназия №13 Учитель Анкина Т.С.  Вопросы к экзамену
Вопросы к экзамену Орнамент. Алгоритм построения орнамента. Черчение
Орнамент. Алгоритм построения орнамента. Черчение Корреляционно-регрессионный анализ в экономическом прогнозировании
Корреляционно-регрессионный анализ в экономическом прогнозировании Доли. Обыкновенные дроби
Доли. Обыкновенные дроби Геометрический смысл линейного неравенства
Геометрический смысл линейного неравенства Длина окружности и площадь круга. Тест
Длина окружности и площадь круга. Тест Презентация по математике "Единицы меры площади" - скачать бесплатно
Презентация по математике "Единицы меры площади" - скачать бесплатно Введение в эконометрику
Введение в эконометрику Построение графиков функций
Построение графиков функций Расстояние между скрещивающимися прямыми
Расстояние между скрещивающимися прямыми Решение задач и выражений. Урок №93
Решение задач и выражений. Урок №93 Построение сечений многогранников
Построение сечений многогранников Прямоугольный тетраэдр
Прямоугольный тетраэдр Действия с графиками. Васильева Екатерина ученица 11 «А» МОУ «Общеобразовательная гимназия № 6» г. Архангельск
Действия с графиками. Васильева Екатерина ученица 11 «А» МОУ «Общеобразовательная гимназия № 6» г. Архангельск Геометрические построения и приемы работы чертежными инструментами
Геометрические построения и приемы работы чертежными инструментами Расстояние от точки до прямой. Перпендикулярные прямые
Расстояние от точки до прямой. Перпендикулярные прямые Rehabilitation
Rehabilitation