Содержание
- 2. Определение обладающее свойствами сохранения углов и постоянства растяжений называется конформным отображением в точке z0 => б.м.
- 3. Основное определение. Непрерывное взаимно однозначное области g⊂ Z ↔ D ⊂ W, при котором в ∀z∈g
- 4. Теорема 20.1 Если f(z)∈C∞(g), однозначная и однолистная, и f ’(z)≠0, ∀z∈g, то Доказательство. Данное отображение f(z)
- 5. Теорема 20.2(обратная) Если , то f(z)∈C∞(g), однолистна, и f ’(z)≠0, ∀z∈g. Доказательство. , то f(z)- непрерывна,
- 6. Постоянство растяжений => Сохранение углов => ■ Замечание. Свойство f ’(z)≠0, ∀z∈g является следствием однолистности.
- 7. Теорема 20.3. Необходимым и достаточным условием конформного отображения является f(z)∈C∞(g), однозначна и однолистна в g. Доказательство.
- 8. Основные принципы конформных отображений. Принцип соответствия границ. Если f(z)∈C ∞( g ), g-односвязна и f(ξ): ∂g⬄Γ=∂D
- 9. Доказательство. Докажем, что f(z) однолистна в g, т.е. а) ∀w1∈D ∃! z1∈g : w1=f(z1); б) ∀w2∉D
- 10. Подсчитаем число нулей этих функций по принципу аргумента:
- 11. ■ Замечание. Если f(z)∈C∞(g\z0), z0- полюс первого порядка и f(ξ): ∂g↔Γ с изменением направления обхода, то
- 12. Обратная теорема. Если f(z): (D-ограничена), то f(z)∈C (∂ g ) и осуществляет непрерывное и взаимно-однозначное соответствие
- 13. Теорема Римана Основной закон конформных отображений g⊂ Z ; D ⊂ W Теорема Римана. Если g-
- 14. Теорема 20.4. Если g- односвязная g⊂ Z , ∂ g состоит более чем из одной так
- 15. Замечания 1) Пусть g⊂ Z ; D ⊂ W ∈ т. Римана Тогда ∃ξ=f(z): , f(z0)=
- 17. 2) Односвязность существенна! 3) Условия т. Римана можно заменить установлением соответствия 3-х точек ∂g трем точкам
- 18. п.4. Основные функции, используемые при конформных отображениях.
- 19. 1) Степенная w=f(z)=zn : область однолистности 0
- 20. f(z)=z2
- 23. 2) w=f(z)=1/z : область однолистности- вся комплексная плоскость.
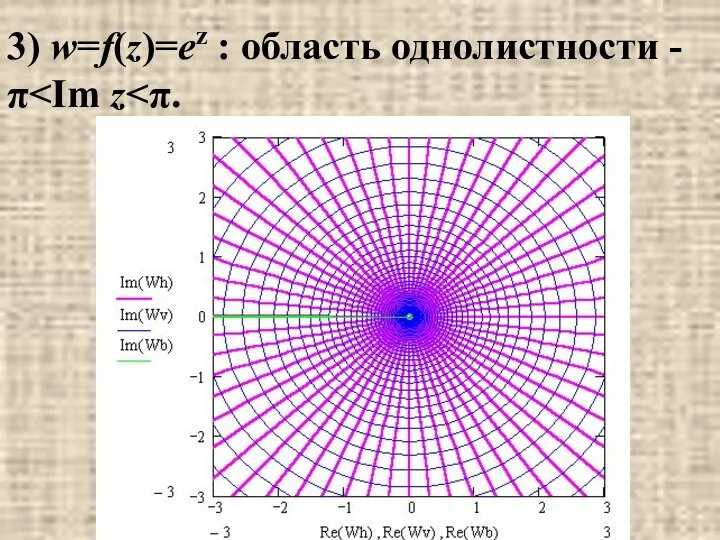
- 25. 3) w=f(z)=ez : область однолистности -π
- 27. Дробно-линейная функция (ДЛФ) 3 параметра, α≠β. , f '(z)≠0 для ∀z
- 28. 1) Геометрический смысл. повороты и растяжения, отражение от действительной оси, инверсия
- 29. 2) Заданием соответствия z1↔w1, z2↔w2, z3↔w3, ДЛФ определена однозначно, т.е. коэффициенты λ, α, β однозначно выражаются
- 30. Доказательство
- 32. Свойства дробно-линейной функции. 1) Круговое: A(x2+y2)+Bx+Cy+D=0; z=x+iy=1/ζ=1/(ξ+iη)= =ξ/(ξ2+η2)-iη/(ξ2+η2)=> x=ξ/(ξ2+η2), y= -η/(ξ2+η2) => A+Bξ-Cη+D(ξ2+η2)=0.
- 33. Задав zi↔wi, i=1,2,3 Окружность на плоскости однозначно определяется заданием 3-х точек.=> c сохранением направления обхода однозначно
- 34. Пример. z=1↔w= 0; z= i ↔w= 1; z= -1 ↔ w = ∞ ; w=λ(z-1)/(z+1); 1=λ(i-1)/(i+1)=>
- 35. Сохранение сопряженности точек. Сопряженные=> Сопряженные
- 36. Пример.
- 38. Скачать презентацию



























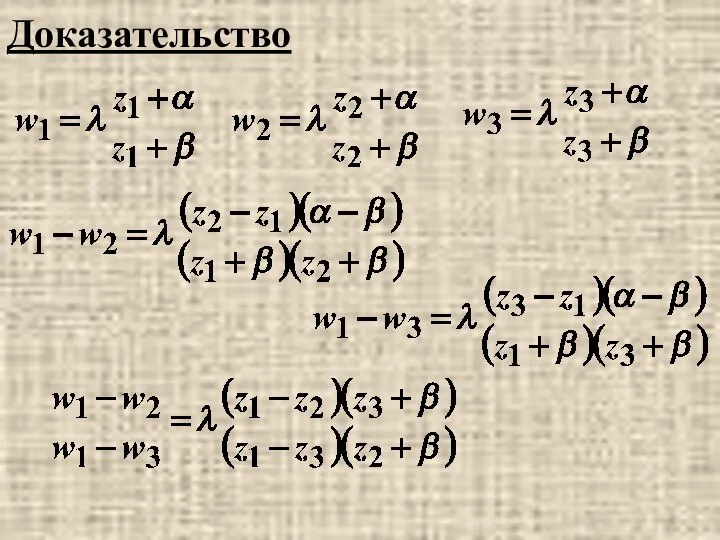



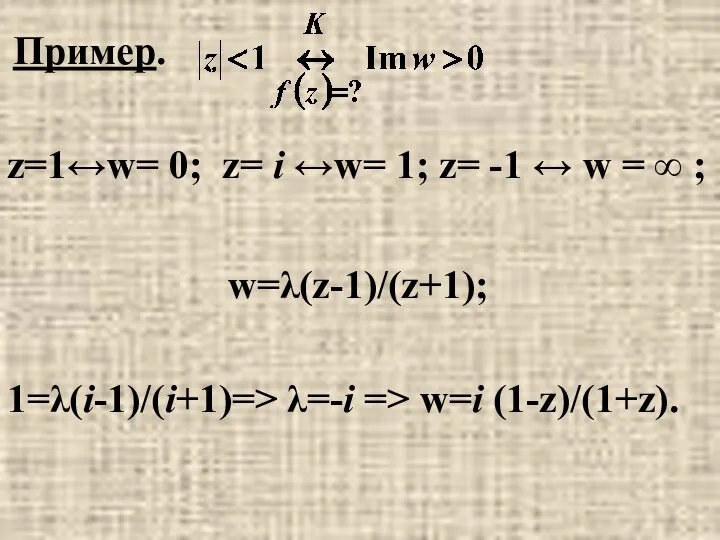


 Принципы статистического оценивания. Анализ данных
Принципы статистического оценивания. Анализ данных ТЕМА УРОКА: «СЛОЖЕНИЕ И ВЫЧИТАНИЕ ДЕСЯТИЧНЫХ ДРОБЕЙ». Урок-путешествие
ТЕМА УРОКА: «СЛОЖЕНИЕ И ВЫЧИТАНИЕ ДЕСЯТИЧНЫХ ДРОБЕЙ». Урок-путешествие Предварительная обработка экспериментальных данных
Предварительная обработка экспериментальных данных Рациональные выражения. 8 класс
Рациональные выражения. 8 класс Метрологическое обеспечение сертификации. (Лекция 1)
Метрологическое обеспечение сертификации. (Лекция 1) Решение иррациональных уравнений
Решение иррациональных уравнений 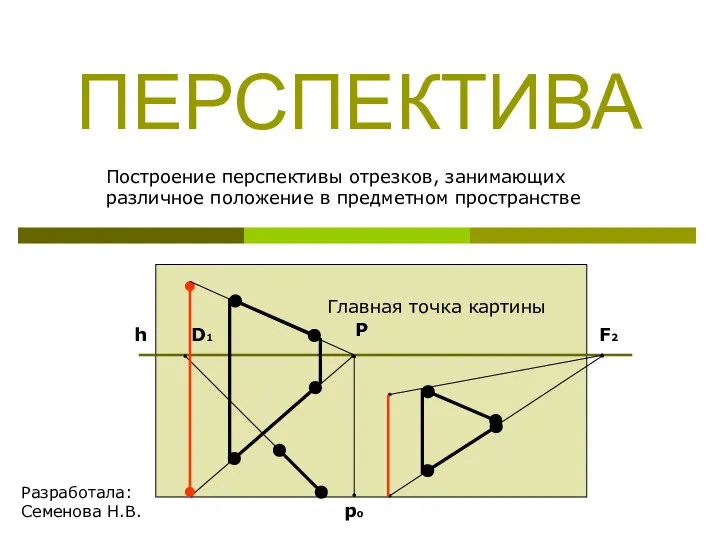 Построение перспективы отрезков, занимающих различное положение в предметном пространстве
Построение перспективы отрезков, занимающих различное положение в предметном пространстве Презентация на тему Умножение многозначного числа на двузначное число
Презентация на тему Умножение многозначного числа на двузначное число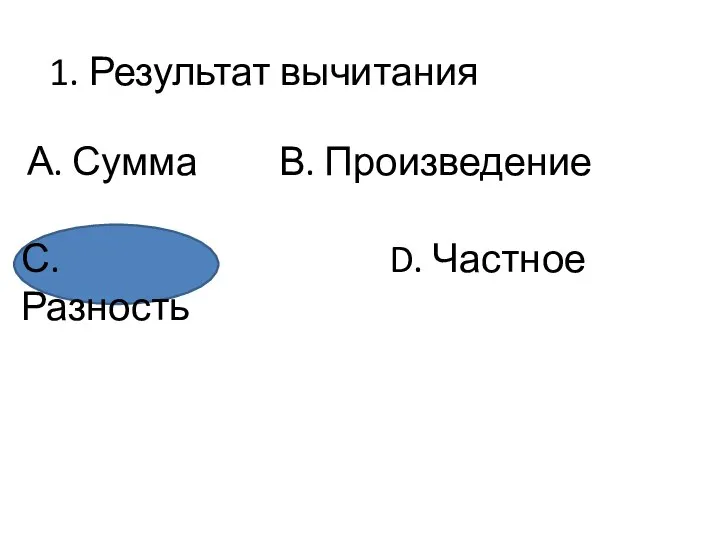 Игра
Игра Симметрия. Симметричные фигуры
Симметрия. Симметричные фигуры Нестандартные задачи как средство формирования исследовательских умений обучающихся в курсе алгебры 8 класса
Нестандартные задачи как средство формирования исследовательских умений обучающихся в курсе алгебры 8 класса Решение задач с составлением таблиц истинности
Решение задач с составлением таблиц истинности Тригонометрические формулы
Тригонометрические формулы Признаки подобия треугольников
Признаки подобия треугольников Синус и косинус суммы аргументов
Синус и косинус суммы аргументов Соотношения между сторонами и углами прямоугольного треугольника
Соотношения между сторонами и углами прямоугольного треугольника Математические диктанты для 8-х классов по геометрии
Математические диктанты для 8-х классов по геометрии Применение первого признака равенства треугольников к решению практических задач
Применение первого признака равенства треугольников к решению практических задач Взаимное пересечение поверхностей
Взаимное пересечение поверхностей Cложение и вычитание алгебраических дробей с разными знаменателями. 8 класс
Cложение и вычитание алгебраических дробей с разными знаменателями. 8 класс Вычислительная механика. Изопараметрические конечные элементы
Вычислительная механика. Изопараметрические конечные элементы Решение задач по теории вероятности
Решение задач по теории вероятности Интеллектуальная игра по математике
Интеллектуальная игра по математике Факторный анализ
Факторный анализ Презентация на тему 2 класс Математический диктант
Презентация на тему 2 класс Математический диктант Тригонометрические уравнения
Тригонометрические уравнения Решение задач по теме «Подобные слагаемые»
Решение задач по теме «Подобные слагаемые» Функциональная зависимость
Функциональная зависимость