Лекция 1 Векторы векторное произведение и т д-1

Векторное произведение. Определение. Свойства.

Определение. Упорядоченная тройка некомпланарных векторов называется правой, если из конца

Определение 1. Векторным произведением называется третий вектор , который удовлетворяет трем

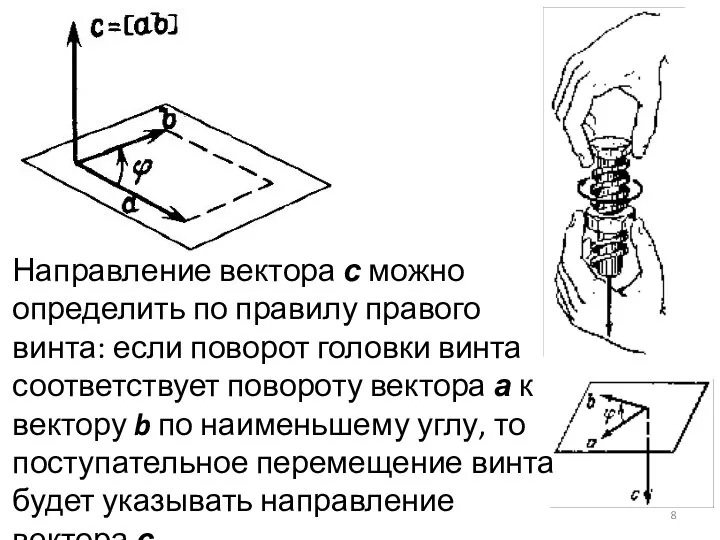
Направление вектора с можно определить по правилу правого винта: если поворот

Замечание: Определение 1 однозначно определяет вектор в том случае, если не

Доказательство
Необходимость. Пусть (по определению 1).
Достаточность . Пусть .
Из определения 1

Теорема 2. Модуль векторного произведения равняется площади параллелограмма, построенного на и

Алгебраические свойства векторного произведения
1) Антипереместительное
2) Сочетательное свойства относительно скаляра (ассоциативность)
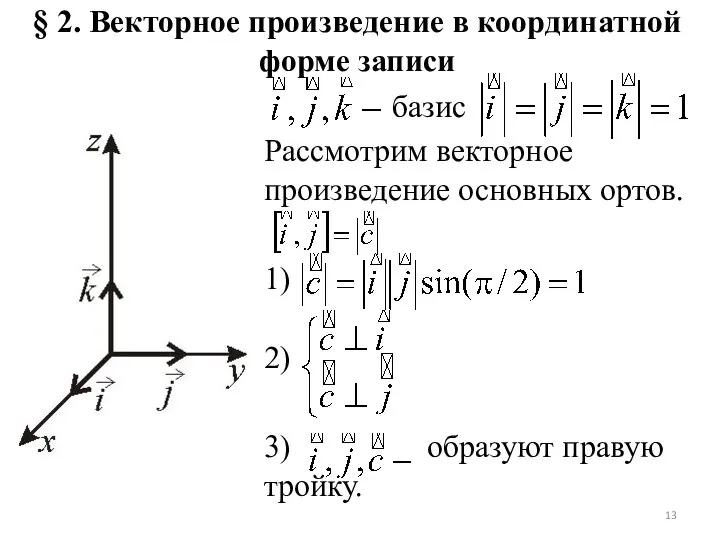
3)

§ 2. Векторное произведение в координатной форме записи

базис
Рассмотрим векторное

Итак
Пусть в прямоугольной декартовой системе координат XOYZ
или

По распределительному свойству и можно перемножать по правилу многочленов. По сочетательному свойству

Раскрывая символический определитель третьего порядка по элементам 1-ой строки мы получим

§ 3. Условие колинеарности двух векторов в координатной форме

Пусть
Значит все три

§ 4. Смешанное произведение трёх векторов
Определение. Смешанным или векторно-скалярным произведением

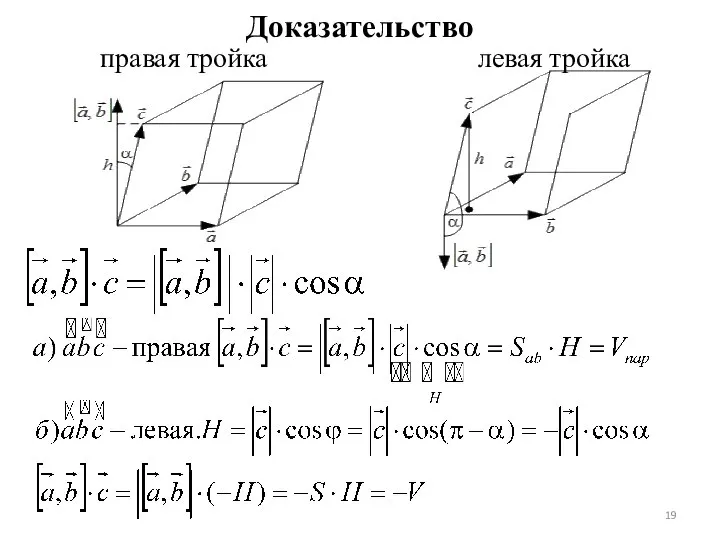
Доказательство

правая тройка левая тройка

То есть в смешанном произведении безразлично какие из векторов перемножаются векторно,

По определению 1:
ч.т.д.
Необходимость. Пусть
По опреде-
лению 1:
Ч.т.д.
Так как их
скалярное произведение =

§ 6. Смешанное произведение в координатной форме

Теорема. Если заданы в прямоугольной