Содержание
- 2. Содержание лекции
- 3. Ключевые понятия
- 4. Основные понятия и определения Матрицей называется таблица, состоящая из n строк и m столбцов. Таблица имеет
- 6. Обозначение матрицы Матрицы обозначаются заглавными латинскими буквами (A, B, A1, B1) или А={аij}n×m. Матрица, у которой
- 9. Действия над матрицами Две матрицы одинаковой размерности называются равными, если равны элементы, стоящие на одинаковых местах.
- 10. Суммой 2-х матриц одинаковой размерности называется матрица, элементы которой находят по правилу: А={аij}n×m, B={bij}n×m A+B=C={cij}n×m. cij=aij+bij
- 12. Для того чтобы матрицу умножить на число, надо каждый элемент матрицы умножить на это число: А={аij}n×m;
- 13. Если А={аij}n×m, B={bij}n×m, то разностью матриц А и В называется матрица C={cij}n×m, где cij=aij-bij.
- 14. Введём операцию умножения матрицы таким образом, чтобы выполнялось условие: Аn×p∙Вp×m=Сn×m.
- 16. Свойства операций над матрицами А+В=В+А А∙В≠В∙А α∙(А+В)= αА+ αВ А(В+С)=А∙В+А∙С (строго!)
- 17. 5) Если в матрице А строки заменить местами, то получим так называемую транспонированную матрицу. Если А
- 18. 6) Для квадратных матриц вычисляют определители матриц, которые обозначаются символами ΔА; |A|; ||A||; detA (детерминант), являющиеся
- 19. Обратная матрица Матрица А-1 называется обратной матрице А, если А-1∙А=А∙А-1=Е. Вывод 1: обратная матрица существует для
- 21. Квадратная матрица, у которой определитель отличен от 0, т.е. |А|≠0, называется невырожденной. В противном случае называется
- 22. Теорема о единственности обратной матрицы. Если матрица имеет обратную, то единственную.
- 23. Теорема о существовании обратной матрицы. Чтобы матрица имела обратную, необходимо и достаточно, чтобы она была квадратной
- 24. Алгоритм построения обратной матрицы 1) Убеждаемся, что матрица квадратная (для прямоугольных матриц нет обратных). 2) Вычисляем
- 25. 3) Если определитель не равен 0, то вычисляем алгебраические дополнения элементов матрицы. 4) Из алгебраических дополнений
- 27. Линейная зависимость и линейная независимость столбцов и строк
- 28. Столбцы называются линейно-независимыми, когда линейная комбинация равна 0 при всех α=0. Столбцы называются линейно-зависимыми, если линейная
- 29. Теорема. Столбцы линейно-зависимы, когда хотя бы один столбец является линейной комбинацией остальных. Теорема. Столбцы матрицы можно
- 30. Ранг матрицы Дана матрица размером n×m. Минором порядка r (Mr) называется определитель, составленный из элементов, стоящих
- 33. Минор порядка r называется базисным, если он отличен от 0, и миноры более высоких порядков равны
- 34. Нахождение ранга матрицы через миноры трудоёмкая операция. Существует алгоритм, позволяющий достаточно легко найти ранг и базисный
- 35. Теорема. Ранг матрицы равен максимальному числу линейно-зависимых столбцов матрицы. Максимальное число линейно-независимых строк равно максимальному числу
- 36. Теорема. Линейные преобразования столбцов или строк матрицы не меняют ранг матрицы. К линейным преобразованиям строк относятся
- 37. перестановка строк местами; прибавление к одной строке другой строки, умноженной на некоторое число; умножение строки на
- 38. Теорема. Ранг матрицы равен числу ненулевых строк (столбцов), полученных в результате применения элементарных преобразований, которые позволяют
- 40. Применим к матрице элементарные преобразования. Подчеркнём элементы, имеющие одинаковые индексы. Ниже или выше этих элементов будем
- 42. Вопросы и задания для самопроверки
- 43. Рекомендуемая литература
- 45. Скачать презентацию










































 Николай Иванович Лобачевский Подготовила : преподаватель математики Бурова Т.Н.
Николай Иванович Лобачевский Подготовила : преподаватель математики Бурова Т.Н.  Тригонометрические уравнения
Тригонометрические уравнения Кеңістіктегі тікбұрышты координаталар жүйесі
Кеңістіктегі тікбұрышты координаталар жүйесі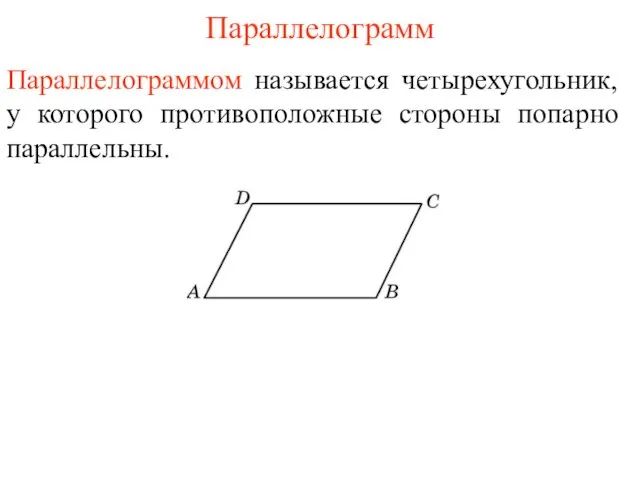 Параллелограмм. Свойства параллелограмма
Параллелограмм. Свойства параллелограмма Проверка умножения (3 класс)
Проверка умножения (3 класс) Подготовка к экзамену по начертательной геометрии
Подготовка к экзамену по начертательной геометрии Делимость чисел
Делимость чисел Раздел математики, изучающий количество комбинаций - комбинаторика
Раздел математики, изучающий количество комбинаций - комбинаторика Нерівності. Властивості раціональних чисел
Нерівності. Властивості раціональних чисел Использование информационных технологий на уроке математики как средство повышения его эффективности
Использование информационных технологий на уроке математики как средство повышения его эффективности Преобразование графиков функций. 8 класс
Преобразование графиков функций. 8 класс Презентация по математике "Длина окружности. Площадь круга. Практические применения" - скачать
Презентация по математике "Длина окружности. Площадь круга. Практические применения" - скачать  Аналитическое задание фигур
Аналитическое задание фигур Скачать презентацию Умножение
Скачать презентацию Умножение  Применение метода интервалов для решения неравенств
Применение метода интервалов для решения неравенств Приглашаем на неделю математики!
Приглашаем на неделю математики!  Теорема Пифагора
Теорема Пифагора Тема: Отношения между ПОНЯТИЯМИ На дом: учебник стр 45-50 (учить)
Тема: Отношения между ПОНЯТИЯМИ На дом: учебник стр 45-50 (учить) Взаимное расположение графиков линейных функций
Взаимное расположение графиков линейных функций Қазақстандағы математика
Қазақстандағы математика Презентация по математике "«Отрицательные числа» 6 класс" - скачать бесплатно
Презентация по математике "«Отрицательные числа» 6 класс" - скачать бесплатно Дробные числительные
Дробные числительные Презентация на тему Четырехугольники решение задач
Презентация на тему Четырехугольники решение задач Основы математической обработки информации. Вариационные ряды и их характеристики. (Лекция 1)
Основы математической обработки информации. Вариационные ряды и их характеристики. (Лекция 1) Правила округления и представления результатов измерений
Правила округления и представления результатов измерений Степенные ряды Лекции12, 13, 14
Степенные ряды Лекции12, 13, 14  Математика. Множители. Произведение
Математика. Множители. Произведение Признаки подобия треугольников
Признаки подобия треугольников