Содержание
- 2. Основные сведения о матрицах
- 3. Понятие матрицы Матрицей размера m×n называется прямоугольная таблица чисел, содержащая m строк и n столбцов. Обозначение
- 4. Запись матриц В общем виде В сокращенной форме
- 5. Пример
- 6. Виды матриц Определение: Матрица любого размера называется нулевой или нуль-матрицей, если все ее элементы равны нулю.
- 7. Виды матриц Матрица, размерности: 1×n называется матрицей-строкой или вектором-строкой m×1 называется матрицей-столбцом или вектором-столбцом
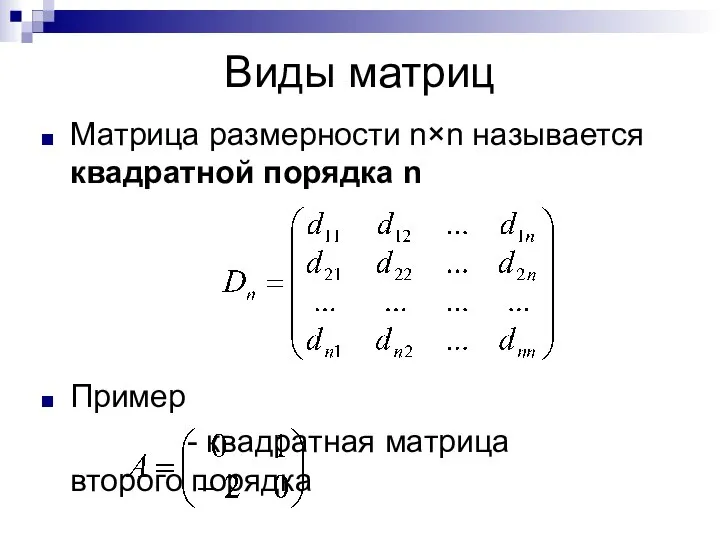
- 8. Виды матриц Матрица размерности n×n называется квадратной порядка n Пример - квадратная матрица второго порядка
- 9. Диагональ матрицы Элементы матрицы, у которых номер столбца равен номеру строки (i=j), называются диагональными и составляют
- 10. Виды квадратных матриц Квадратная матрица, у которой все недиагональные элементы равны нулю, называется диагональной матрицей. Пример:
- 11. Виды квадратных матриц Если у диагональной матрицы порядка n все диагональные элементы равны 1, матрица называется
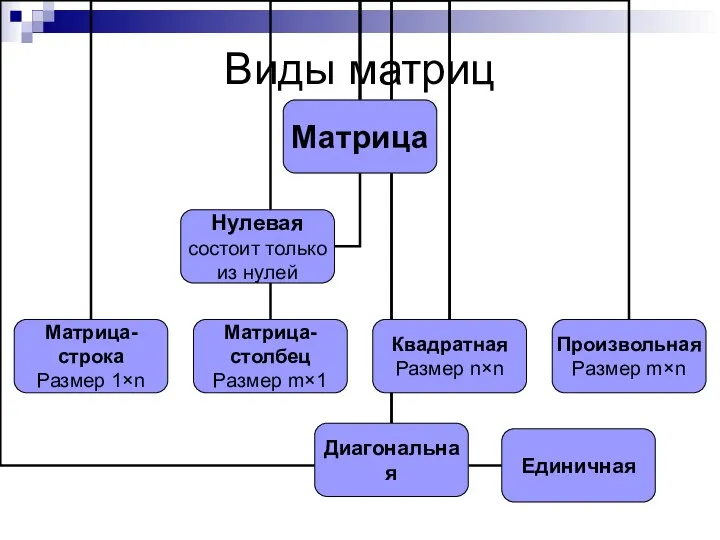
- 12. Виды матриц
- 13. Операции над матрицами
- 14. Операции над матрицами Умножение матрицы на число Сложение матриц Вычитание матриц Умножение матриц Возведение в степень
- 15. Умножение матрицы на число Выполнимо для любых матриц и любых чисел Производится поэлементно Правило: Пример:
- 16. Сложение матриц Выполнимо только для матриц одинаковой размерности Производится поэлементно Правило: Пример:
- 17. Вычитание матриц Выполнимо только для матриц одинаковой размерности Производится поэлементно Правило: или Пример:
- 18. Умножение матриц Выполнимо если число столбцов первого множителя равно числу строк второго Правило: Примеры:
- 19. Возведение в степень Выполнимо для квадратных матриц Правила: Пример:
- 20. Транспонирование Выполнимо для любой матрицы Обозначение: АТ или А' Правило: поменять строки на столбцы с сохранением
- 21. Определители квадратных матриц
- 22. Зачем нужны определители? Понятие определителя возникло в связи с проблемой решения системы n-линейных алгебраических уравнений. Например,
- 23. системы двух линейных уравнений: или трех линейных уравнений:
- 24. Первые идеи, которые привели к созданию теории определителей и применению их к решению систем линейных алгебраических
- 25. В XVIII столетии вопросами теории определителей и систем линейных алгебраических уравнений занимались: Г. Крамер, французские ученые
- 26. П. С. Лаплас (1749-1827) Доказал теорему о разложении определителя по строкам(столбцам), а также ряд важных свойств
- 27. Ж. Л. Лагранж (1736-1813) Ввел обозначение для определителя, рассмотрел алгебраические дополнения, доказал теоремы замещения и аннулирования.
- 28. К. Ф. Гаусс (1777-1855) Рассмотрел произведение определителей второго порядка, ввел название «детерминант».
- 29. Н. И. Лобачевский (1792-1856) Предложил свой собственный способ решения систем линейных уравнений. Впервые включил теорию определителей
- 30. Определитель матрицы Любой квадратной матрице ставится в соответствие по определенному закону некоторое число, называемое определителем или
- 31. Определитель первого порядка Определяется по формуле: при А=(а11) ∆1=а11 Пример: А=(-5) ∆1= ∆А = - 5
- 32. Определитель второго порядка Определяется формулой: Пример:
- 33. Определитель третьего порядка Определяется формулой
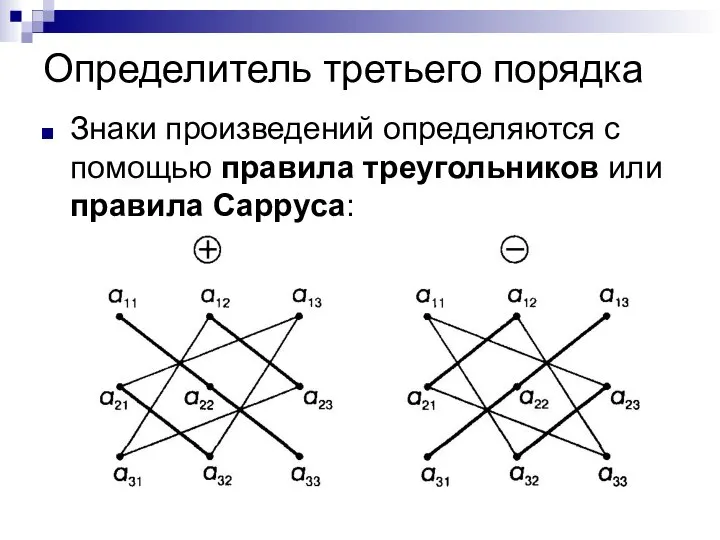
- 34. Определитель третьего порядка Знаки произведений определяются с помощью правила треугольников или правила Сарруса:
- 35. Определитель n-го порядка Определителем матрицы А n-го порядка называется алгебраическая сумма n! произведений n-го порядка элементов
- 36. Минор Рассмотрим квадратную матрицу Аn Минором называется определитель (n-1)-го порядка, полученный вычеркиваем из матрицы А i-й
- 37. Алгебраическое дополнение Алгебраическим дополнением называется минор , взятый со знаком , т.е. Пример Матрица, составленная из
- 38. Теорема Лапласа Определитель равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения: - разложение
- 39. Теорема Лапласа (пример) Вычислить Решение:
- 40. Свойства определителей При транспонировании ∆ не меняется. При перестановке двух строк ∆ меняет знак. ∆=0 если:
- 41. Свойства определителей Определитель треугольной матрицы равен произведению ее диагональных элементов. Определитель диагональной матрицы равен произведению ее
- 42. Способы вычисления определителей Перебором всевозможных произведений (по определению); Разложением по строке или столбцу (по теореме Лапласа);
- 43. Обратная матрица Обозначение: А-1–обратная для матрицы А Определение: Матрицей А-1, обратной к данной квадратной матрице А,
- 44. Обратимость матрицы Если определитель квадратной матрицы равен нулю (∆А=0), матрица называется вырожденной. Если определитель отличен от
- 45. Алгоритм нахождения обратной матрицы Вычислить ∆А. Если ∆А=0, то А-1 не существует. Если ∆А≠0, найти алгебраические
- 46. Нахождение обратной матрицы (пример) Найти матрицу, обратную к Решение: 1. ∆А = -1∙1 - 2∙0 =
- 47. Нахождение обратной матрицы (пример) 4. 5. Проверка: Ответ:
- 48. Ранг матрицы Определение: Рангом матрицы называется наивысший порядок отличных от нуля миноров этой матрицы. Обозначение: rang
- 50. Скачать презентацию












































 Слагаемые, сумма 1 класс - Презентация по математике
Слагаемые, сумма 1 класс - Презентация по математике Таблиця ділення на 3. Збери букет для Попелюшки
Таблиця ділення на 3. Збери букет для Попелюшки Приемы устных вычислений. Формирование навыков устных вычислений на уроках математики
Приемы устных вычислений. Формирование навыков устных вычислений на уроках математики Подготовка к ЕГЭ по математике. Решение задач В12
Подготовка к ЕГЭ по математике. Решение задач В12 Старинные задачи. История возникновения арифметических задач
Старинные задачи. История возникновения арифметических задач Умножение двузначного числа на однозначное
Умножение двузначного числа на однозначное Понятие движения
Понятие движения Сумма углов треугольника. Теорема
Сумма углов треугольника. Теорема Умножение десятичной дроби на натуральное число. 5 класс
Умножение десятичной дроби на натуральное число. 5 класс Задачи на построение
Задачи на построение Многогранники
Многогранники Умножение десятичных дробей. Урок математики 6 класс
Умножение десятичных дробей. Урок математики 6 класс Последовательности: путешествие вглубь веков
Последовательности: путешествие вглубь веков Делимость натуральных чисел
Делимость натуральных чисел Азбука
Азбука Математика. Исправляем ошибки
Математика. Исправляем ошибки Одночлен и его стандартный вид_
Одночлен и его стандартный вид_ Математический вечер "Ох, уж эта математика"
Математический вечер "Ох, уж эта математика" Функционально замкнутые классы. Специальные классы булевых функций
Функционально замкнутые классы. Специальные классы булевых функций Свойства и способы вычисления двойных интегралов. Двойной интеграл в прямоугольных декартовых и полярных координатах. Лекция 15
Свойства и способы вычисления двойных интегралов. Двойной интеграл в прямоугольных декартовых и полярных координатах. Лекция 15 История числа Пи
История числа Пи Связь между компонентами и результатом умножения
Связь между компонентами и результатом умножения Обернена задача
Обернена задача Золотое сечение и числа Фибоначчи
Золотое сечение и числа Фибоначчи Творческая работа по математике. Табличное умножение (учебник Н.Б. Истомина «Гармония»)
Творческая работа по математике. Табличное умножение (учебник Н.Б. Истомина «Гармония») Площадь треугольника. 9 класс
Площадь треугольника. 9 класс Линейная функция и ее график
Линейная функция и ее график Теория вероятности в ЕГЭ . По математике примеры и решения
Теория вероятности в ЕГЭ . По математике примеры и решения