Содержание
- 2. Литература Монаков А.А. Основы математического моделирования радиотехнических систем. Учебное пособие. – СПб.: ГУАП, 2005. – 100с.
- 3. Литература Дьяконов В. П. MATLAB 7.*/R2006/R2007: Самоучитель. – М.: ДМК Пресс, 2008. – 768 с.: ил.
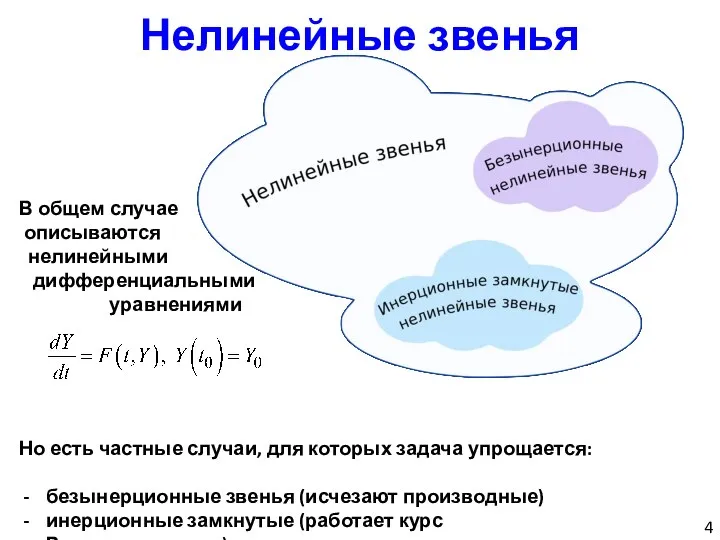
- 4. Нелинейные звенья В общем случае описываются нелинейными дифференциальными уравнениями Но есть частные случаи, для которых задача
- 5. Нелинейные звенья Таблица − Типовые звенья радиоавтоматики
- 6. Нелинейные звенья Таблица − Типовые звенья радиоавтоматики (продолжение)
- 7. Безынерционные звенья Дано звено Производит нелинейное преобразование входного сигнала В общем случае вида: Моделирование сводится к:
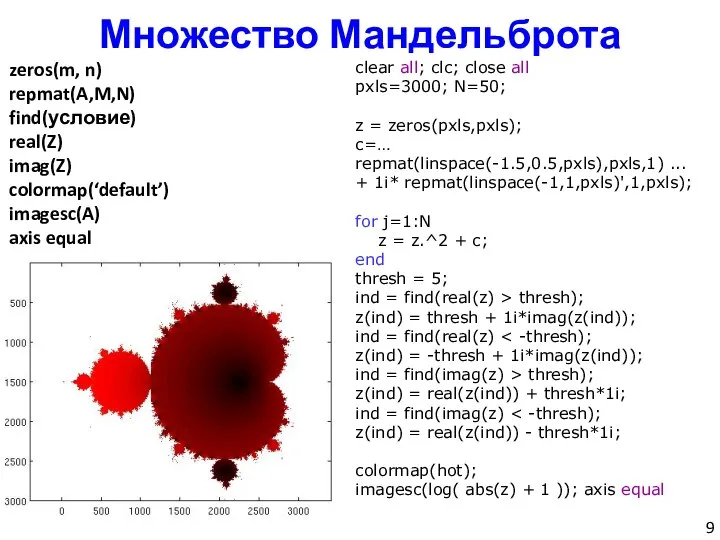
- 8. Множество Мандельброта – множество точек с на комплексной плоскости, для которых последовательность сходится |zn| Фрактал —
- 9. Множество Мандельброта clear all; clc; close all pxls=3000; N=50; z = zeros(pxls,pxls); c=… repmat(linspace(-1.5,0.5,pxls),pxls,1) ... +
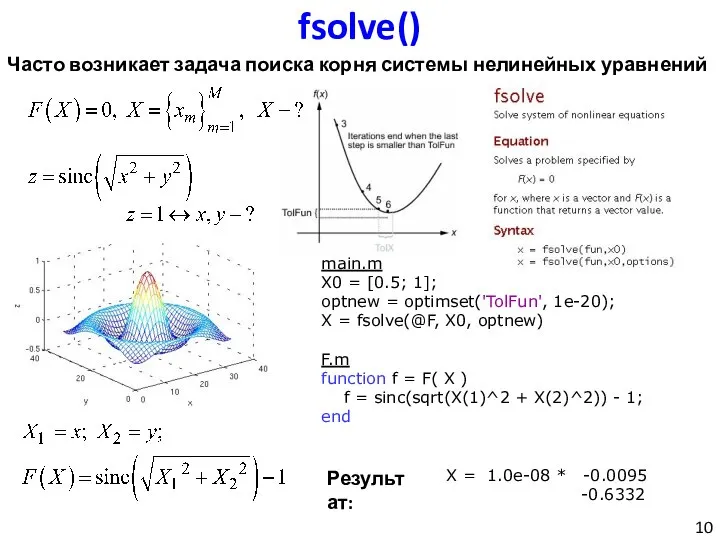
- 10. fsolve() Часто возникает задача поиска корня системы нелинейных уравнений main.m X0 = [0.5; 1]; optnew =
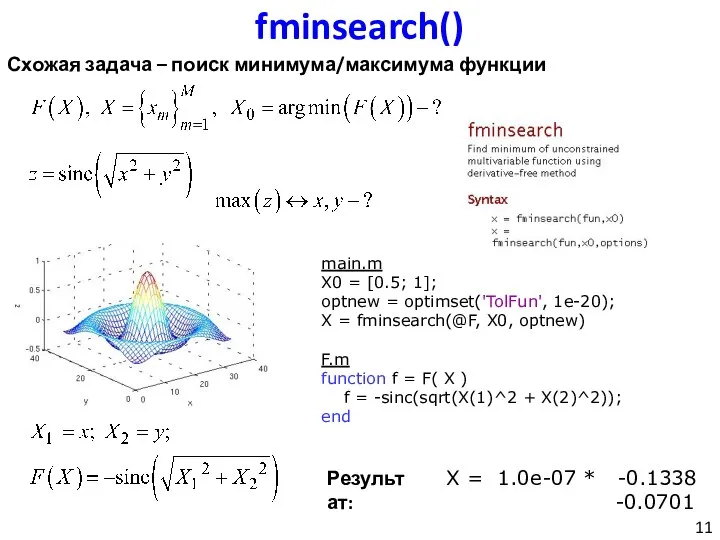
- 11. fminsearch() Схожая задача – поиск минимума/максимума функции main.m X0 = [0.5; 1]; optnew = optimset('TolFun', 1e-20);
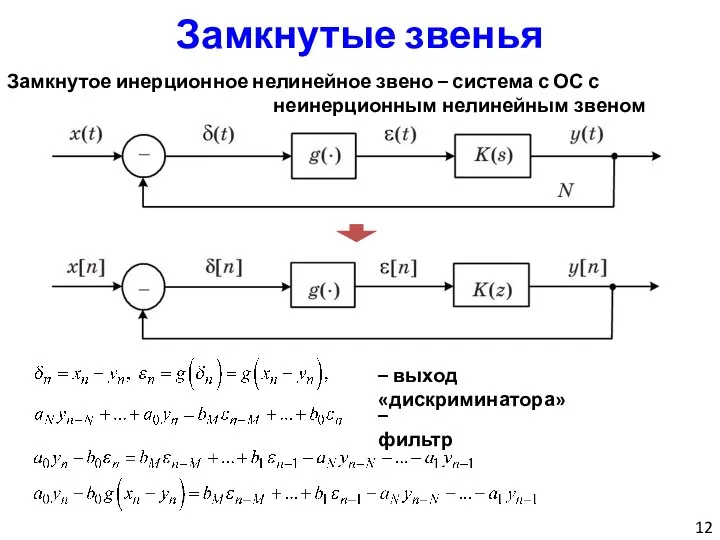
- 12. Замкнутые звенья Замкнутое инерционное нелинейное звено – система с ОС с неинерционным нелинейным звеном – выход
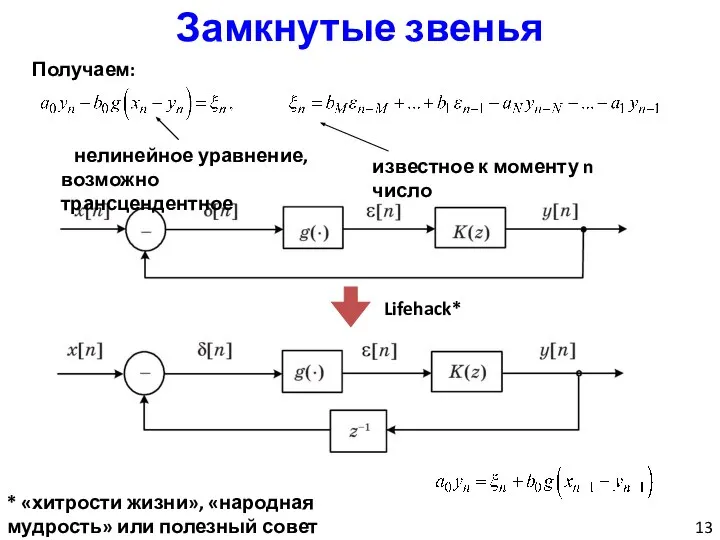
- 13. Замкнутые звенья Получаем: Lifehack* нелинейное уравнение, возможно трансцендентное известное к моменту n число * «хитрости жизни»,
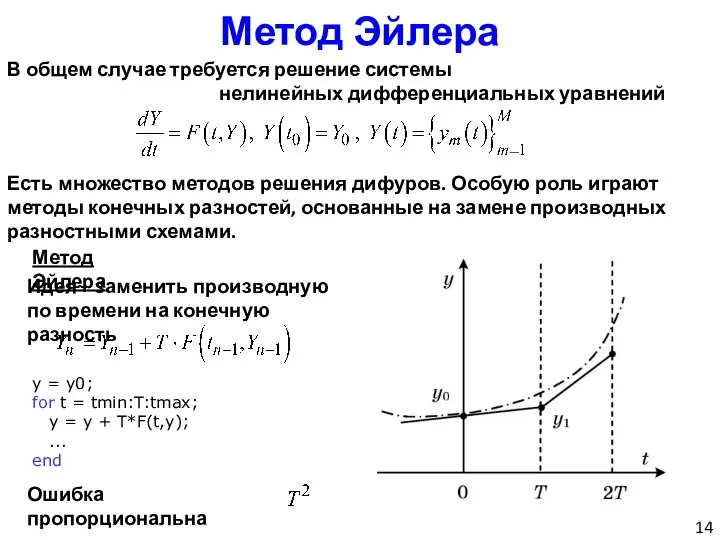
- 14. Метод Эйлера В общем случае требуется решение системы нелинейных дифференциальных уравнений Есть множество методов решения дифуров.
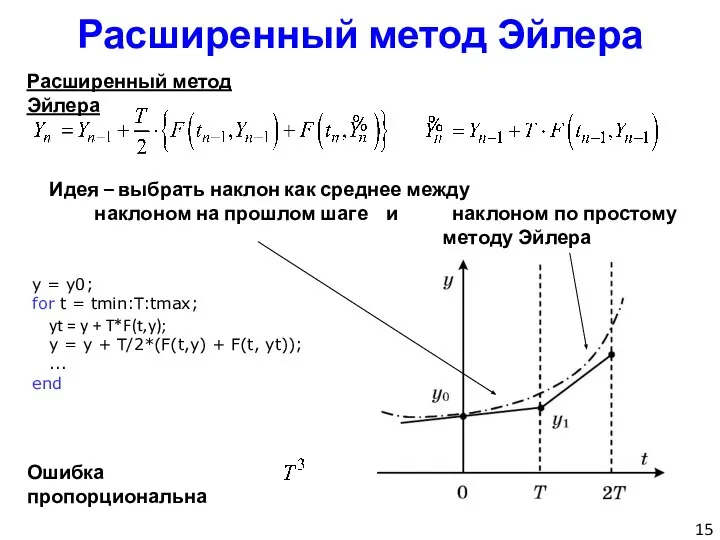
- 15. Расширенный метод Эйлера Расширенный метод Эйлера Идея – выбрать наклон как среднее между наклоном на прошлом
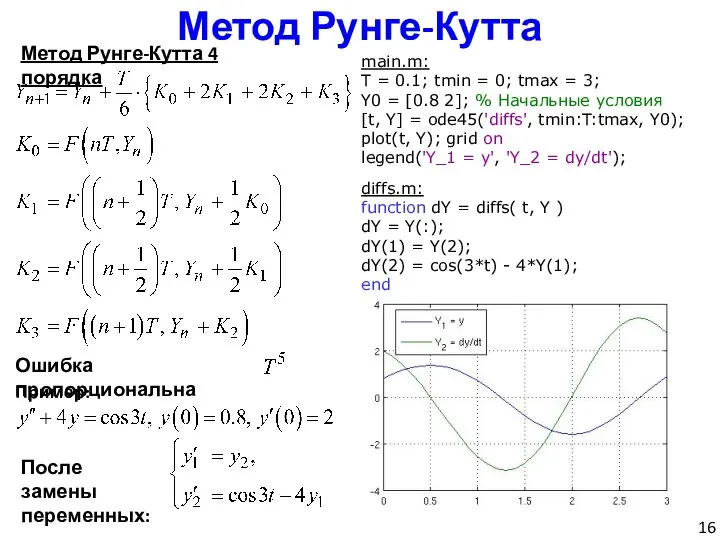
- 16. Метод Рунге-Кутта Метод Рунге-Кутта 4 порядка Ошибка пропорциональна Пример: После замены переменных: main.m: T = 0.1;
- 17. Решатели • ode45 – одношаговые явные методы Рунге Кутта 4 го и 5 го порядков. Использовать
- 18. Аттрактор Лоренца Описывается системой уравнений: clear all; clc; close all % Начальные условия Y0 = [10;10;10];
- 19. Аттрактор Лоренца
- 20. Аттрактор Лоренца Изменим на 1% начальные условия: Y0 = [10;10;10] * (1+1/100);
- 22. Скачать презентацию








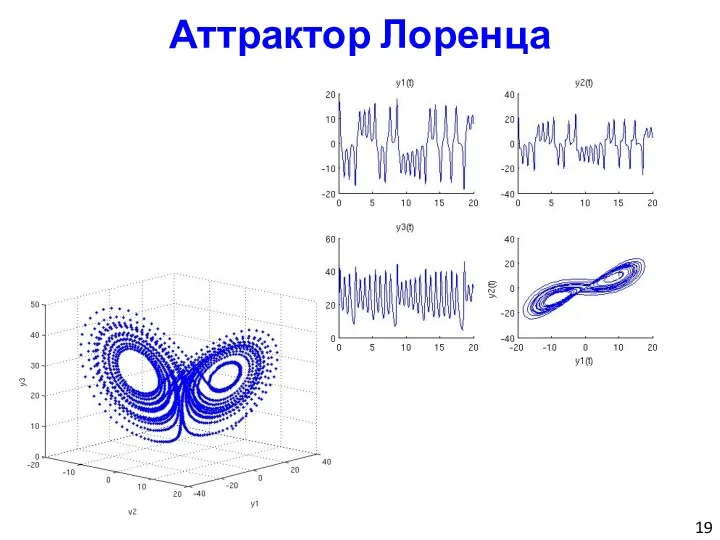
![Аттрактор Лоренца Изменим на 1% начальные условия: Y0 = [10;10;10] * (1+1/100);](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/769578/slide-19.jpg)
 Интеграл. Определенный интеграл. Свойства. Примеры. Применение определенного интеграла для нахождения длин, площадей и объемов
Интеграл. Определенный интеграл. Свойства. Примеры. Применение определенного интеграла для нахождения длин, площадей и объемов Правильные и неправильные дроби. 5 класс
Правильные и неправильные дроби. 5 класс Объём шара
Объём шара Из истории математики
Из истории математики Признаки подобия треугольников. Решение задач
Признаки подобия треугольников. Решение задач Интерактивный тест по математике. Решаем задачи с Буратино (3 класс)
Интерактивный тест по математике. Решаем задачи с Буратино (3 класс) Теорема Пифагора
Теорема Пифагора Презентация по математике "Сравнение отрезков и углов" - скачать бесплатно
Презентация по математике "Сравнение отрезков и углов" - скачать бесплатно Тузулер мен жазықтықтардын арақашықтығы
Тузулер мен жазықтықтардын арақашықтығы Округление десятичных чисел
Округление десятичных чисел Зарождение алгебры
Зарождение алгебры Муниципальное общеобразовательное учреждение средняя общеобразовательная школа №4 имени Владимира Бурова
Муниципальное общеобразовательное учреждение средняя общеобразовательная школа №4 имени Владимира Бурова Различные варианты сопряжения фигур
Различные варианты сопряжения фигур Число и цифра 6
Число и цифра 6 Прямая и обратная пропорциональности Учитель математики ГБОУ ЦО № 354 Лодзь О.В.
Прямая и обратная пропорциональности Учитель математики ГБОУ ЦО № 354 Лодзь О.В. Умножение и деление.Задачи
Умножение и деление.Задачи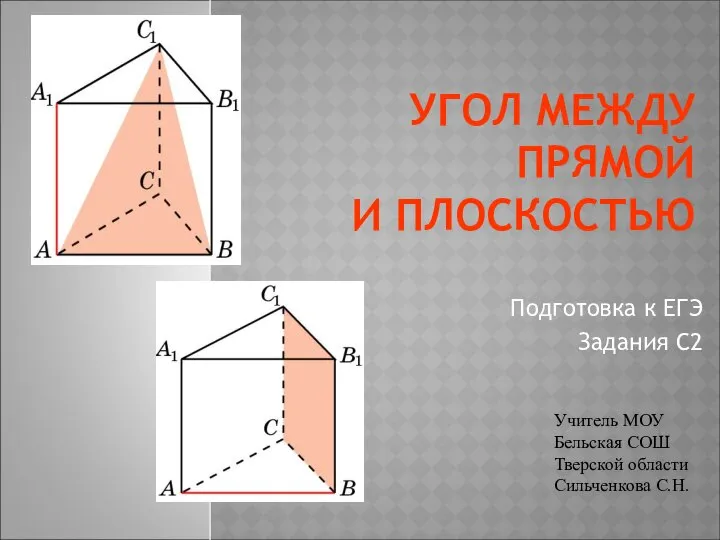 Угол между прямой и плоскостью
Угол между прямой и плоскостью Площадь треугольника
Площадь треугольника Функции. Игра «Счастливый случай»
Функции. Игра «Счастливый случай» Определители. Вычисление определителей высших порядков. Свойства определителей. Алгебраические дополнения и миноры
Определители. Вычисление определителей высших порядков. Свойства определителей. Алгебраические дополнения и миноры Площі бічної та повної поверхонь циліндра
Площі бічної та повної поверхонь циліндра Сравнительный анализ методов вычисления позиционных характеристик чисел в системе остаточных классов
Сравнительный анализ методов вычисления позиционных характеристик чисел в системе остаточных классов Нахождение площади фигур и объемов тел
Нахождение площади фигур и объемов тел Дисциплина: Современное проектирование зданий и сооружений. Проверки с использованием метода частных коэффициентов
Дисциплина: Современное проектирование зданий и сооружений. Проверки с использованием метода частных коэффициентов Решение некоторых нестандартных задач по алгебре. 9 класс
Решение некоторых нестандартных задач по алгебре. 9 класс Математика и искусство
Математика и искусство Презентация по математике Неравенства
Презентация по математике Неравенства Нахождение дроби от числа
Нахождение дроби от числа