Обыкновенные дифференциальные уравнения

Август 12, 2022

Главная
Математика
Обыкновенные дифференциальные уравнения

Содержание

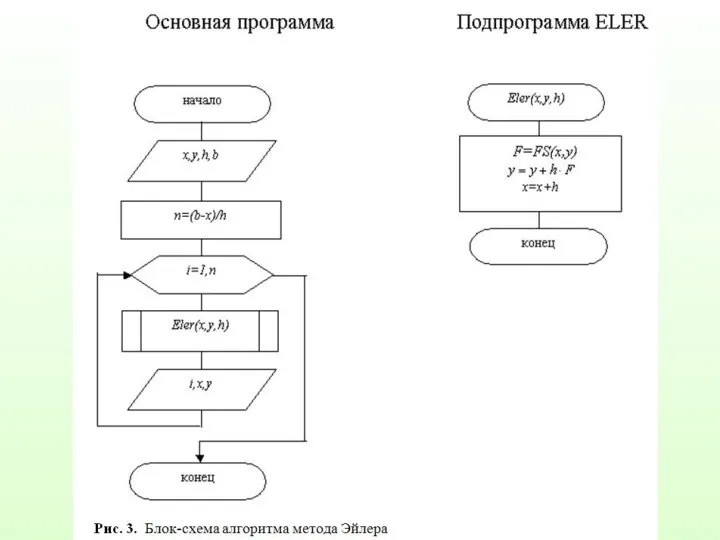
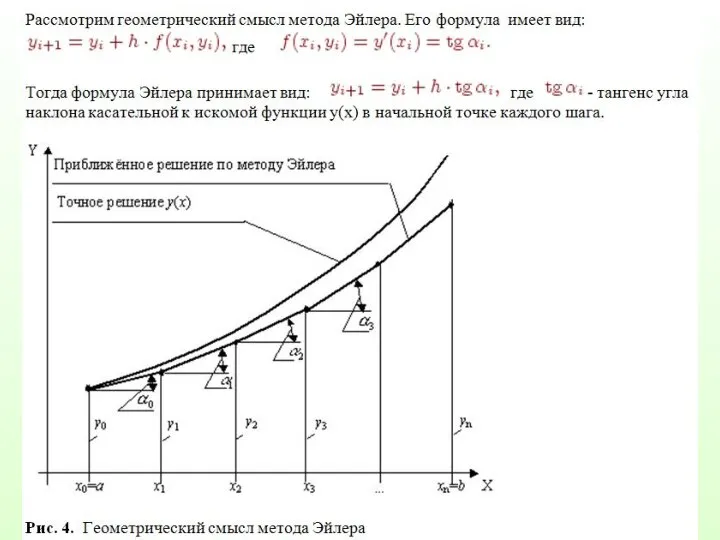
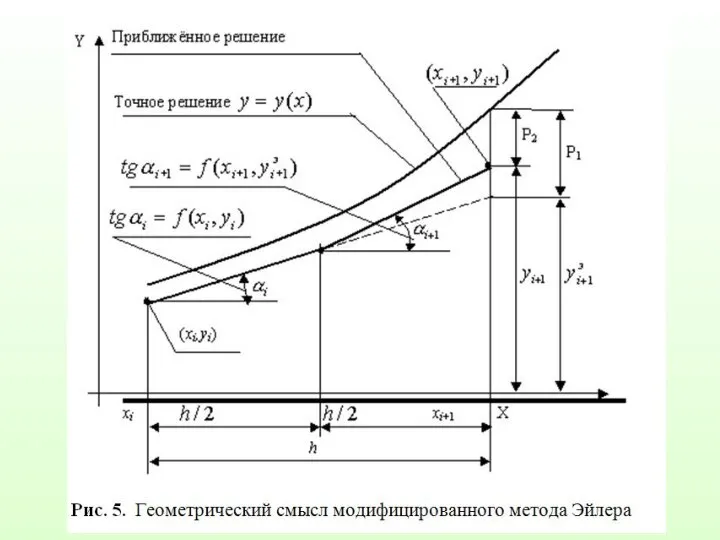
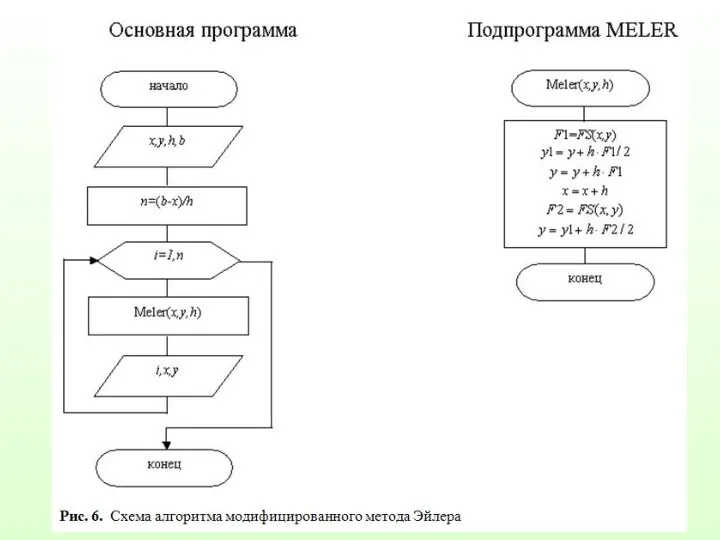
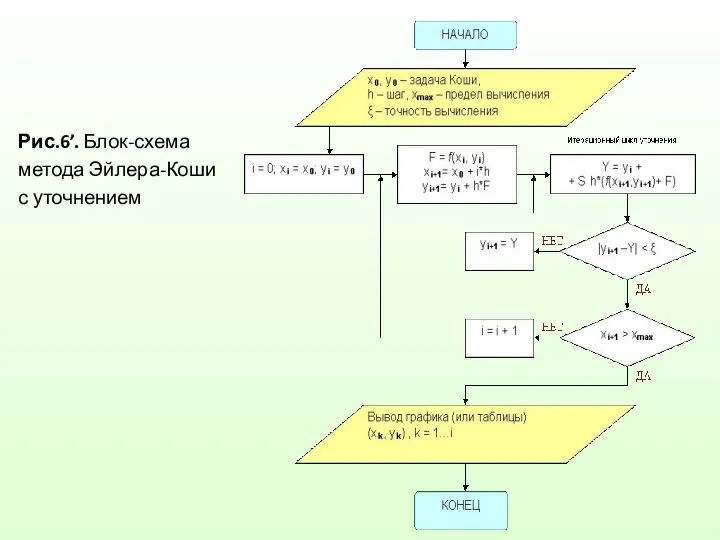
23. Рис.6’. Блок-схема метода Эйлера-Коши с уточнением
24. y(3) (xi)
25. yi
38. Решение дифференциальных уравнений в MATLAB Для решения дифференциальных уравнений и систем в MATLAB предусмотрены следующие функции
39. Все функции возвращают: массив Т - координаты узлов сетки, в которых ищется решение; матрицу X, i-й
40. Для решения системы с небольшим числом жёсткости можно использовать функцию ode23t, а для грубой оценки подобных
41. %примеры аналитического решения обыкновенных Data_sheet1.m %дифференциальных уравнений с помощью функции %MATLAB - dsolve %пример №1 (u'=au)
42. Пример: В М-файле с именем pr7.m пишем: function f=pr7(x,y) f=cos(x+y)+(3/2)*(x-y); end Потом в командном окне вызываем
43. Пример: Необходимо реализовать метод Рунге-Кутта 4 порядка и решить задачу Коши для предложенной системы дифференциальных уравнений:
44. Пример. % Решить задачу Коши методом Эйлера и оценить погрешность. % Введём функцию f = inline('y-t');
46. Скачать презентацию

Слайд 2

Слайд 3

Слайд 4

Слайд 5

Слайд 6

Слайд 7

Слайд 8

Слайд 9

Слайд 10

Слайд 11

Слайд 12

Слайд 13

Слайд 14

Слайд 15

Слайд 16

Слайд 17

Слайд 18

Слайд 19

Слайд 20

Слайд 21

Слайд 22

Слайд 23

Рис.6’. Блок-схема
метода Эйлера-Коши
с уточнением

Слайд 24

y(3) (xi)

Слайд 25

yi

Слайд 26

Слайд 27

Слайд 28

Слайд 29

Слайд 30

Слайд 31

Слайд 32

Слайд 33

Слайд 34

Слайд 35

Слайд 36

Слайд 37

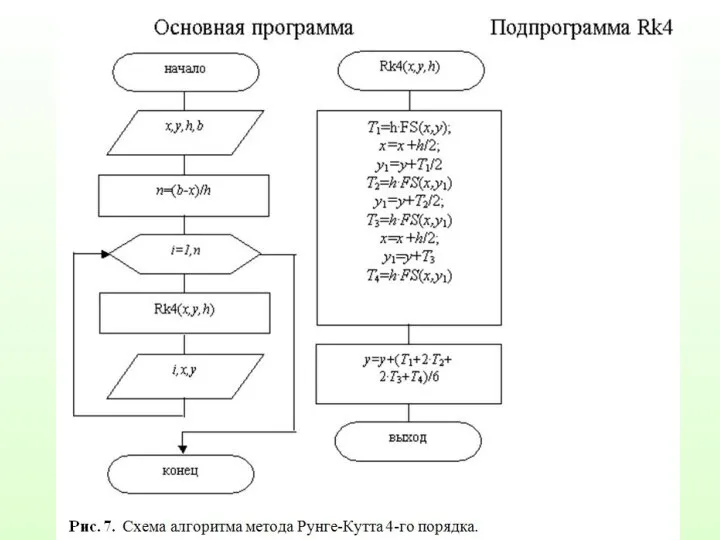
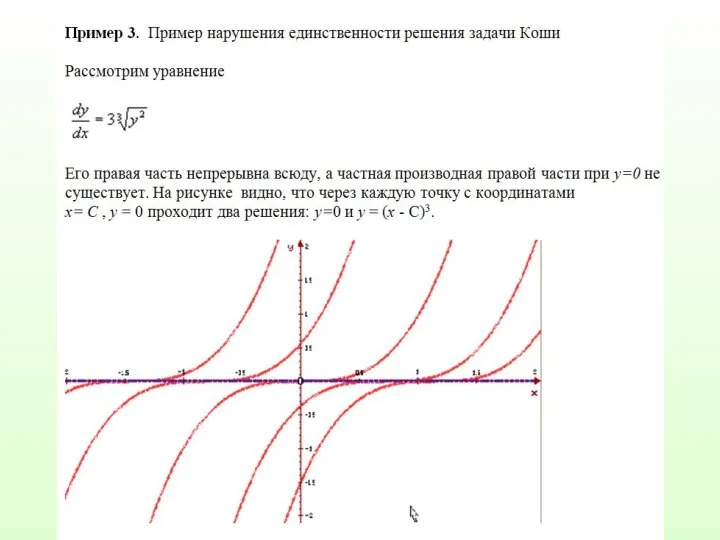
Слайд 38

Решение дифференциальных уравнений в MATLAB
Для решения дифференциальных уравнений и систем в

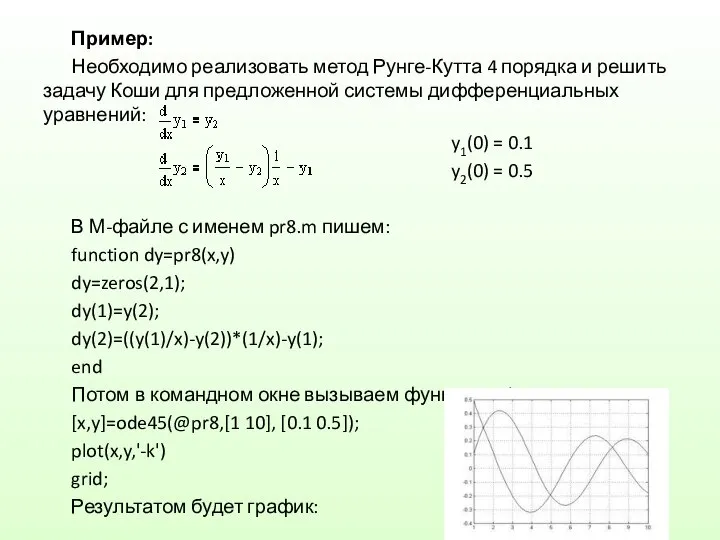
MATLAB предусмотрены следующие функции ode45(f, interval, X0 [, options]), ode23(f, interval, X0 [, options]), ode113(f, interval, X0 [, options]), ode15s(f, interval, X0 [, options]), ode23s(f, interval, X0 [, options]), ode23t (f, interval, X0 [,options]) и ode23tb(f, interval, X0 [, options]).
Входными параметрами этих функций являются:
f - вектор-функция для вычисления правой части уравнения системы уравнений;
interval - массив из двух чисел, определяющий интервал интегрирования дифференциального уравнения или системы;
Х0 - вектор начальных условий системы дифференциальных уравнений;
options - параметры управления ходом решения дифференциального уравнения или системы.

Слайд 39

Все функции возвращают:
массив Т - координаты узлов сетки, в которых ищется

решение;
матрицу X, i-й столбец которой является значением вектор-функции решения в узле Тi.
В функции ode45 реализован метод Рунге-Кутта 4-5 порядка точности, в функции ode23 также реализован метод Рунге-Кутта, но 2-3 порядка, а функция ode113 реализует метод Адамса.
Для решения жёстких систем предназначены функция ode15s, в которой реализован метод Гира, и функция ode23s, реализующая метод Розенброка. Для получения более точного решения жёсткой системы лучше использовать функцию ode15s.

Слайд 40

Для решения системы с небольшим числом жёсткости можно использовать функцию ode23t,

а для грубой оценки подобных систем служит функция ode23tb.
Символьное решение обыкновенных дифференциальных уравнений произвольного порядка осуществляет функция dsolve
r = dsolve('eq1,eq2,...', 'cond1,cond2,...‘,'v')
В листинге Data_sheet1.m приведен код программы, иллюстрирующей использование функции dsolve в MATLAB, которая даёт точное решение обыкновенных дифференциальных уравнений произвольного порядка.
MATLAB решил все семь дифференциальных уравнений, при этом последнее уравнение он не смог разрешить относительно зависимой переменной y, о чём и доложил.

Слайд 41

%примеры аналитического решения обыкновенных Data_sheet1.m
%дифференциальных уравнений с помощью функции
%MATLAB - dsolve
%пример

№1 (u'=au)
expl1=dsolve('Du=a*u','x')
%пример №2 (u'=u^2)
expl2=dsolve('Du=u^2','x')
%пример №3 (u''-g=0)
expl3=dsolve('D2u-g=0','x')
%пример №4 (u''+q^2u=0)
expl4=dsolve('D2u+q^2*u=0','x')
%пример №5 (u''-(3/4)x^(-2)u=0)
expl5=dsolve('D2u-(3/4)*x^(-2)*u=0','x')
%пример №6 (u'=f(x))
expl6=dsolve('Du=f(x)','x')
%пример №7 (u'=(u-x)/(u+x))
expl7=dsolve('Du=(u-x)/(u+x)','x')

Слайд 42

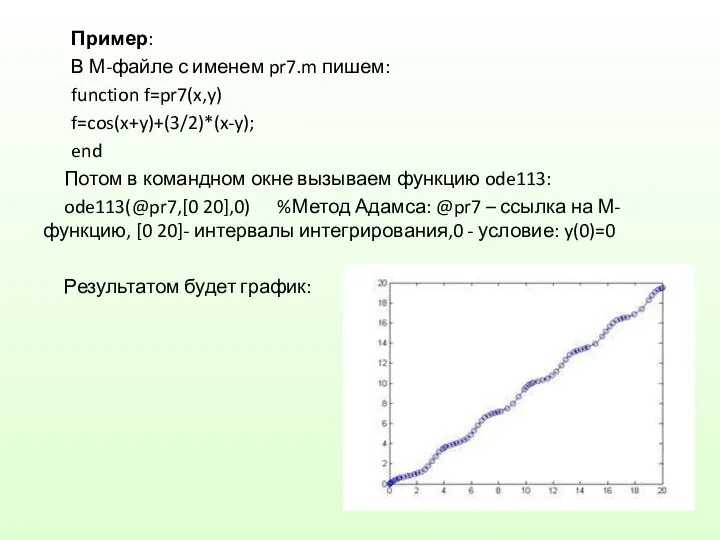
Пример:
В М-файле с именем pr7.m пишем:
function f=pr7(x,y)
f=cos(x+y)+(3/2)*(x-y);
end
Потом в командном окне вызываем

функцию ode113:
ode113(@pr7,[0 20],0) %Метод Адамса: @pr7 – ссылка на М-функцию, [0 20]- интервалы интегрирования,0 - условие: y(0)=0
Результатом будет график:

Слайд 43

Пример:
Необходимо реализовать метод Рунге-Кутта 4 порядка и решить задачу Коши для

предложенной системы дифференциальных уравнений:
y1(0) = 0.1
y2(0) = 0.5
В М-файле с именем pr8.m пишем:
function dy=pr8(x,y)
dy=zeros(2,1);
dy(1)=y(2);
dy(2)=((y(1)/x)-y(2))*(1/x)-y(1);
end
Потом в командном окне вызываем функцию ode45:
[x,y]=ode45(@pr8,[1 10], [0.1 0.5]);
plot(x,y,'-k')
grid;
Результатом будет график:

Слайд 44

Пример.
% Решить задачу Коши методом Эйлера и оценить погрешность. % Введём функцию f

= inline('y-t');
% Начальные условия y0 = 1.5;
% Точное решение ye = dsolve('Dy=y-t','y(0)=1.5');
% Приближённое решение по методу Эйлера, t=0..1 n = 100; h = 1 / n; y = []; t0 = 0; for i=1:n y(end+1) = y0; y0 = y0 + h * f(t0, y0); t0 = t0 + h; end
% Найдём погрешность решения t = linspace(0, 1, n); dy = max(abs(y - subs(ye, t)))
>> dy = 0.0301

Обыкновенные дифференциальные уравнения

Содержание

Рис.6’. Блок-схема метода Эйлера-Коши с уточнением

y(3) (xi)

yi

Решение дифференциальных уравнений в MATLABДля решения дифференциальных уравнений и систем в

Все функции возвращают:массив Т - координаты узлов сетки, в которых ищется

Для решения системы с небольшим числом жёсткости можно использовать функцию ode23t,

%примеры аналитического решения обыкновенных Data_sheet1.m%дифференциальных уравнений с помощью функции%MATLAB - dsolve%пример

Пример:В М-файле с именем pr7.m пишем:function f=pr7(x,y)f=cos(x+y)+(3/2)*(x-y);endПотом в командном окне вызываем

Пример:Необходимо реализовать метод Рунге-Кутта 4 порядка и решить задачу Коши для

Пример.% Решить задачу Коши методом Эйлера и оценить погрешность. % Введём функцию f

Похожие презентации