Содержание
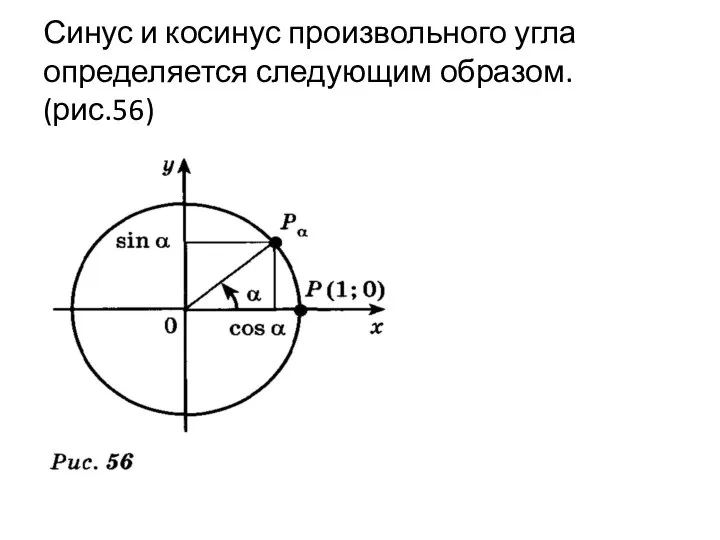
- 2. Синус и косинус произвольного угла определяется следующим образом. (рис.56)
- 3. Определение 1. Синус угла а называется ордината точки, получиной поворотом точки (1;0) вокруг начала координат на
- 4. Например, при повороте точки (1;0) на угол 2/π, т.е угол 90°, получается точка (0;1). Родина точки
- 6. Задача 1 найтиsin (-π) и cos (-π ). Точка (1;0) при повороте на угол -π перейдёт
- 7. Эти точки получаются из точки (1;0)поворотом на углы 0, π, 2π, 3π и т.д., а также
- 9. Скачать презентацию





 Свойство углов треугольника
Свойство углов треугольника  Принцип ортогонального сжатия
Принцип ортогонального сжатия Электронно-образовательные ресурсы к учебнику математики 3 класса, часть 2 (автор Н. Б. Истомина) для фронтальной работы с интер
Электронно-образовательные ресурсы к учебнику математики 3 класса, часть 2 (автор Н. Б. Истомина) для фронтальной работы с интер Числа
Числа Площади геометрических фигур
Площади геометрических фигур Задачи на взвешивание
Задачи на взвешивание Второй признак равенства треугольников
Второй признак равенства треугольников Ряды с положительными членами
Ряды с положительными членами Понятие логарифма. Свойства логарифмов
Понятие логарифма. Свойства логарифмов Неравенства и их решения
Неравенства и их решения Площадь квадрата
Площадь квадрата Правильные и неправильные дроби. Смешанные числа
Правильные и неправильные дроби. Смешанные числа Построение графиков, содержащих выражения под знаком модуля
Построение графиков, содержащих выражения под знаком модуля Введение в численные методы. Лекция 1, часть 1
Введение в численные методы. Лекция 1, часть 1 Вычитание (Помоги Буратино исправить ошибки)
Вычитание (Помоги Буратино исправить ошибки) Положительные и отрицательные числа
Положительные и отрицательные числа Аттестационная работа. Площадь треугольника. Урок математики в 5 классе
Аттестационная работа. Площадь треугольника. Урок математики в 5 классе Второй признак равенства треугольников
Второй признак равенства треугольников Освобождение от иррациональности в знаменателе
Освобождение от иррациональности в знаменателе Модуль числа
Модуль числа Цена, количество, стоимость
Цена, количество, стоимость Площадь треугольника
Площадь треугольника Симметрия относительно точки
Симметрия относительно точки Подготовка к ЕГЭ по математике. Решение задач В5
Подготовка к ЕГЭ по математике. Решение задач В5 Решение тестовых задач на движение (подготовка к ЕГЭ)
Решение тестовых задач на движение (подготовка к ЕГЭ) Пропорциональные отрезки (метрические соотношения) в прямоугольном треугольнике
Пропорциональные отрезки (метрические соотношения) в прямоугольном треугольнике Математика. Теория вероятностей
Математика. Теория вероятностей Дом дружбы народов. II региональный турнир по ментальной арифметике. Ижевск 2018
Дом дружбы народов. II региональный турнир по ментальной арифметике. Ижевск 2018