Основные понятия теории графов

Впервые понятие «граф» ввел в 1936 г. венгерский математик Денни Кёниг.

Леонард Эйлер
(1707 – 1783)

Графы

Задача
о кенигсбергских мостах

Граф – совокупность двух множеств G = , где V

Ориентированный граф (орграф)
- это граф, у которого на линиях, соединяющих вершины,

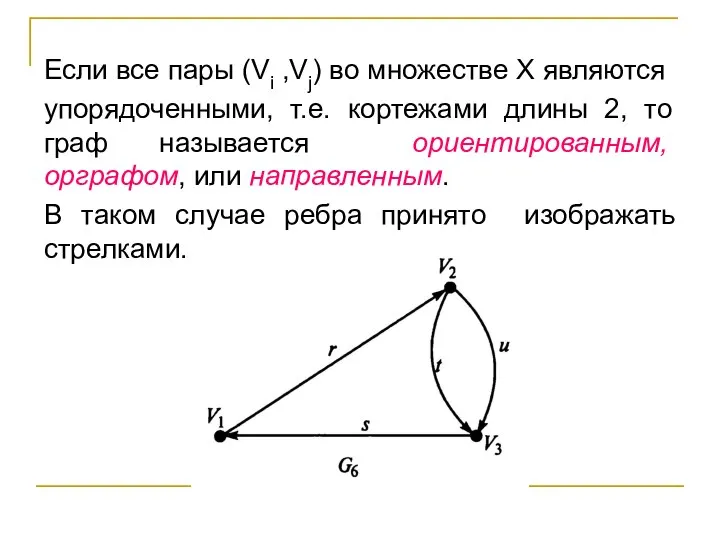
Если все пары (Vi ,Vj) во множестве X являются
упорядоченными, т.е.

Началом ребра называется вершина, указанная в кортеже первой, концом — вторая

Неориентированный граф

Ориентированный граф

Смешанный граф

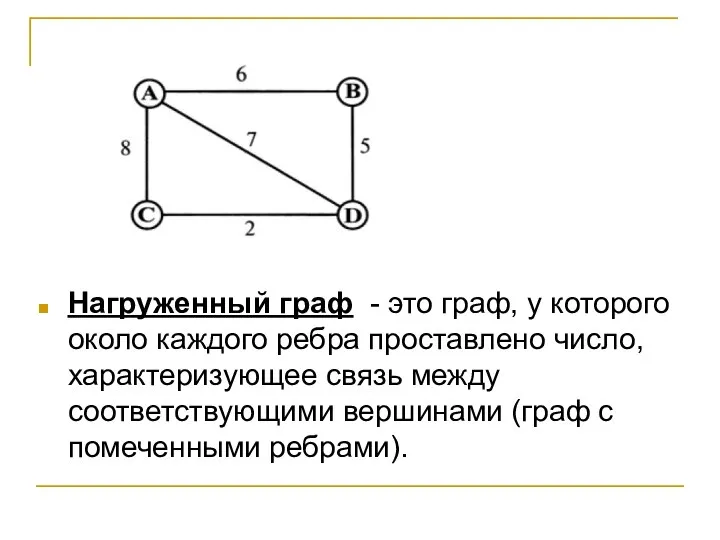
Нагруженный граф - это граф, у которого около каждого ребра проставлено

Сеть- это орграф, у которого около каждого ребра проставлено число, характеризующее

Определение.
Вершина графа, не принадлежащая ни одному ребру называется изолированной.
Пример.
Вершина

Определение.
Вершина А графа Г, принадлежащая одному ребру, называется висячей.
Пример
Вершины

Смежные вершины – это две вершины, соединенные ребром; ребро инцидентно этим

Примеры графов:
со смежными вершинами полный

Примеры графов:
со смежными ребрами с петлей

Записать:
смежные вершины:
смежные ребра:

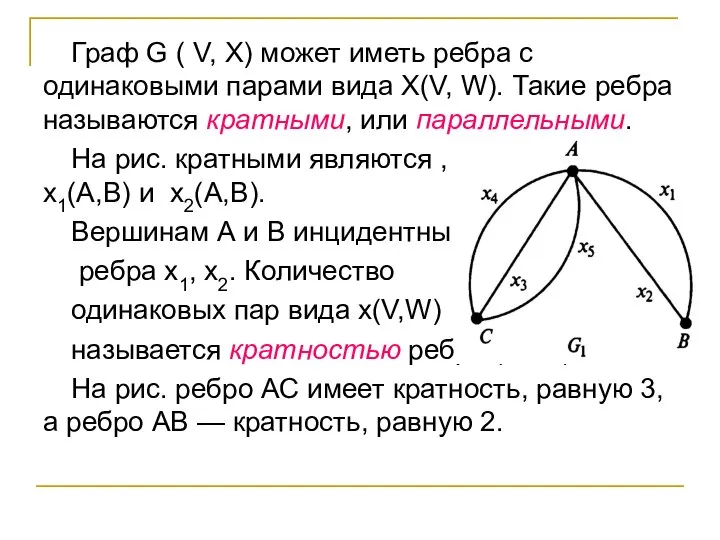
Граф G ( V, X) может иметь ребра с одинаковыми парами

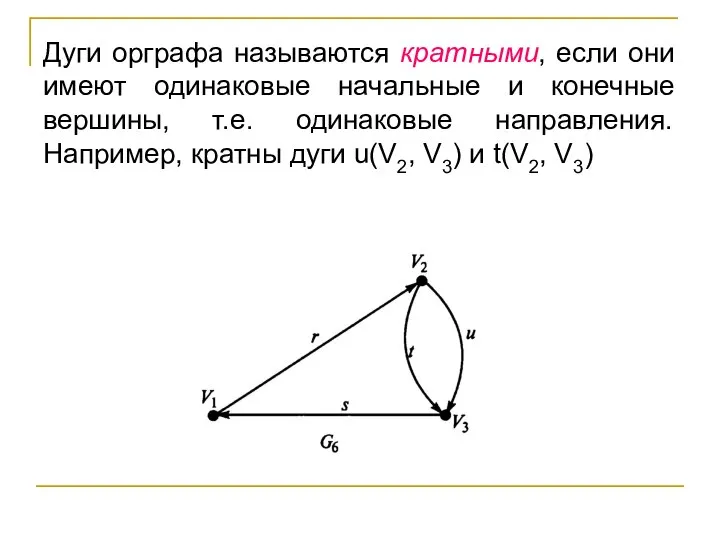
Дуги орграфа называются кратными, если они имеют одинаковые начальные и конечные

Простой граф – это н-граф без петель и без кратных ребер.
Турнир

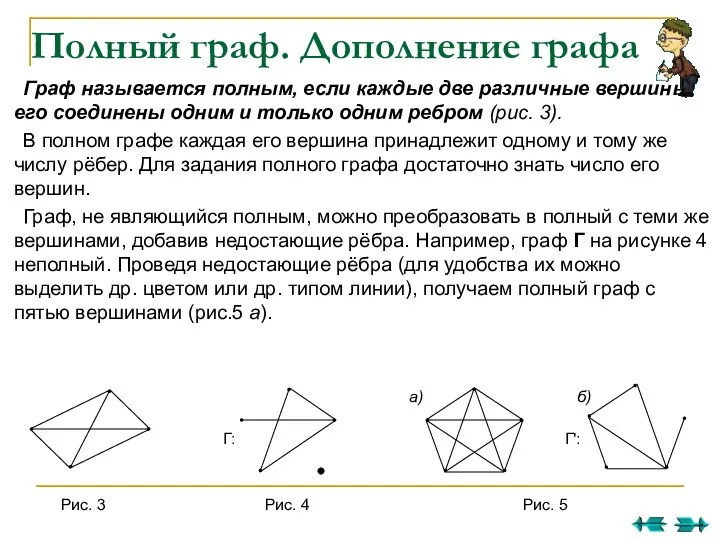
Полный граф. Дополнение графа

Граф называется полным, если каждые две различные вершины

Дополнение графа

Вершины графа Г и рёбра, которые добавлены, тоже образуют граф.

Дополнением графа G(V, X) называется граф
с теми же вершинами

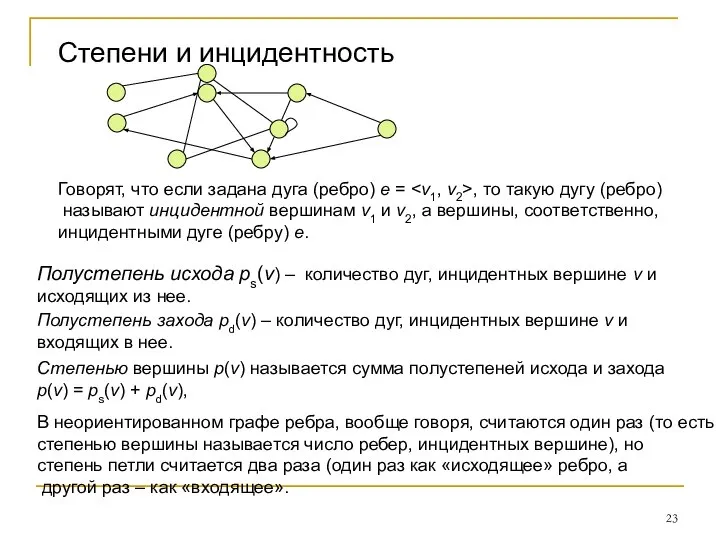
Степени и инцидентность

Говорят, что если задана дуга (ребро) e =

Число ребер, инцидентных вершине А, называется степенью этой вершины и обозначается

Граф G4 содержит четыре вершины:
V= (A,В, С, D)
и шесть

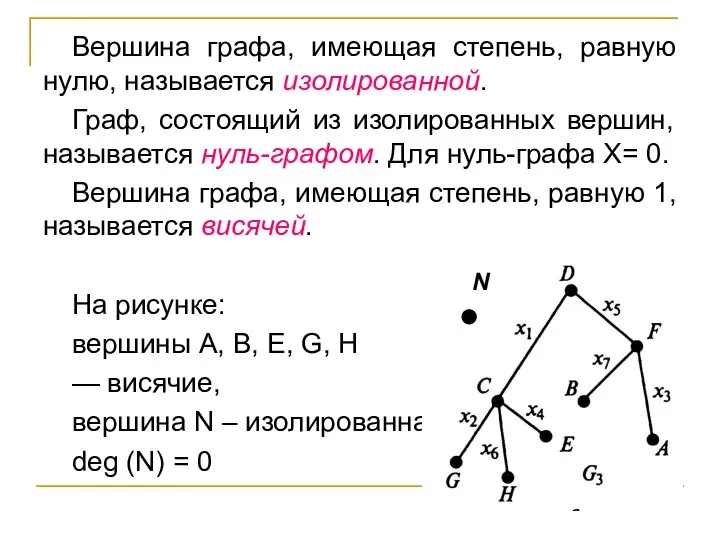
Вершина графа, имеющая степень, равную нулю, называется изолированной.
Граф, состоящий из

Граф G называется полным, если любые две его различные вершины соединены

Набор степеней графа – это последовательность степеней его вершин в неубывающем

Свойства степеней:

1) Для любого графа
сумма степеней вершин равна удвоенному количеству ребер
2)

Пример:

Может ли в государстве, в котором из каждого города выходят

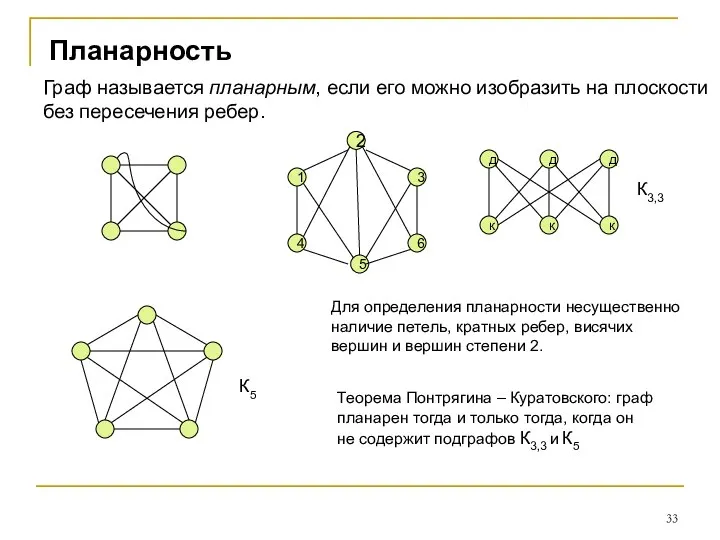
Планарность

Граф называется планарным, если его можно изобразить на плоскости
без пересечения ребер.

1

3

4

5

6

д

д

д

к

к

к

К3,3

К5

Для

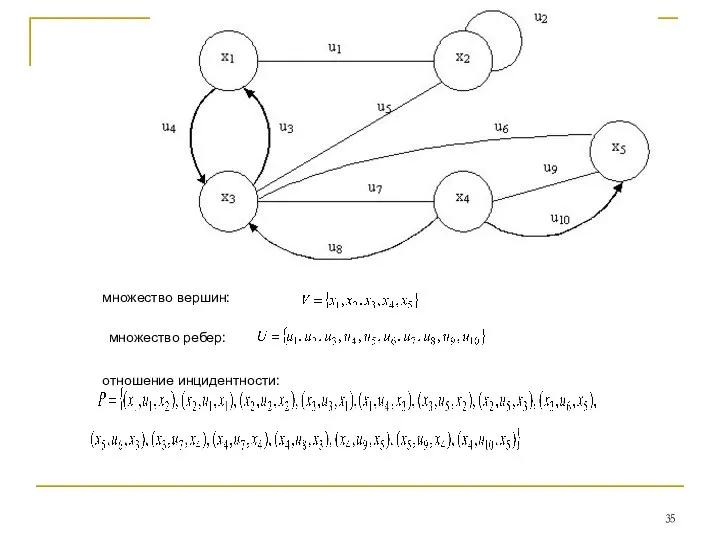
Способы задания графов

Явное задание графа в виде двух множеств вершин V

множество вершин:

множество ребер:

отношение инцидентности:

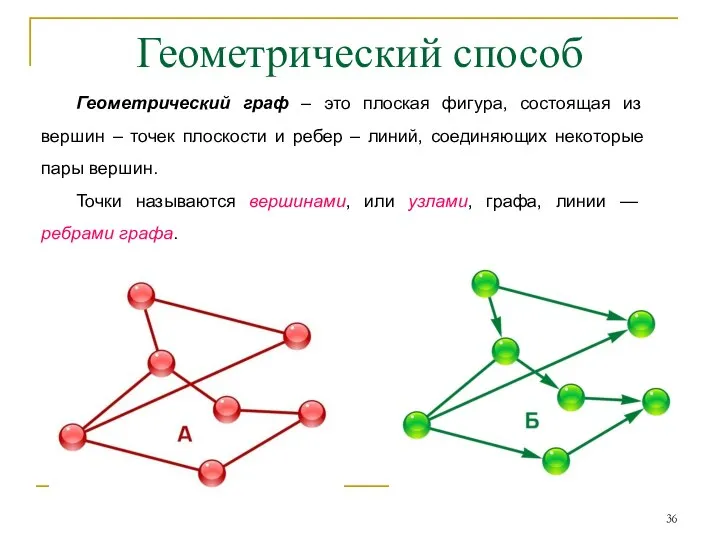
Геометрический способ

Геометрический граф – это плоская фигура, состоящая из вершин –

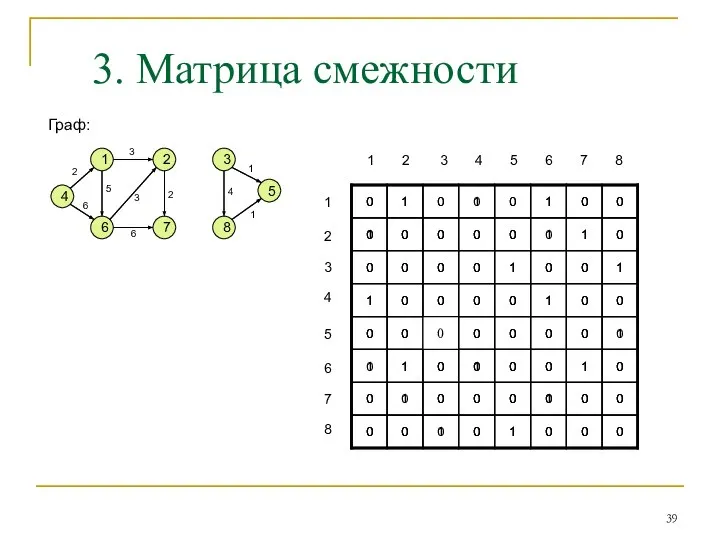
3. Матрица смежности

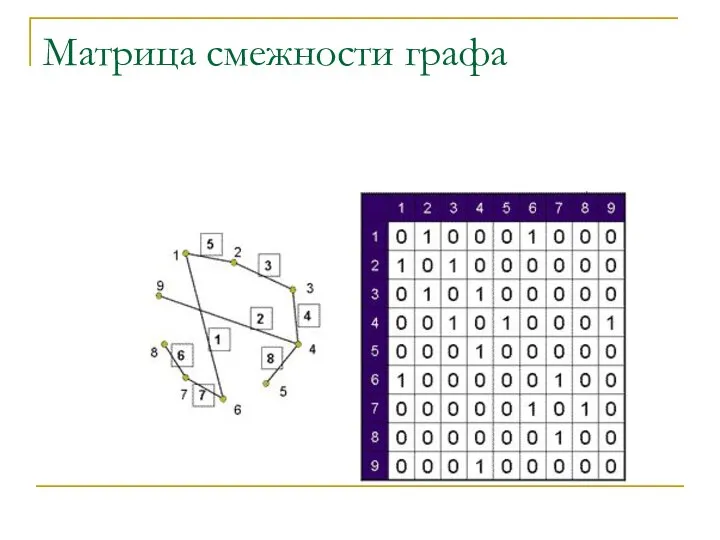
Матрица смежности графа

Граф:

4

1

6

7

2

3

8

5

1 2 3 4 5 6 7 8

1

2

3

4

5

6

7

8

3

5

3

1

4

2

6

2

6

1

3. Матрица смежности

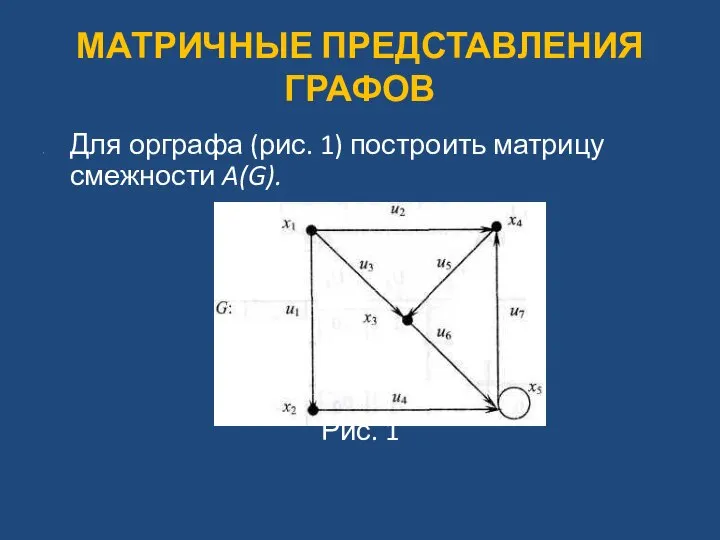
МАТРИЧНЫЕ ПРЕДСТАВЛЕНИЯ ГРАФОВ

Для орграфа (рис. 1) построить матрицу смежности A(G).
Рис. 1

МАТРИЧНЫЕ ПРЕДСТАВЛЕНИЯ ГРАФОВ

4. Матрица инцидентности

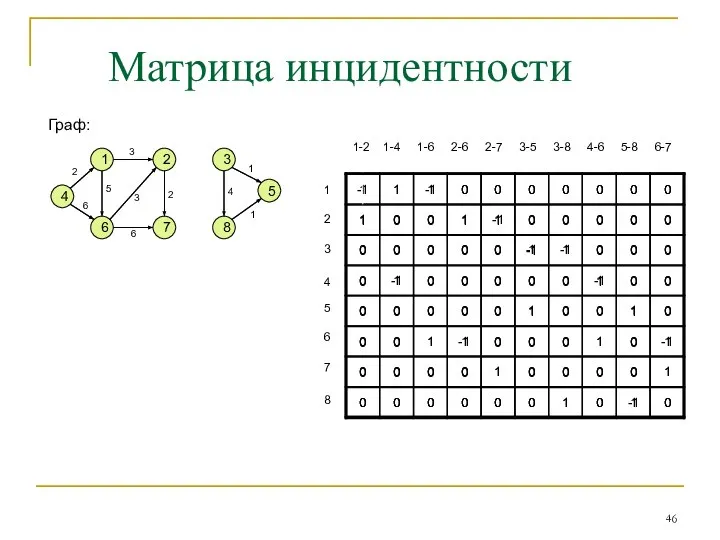
МАТРИЧНЫЕ ПРЕДСТАВЛЕНИЯ ГРАФОВ

Матрицей инциденций B(G) = {bik] орграфа
G = (X,U)

МАТРИЧНЫЕ ПРЕДСТАВЛЕНИЯ ГРАФОВ

В матрице инциденций для неографа при ее построении элементы

Граф:

4

1

6

7

2

3

8

5

3

5

3

1

4

2

6

2

6

1

1-2 1-4 1-6 2-6 2-7 3-5 3-8 4-6 5-8 6-7

1

2

3

4

5

6

7

8

Матрица инцидентности

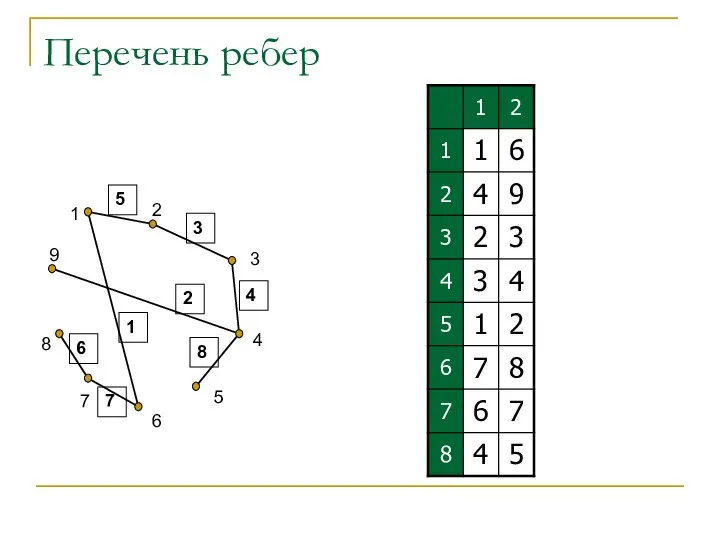
Перечень (списки) ребер

Для хранения перечня ребер необходим двумерный массив размерности M×2.
Строка

Перечень ребер

1

2

3

4

5

6

7

8

9

1

2

3

4

5

6

7

8

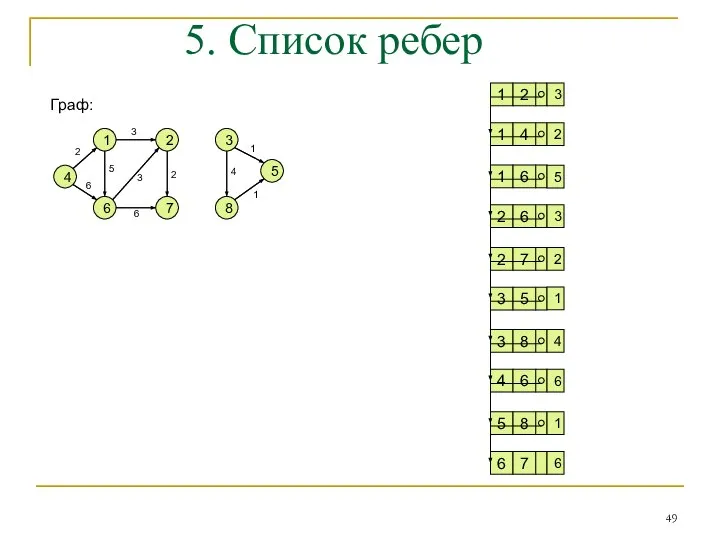
4

1

6

7

2

3

8

5

3

5

3

1

4

2

6

2

6

1

Граф:

1

2

1

4

1

6

2

6

2

7

3

5

3

8

4

6

5

8

6

7

3

2

5

3

2

1

4

6

1

6

5. Список ребер

Пути и маршруты

1

2

3

4

5

6

7

8

1 – 2 – 3 – 7

– 8 –

Расстоянием между двумя вершинами называется минимальная длина из всех возможных маршрутов

В орграфе маршрут является ориентированным и называется путем. На путь сразу

Длина пути – это количество ребер в нем.
Путь называется простым, если

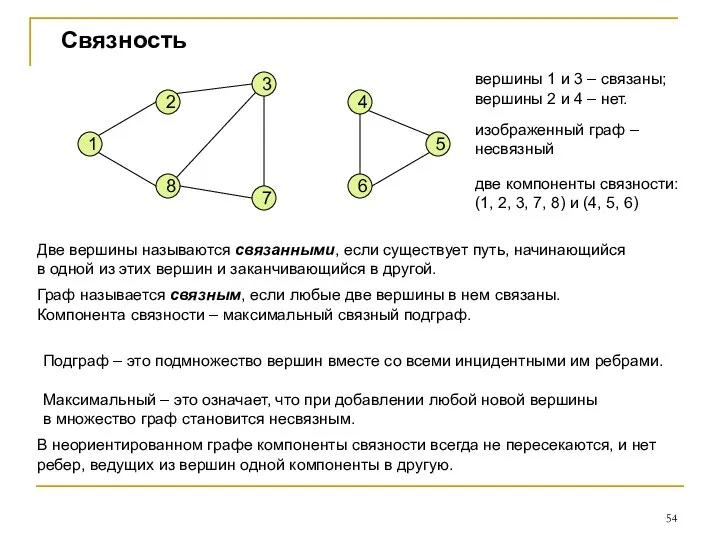
Связность

Две вершины называются связанными, если существует путь, начинающийся
в одной из этих

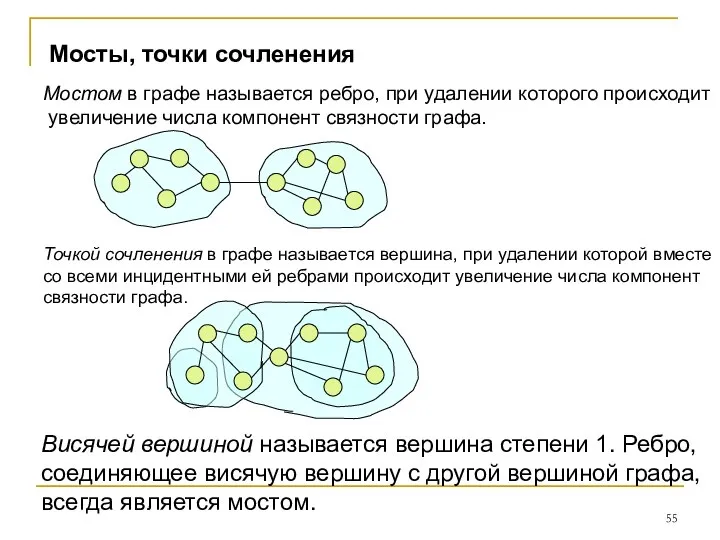
Мосты, точки сочленения

Мостом в графе называется ребро, при удалении которого происходит

Эйлеровы и гамильтоновы графы

Задача Эйлера (о кенигсбергских мостах)

Задача о семи кенигсбергских мостах.

Как пройти по

Эйлеровым путем в графе называется путь, содержащий все ребра графа. Эйлеровым

ЦИКЛЫ Эйлера

Эйлеров цикл содержит не только все ребра (по одному разу)

Теорема Эйлера о графах

Теорема (Эйлер). В связном неориентированном графе эйлеров путь

Теорема Эйлера об ориентированных графах

Алгоритм Флёри построения эйлерова цикла

Теорема. Пусть G – эйлеров граф;

Гамильтоновым путём (циклом) графа G называется путь (цикл), проходящий через каждую

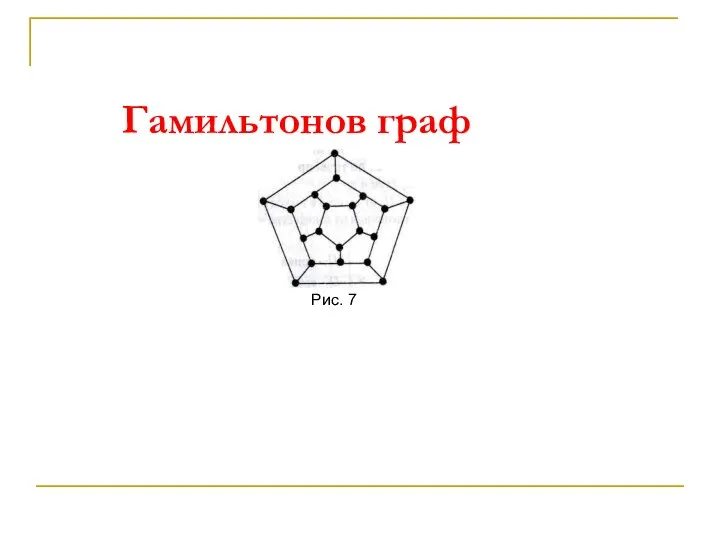
Гамильтонов граф
Рис. 7

Достаточны условия Гамильтонова графа

ЦИКЛЫ Эйлера и Гамильтона

Составляя задачи отыскания эйлеровых и гамильтоновых циклов, следует

Граф G называется планарным (плоским), если существует изоморфный ему граф ,

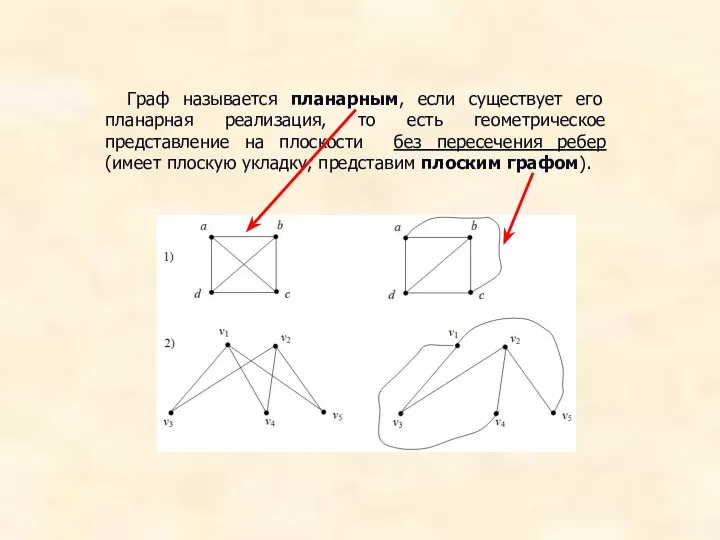
Граф называется планарным, если существует его планарная реализация, то есть геометрическое

ПРИМЕР соответствия плоского графа кубу

Непересекающиеся части плоскости, заключённые между циклами, образованными ребрами планарного графа, называются

Пример.
Данный граф выделяет
в плоскости следующие
области: А1 с границей q;
А2 с границей

Теорема (Эйлера) Если G – связный планарный граф, содержащий n вершин,