Содержание
- 2. Основы теории логических преобразований Математическая логика Логические операции и элементы Преобразование логических выражений
- 3. 1) Логика оказала влияние на развитие математики, прежде всего теории множеств, функциональных систем, алгоритмов, рекурсивных функций.
- 4. АЛГЕБРА ЛОГИКИ (ВЫСКАЗЫВАНИЙ) - РАЗДЕЛ МАТЕМАТИЧЕСКОЙ ЛОГИКИ, ИЗУЧАЮЩИЙ ВЫСКАЗЫВАНИЯ И ЛОГИЧЕСКИЕ ОПЕРАЦИИ НАД НИМИ.
- 5. Основные понятия Высказывание Простое и сложное высказывание
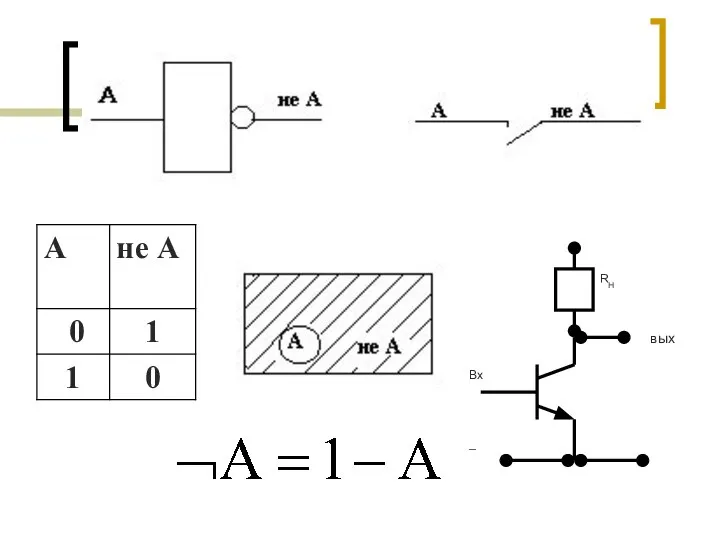
- 6. ИНВЕРСИЯ (ЛОГИЧЕСКОЕ ОТРИЦАНИЕ) - ПРИСОЕДИНЕНИЕ ЧАСТИЦЫ «НЕ» К СКАЗУЕМОМУ ДАННОГО ПРОСТОГО ВЫСКАЗЫВАНИЯ ИЛИ ПРИСОЕДИНЕНИЕ СЛОВ «НЕВЕРНО
- 7. 0 вых
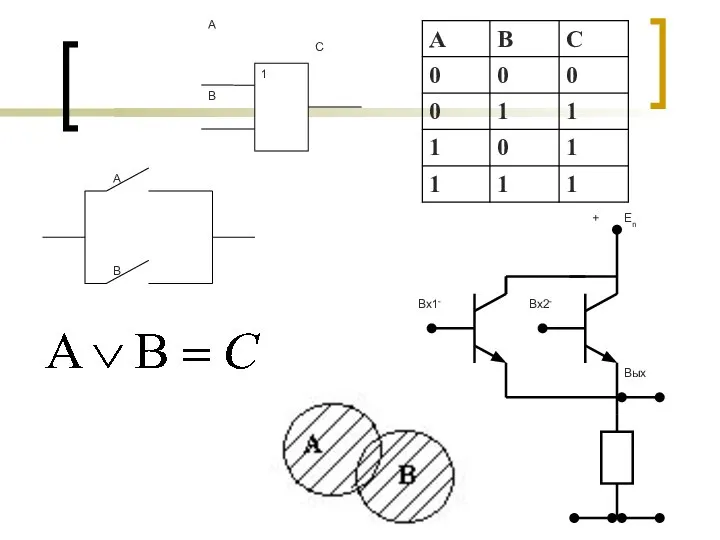
- 8. ДИЗЪЮНКЦИЯ (ЛОГИЧЕСКОЕ СЛОЖЕНИЕ) - СОЕДИНЕНИЕ ДВУХ ВЫСКАЗЫВАНИЙ А И В В ОДНО С ПОМОЩЬЮ СОЮЗА «ИЛИ»,
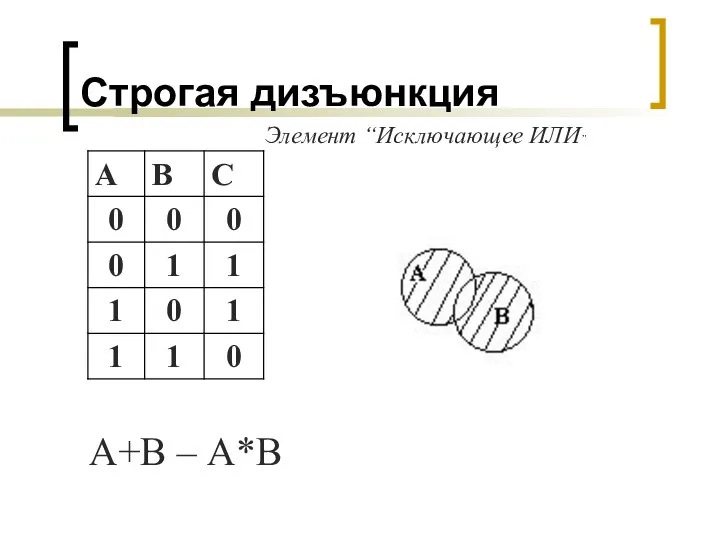
- 10. Строгая дизъюнкция А+В – А*В Элемент “Исключающее ИЛИ”
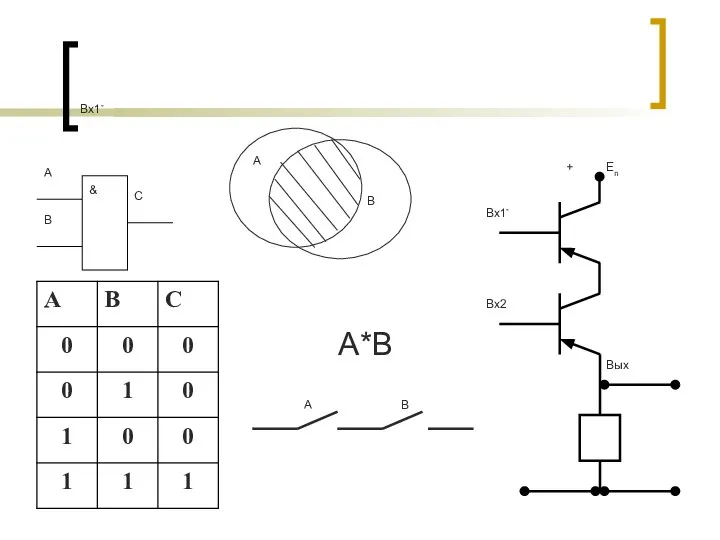
- 11. КОНЪЮНКЦИЯ (ЛОГИЧЕСКОЕ УМНОЖЕНИЕ) - СОЕДИНЕНИЕ ДВУХ ВЫСКАЗЫВАНИЙ А И В В ОДНО С ПОМОЩЬЮ СОЮЗА «И».
- 12. Вх1- А*В
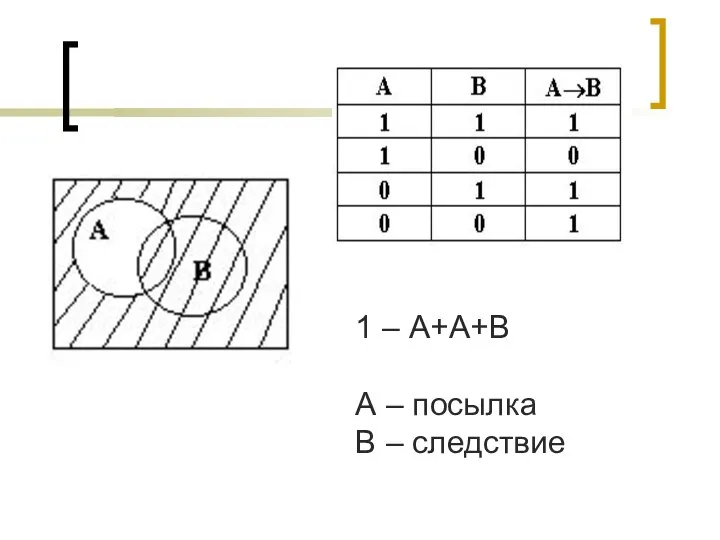
- 13. ИМПЛИКАЦИЯ - ЛОГИЧЕСКАЯ ОПЕРАЦИЯ, СООТВЕТСТВУЮЩАЯ СОЮЗУ «ЕСЛИ . . . , ТО . . .» ИМПЛИКАЦИЯ
- 14. 1 – А+А+В А – посылка В – следствие
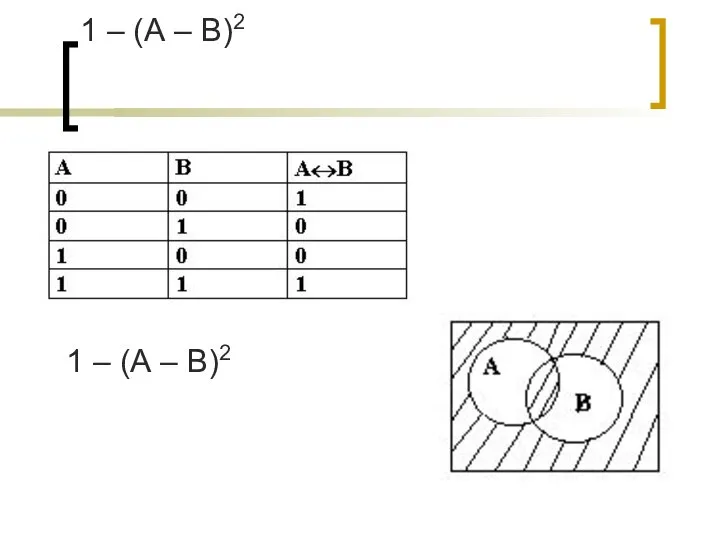
- 15. ЭКВИВАЛЕНЦИЯ - ЛОГИЧЕСКАЯ ОПЕРАЦИЯ, СООТВЕТСТВУЮЩАЯ СОЮЗУ «ТОГДА И ТОЛЬКО ТОГДА, КОГДА …» ЭКВИВАЛЕНЦИЯ ДВУХ ВЫСКАЗЫВАНИЙ ИСТИННА
- 16. 1 – (А – В)2 1 – (А – В)2
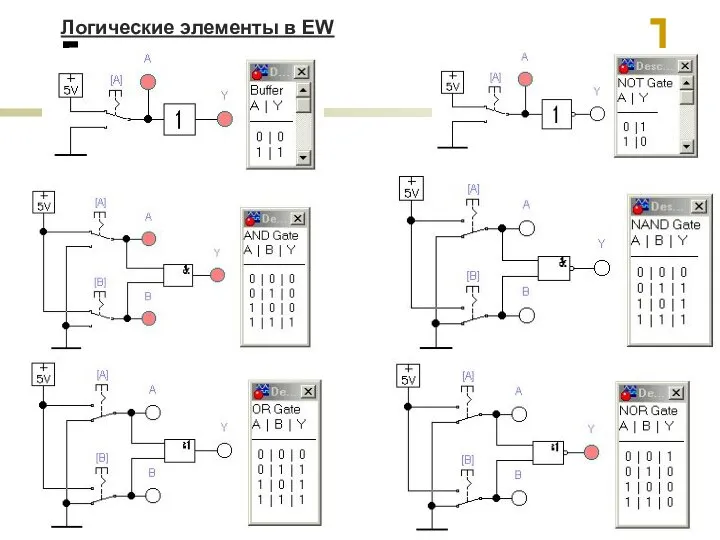
- 17. Логические элементы в EW
- 18. Логические функции Логической (булевой) функцией называют функцию Y=f(Х1, Х2 ..., Хn), аргументы которой Х1, Х2 ...,
- 19. СНДФ и СКНФ Если логическая функция представлена дизъюнкцией, конъюнкцией и инверсией, то такая форма представления называется
- 20. Совершенная дизъюнктивная нормальная форма (СДНФ)отвечает следующим требованиям: 1) в ней нет двух одинаковых элементарных конъюнкций; 2)
- 22. Алгоритм образования СДНФ по таблице истинности. 1. Выделить в таблице истинности все наборы переменных, на которых
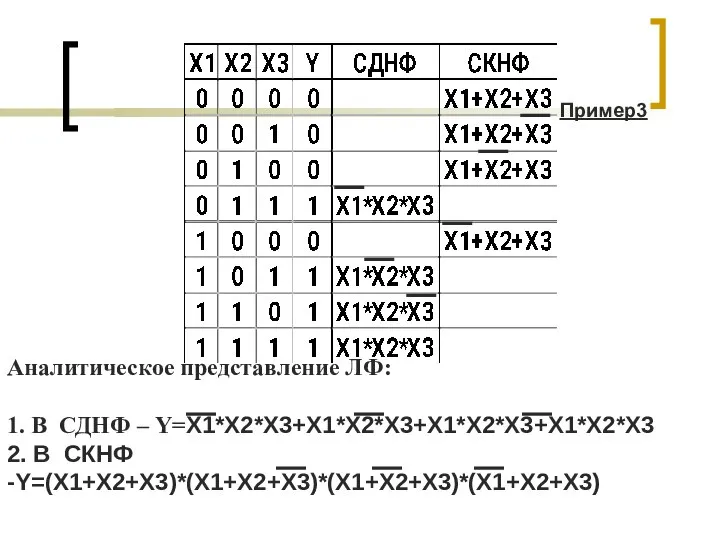
- 24. Аналитическое представление ЛФ: 1. В СДНФ – Y=X1*X2*X3+X1*X2*X3+X1*X2*X3+X1*X2*X3 2. В СКНФ -Y=(X1+X2+X3)*(X1+X2+X3)*(X1+X2+X3)*(X1+X2+X3) Пример3
- 25. Минимизация логических функций Цель минимизации ЛФ заключается уменьшение стоимости ее технической реализации при сохранении заданных характеристик.
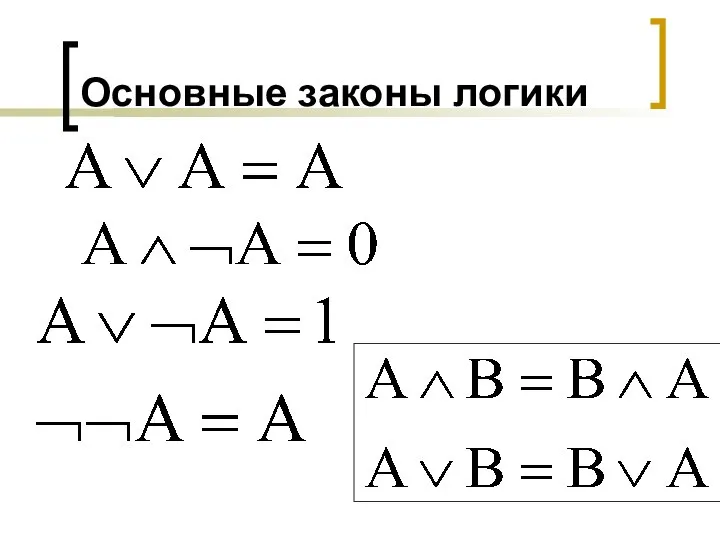
- 26. Основные законы логики
- 27. Основные законы логики
- 30. ВЫСКАЗЫВАНИЕ - ЭТО ПОВЕСТВОВАТЕЛЬНОЕ ПРЕДЛОЖЕНИЕ, О КОТОРОМ МОЖНО СКАЗАТЬ, ЧТО ОНО ИСТИННО ИЛИ ЛОЖНО. 1) Земля
- 31. ВЫСКАЗЫВАНИЕМ НЕ ЯВЛЯЕТСЯ: 1) ВОСКЛИЦАТЕЛЬНЫЕ И ВОПРОСИТЕЛЬНЫЕ ПРЕДЛОЖЕНИЯ. 2) ОПРЕДЕЛЕНИЯ. 3) ПРЕДЛОЖЕНИЯ ТИПА: «ОН СЕРОГЛАЗ» «X2-4X+3=0»
- 33. Скачать презентацию

















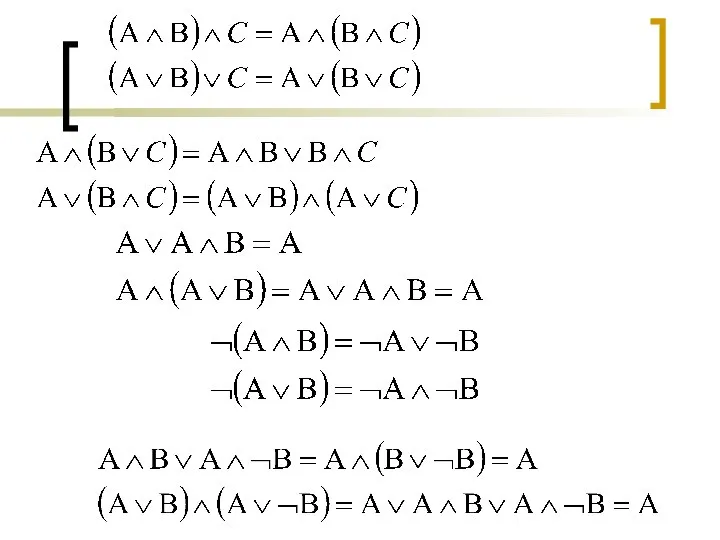



 Правило вычисления значения алгебраической суммы двух чисел
Правило вычисления значения алгебраической суммы двух чисел Геодезические сети. Лекция №4
Геодезические сети. Лекция №4 Сидоренко Ольга группа «СО-11»
Сидоренко Ольга группа «СО-11»  Площади (тест) 8 класс
Площади (тест) 8 класс Презентация по математике "Арифметические действия над натуральными числами" - скачать бесплатно
Презентация по математике "Арифметические действия над натуральными числами" - скачать бесплатно Множества и операции над ними
Множества и операции над ними Квадратичная функция. Парабола
Квадратичная функция. Парабола Вычитание (Помоги Буратино исправить ошибки)
Вычитание (Помоги Буратино исправить ошибки) Презентация на тему Построение диаграмм и графиков функций
Презентация на тему Построение диаграмм и графиков функций  Модуль числа. 6 класс
Модуль числа. 6 класс Ознайомлення з дробами
Ознайомлення з дробами Презентация на тему Действия с десятичными дробями
Презентация на тему Действия с десятичными дробями  Урок математики в 6 классе тема «Проценты. Решение задач». МОУ «Павлиновская средняя общеобразовательная школа» Учитель А
Урок математики в 6 классе тема «Проценты. Решение задач». МОУ «Павлиновская средняя общеобразовательная школа» Учитель А Показательные уравнения Эта тема не так сложна, как кажется, стоит лишь по-хорошему разобраться в ней, в чем я постараюсь помочь
Показательные уравнения Эта тема не так сложна, как кажется, стоит лишь по-хорошему разобраться в ней, в чем я постараюсь помочь Математическая сказка. Путешествие в сказку "Царевна-лягушка"
Математическая сказка. Путешествие в сказку "Царевна-лягушка" Решение примеров. Прибавление чисел к числу 10
Решение примеров. Прибавление чисел к числу 10 Теория матричных игр
Теория матричных игр Многогранники
Многогранники Пирамида
Пирамида Статистическое изучение динамики социально-правовых явлений и процессов
Статистическое изучение динамики социально-правовых явлений и процессов Басқару жүйесінің тұрақтылығы
Басқару жүйесінің тұрақтылығы Презентация по математике "Новогодняя телепрограмма" - скачать
Презентация по математике "Новогодняя телепрограмма" - скачать  Алгебра логики
Алгебра логики Дом дружбы народов. II региональный турнир по ментальной арифметике. Ижевск 2018
Дом дружбы народов. II региональный турнир по ментальной арифметике. Ижевск 2018 Презентация урока математики в 5 классе по теме: «Действия с десятичными дробями» С. Бабынино МКОУ «СОШ№1» Нагаевой А.Н.
Презентация урока математики в 5 классе по теме: «Действия с десятичными дробями» С. Бабынино МКОУ «СОШ№1» Нагаевой А.Н.  Основные методы решения тригонометрических уравнений
Основные методы решения тригонометрических уравнений Использование электронных образовательных ресурсов на уроках математики и информатики и физики
Использование электронных образовательных ресурсов на уроках математики и информатики и физики Числовые промежутки
Числовые промежутки