Содержание
- 2. Исследование остаточных величин. В задачу регрессионного анализа входит не только построение самой модели, но и исследование
- 3. Оценки параметров регрессии должны отвечать определенным критериям: Несмещенность оценки (математическое ожидание остатков равно нулю). Эффективность (оценки
- 4. Указанные критерии оценок (несмещенность, состоятельность, эффективность) обязательно учитываются при разных способах оценивания. Так как метод наименьших
- 5. Исследование остатков εi предполагают проверку наличия следующих пяти предпосылок МНК (теорема Гаусса-Маркова): случайный характер остатков; нулевая
- 6. Если распределение случайных остатков не соответствует некоторым предпосылкам МНК, то следует корректировать модель.
- 7. Прежде всего, проверяется случайный характер остатков - первая предпосылка МНК. С этой целью строится график зависимости
- 8. εi yi ∧
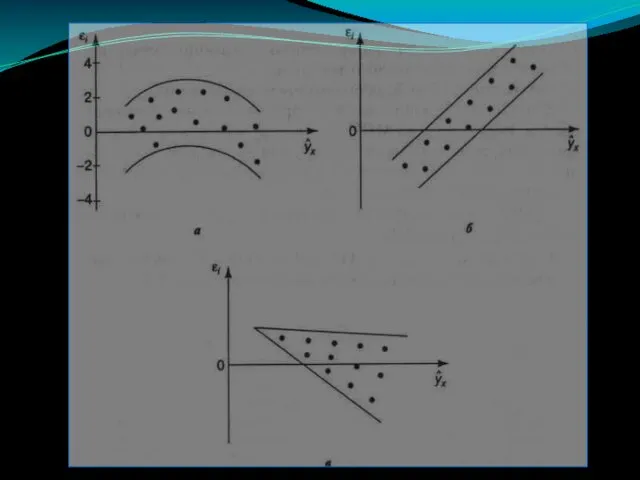
- 9. Если на графике получена горизонтальная полоса (из точек, как показано на рис.), то остатки εi представляют
- 11. В этих случаях необходимо либо применять другую функцию, либо вводить дополнительную информацию и заново строить уравнение
- 12. Вторая предпосылка МНК относительно нулевой средней величины остатков означает, что Это означает, что случайное отклонение в
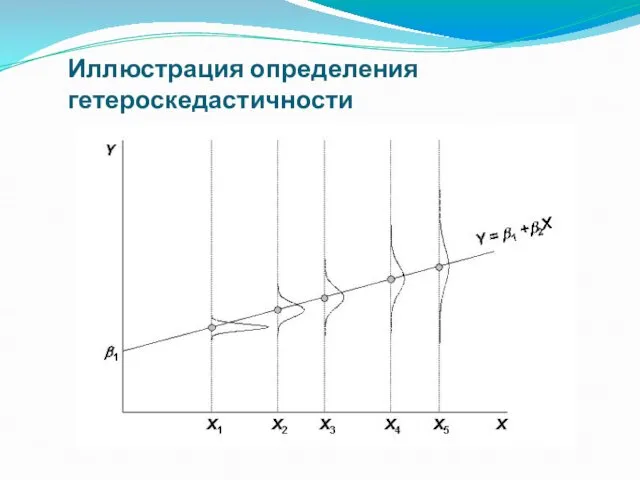
- 13. В соответствии с третьей предпосылкой МНК требуется, чтобы дисперсия остатков была гомоскедастичной. Это значит, что для
- 14. Иллюстрация определения гетероскедастичности
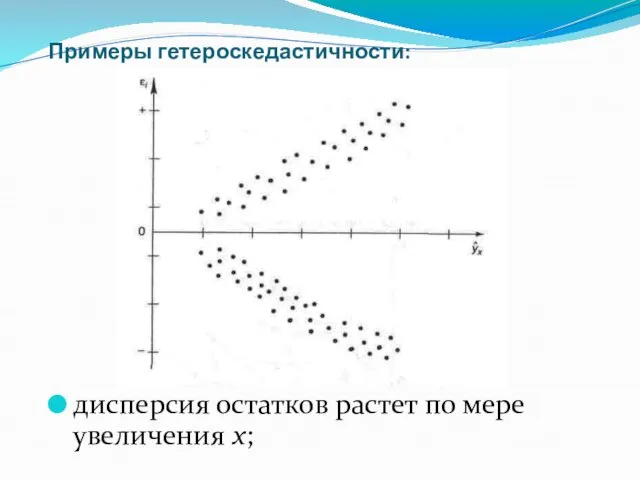
- 15. Примеры гетероскедастичности: дисперсия остатков растет по мере увеличения x;
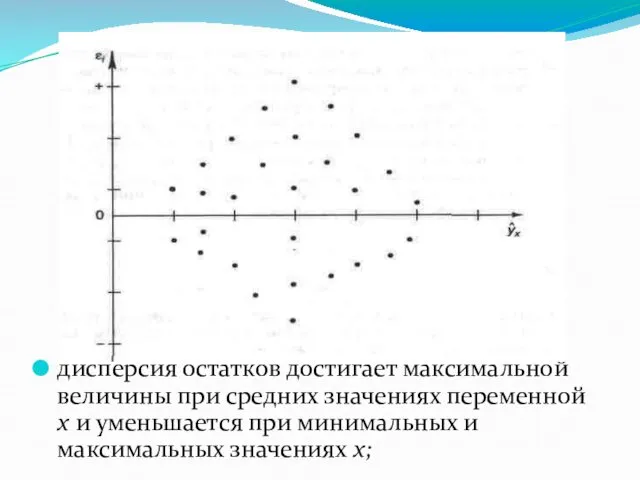
- 16. дисперсия остатков достигает максимальной величины при средних значениях переменной х и уменьшается при минимальных и максимальных
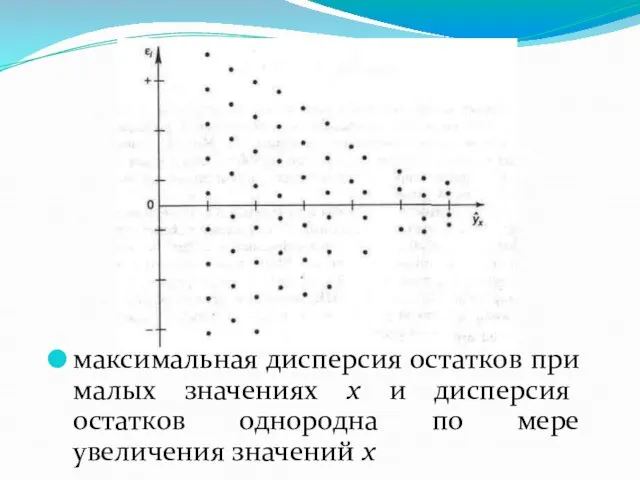
- 17. максимальная дисперсия остатков при малых значениях х и дисперсия остатков однородна по мере увеличения значений х
- 18. Метод Гольдфельда — Квандта При малом объеме выборки, что наиболее характерно для эконометрических исследований, для оценки
- 19. Упорядочение n наблюдений по мере возрастания переменной у. Исключение из рассмотрения С центральных наблюдений; при этом
- 20. Разделение совокупности из (n – C) наблюдений на две группы (соответственно с малыми и большими значениями
- 21. При выполнении нулевой гипотезы о гомоскедастичности отношение R будет удовлетворять F -критерию с (n-C-2p):2 степенями свободы
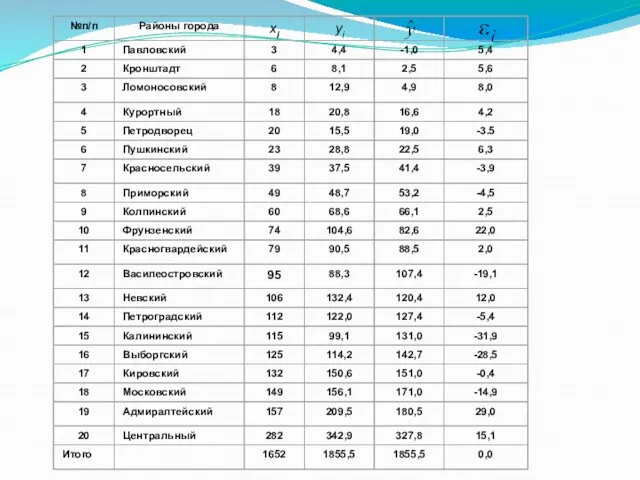
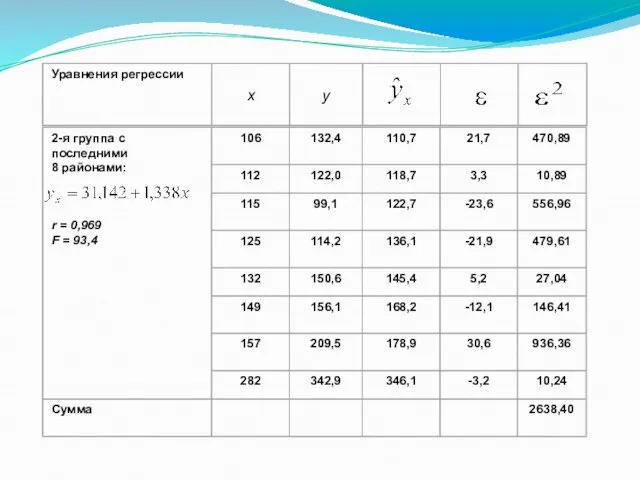
- 22. Пример использования метода Гольдфельда — Квандта Поступление доходов в бюджет Санкт-Петербурга (у — млрд руб.) в
- 24. В соответствии с уравнением найдены теоретические значения и отклонения от их фактических значений , т. е.
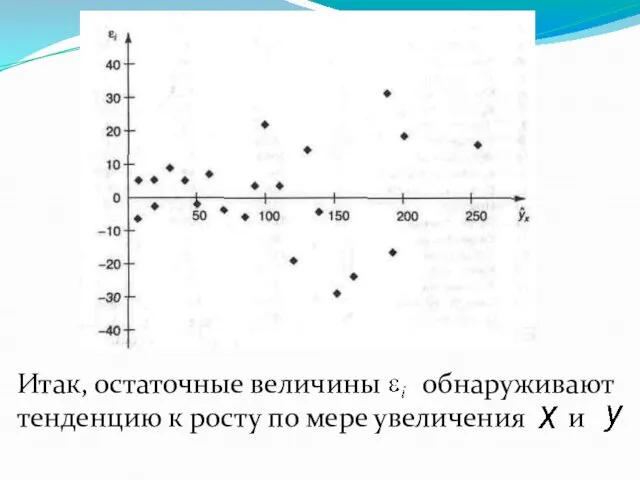
- 25. Итак, остаточные величины обнаруживают тенденцию к росту по мере увеличения и
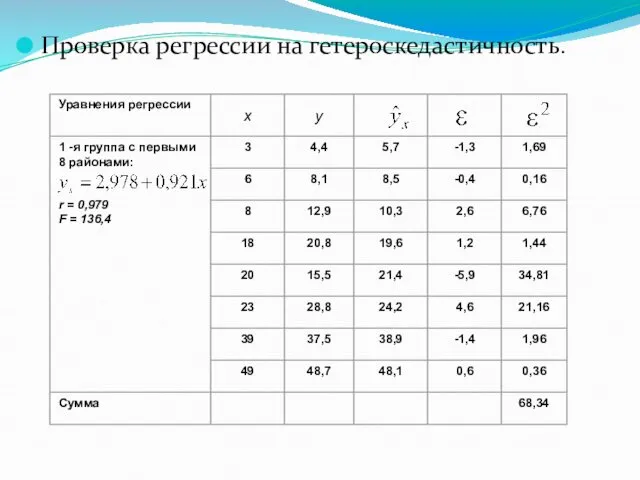
- 26. Этот вывод подтверждается и по критерию Гольдфельда – Квандта. Для его применения необходимо определить сначала число
- 27. Проверка регрессии на гетероскедастичность.
- 29. Величина , что превышает табличное значение – F-критерия 4,28 при 5 %-ном уровне значимости для числа
- 30. Четвертая предпосылка МНК - отсутствие автокорреляции остатков, т. е. значения остатков распределены независимо друг от друга.
- 31. Автокорреляция остатков означает наличие корреляции между остатками текущих и предыдущих (последующих) наблюдений. Коэффициент корреляции между и
- 32. При использовании F-критерия Фишера и t-критерия Стьюдента делаются предположения относительно поведения остатков –остатки представляют собой независимые
- 33. Наряду с предпосылками МНК должны соблюдаться определенные требования относительно переменных, включаемых в модель: соотношение 1 фактор
- 34. Обобщенный метод наименьших квадратов
- 35. Обобщенный метод наименьших квадратов При нарушении гомоскедастичности и наличии автокорреляции остатков рекомендуется вместо традиционного МНК использовать
- 36. Метод взвешенных наименьших квадратов. Случай парной регрессии Получили уравнение регрессии без свободного члена, но с дополнительной
- 37. Метод взвешенных наименьших квадратов. Случай парной регрессии На практике, значения дисперсии остатков, как правило, не известны.
- 39. Скачать презентацию



























 Методика изучения двумерных геометрических фигур: виды углов; ломаная, многоугольники и их виды; прямоугольник, квадрат
Методика изучения двумерных геометрических фигур: виды углов; ломаная, многоугольники и их виды; прямоугольник, квадрат Презентация на тему Рациональные формы вычислений
Презентация на тему Рациональные формы вычислений  Пропорциональные отрезки в прямоугольном треугольнике
Пропорциональные отрезки в прямоугольном треугольнике Презентация по математике "Функция арифметического квадратного корня, её свойства" - скачать бесплатно
Презентация по математике "Функция арифметического квадратного корня, её свойства" - скачать бесплатно Золотое сечение
Золотое сечение Боковая сторона равнобедренной трапеции
Боковая сторона равнобедренной трапеции Системы уравнений и их графическое решение
Системы уравнений и их графическое решение Занимательная математика
Занимательная математика Моделирование как метод научного познания. Общие свойства моделей
Моделирование как метод научного познания. Общие свойства моделей Математика. Что такое периметр?
Математика. Что такое периметр? Параллельное проектирование и его свойства. (10 класс)
Параллельное проектирование и его свойства. (10 класс) Определение подобных треугольников
Определение подобных треугольников Выполнил: Ученик 10 кл Сивожелезов Михаил МОУ СОШ № 7 г.Соль –Илецк Оренбургской обл
Выполнил: Ученик 10 кл Сивожелезов Михаил МОУ СОШ № 7 г.Соль –Илецк Оренбургской обл Тригонометрические уравнения
Тригонометрические уравнения Материал для внеклассной работы по математике. Бедный заяц (сказка)
Материал для внеклассной работы по математике. Бедный заяц (сказка) Методы и системы компьютерной математики. Преобразование Фурье и Лапласса в системе Mathematica,maple,mathcad
Методы и системы компьютерной математики. Преобразование Фурье и Лапласса в системе Mathematica,maple,mathcad Кафедра высшей математики
Кафедра высшей математики Тригонометрический круг
Тригонометрический круг Числа Фибоначчи
Числа Фибоначчи Площадь трапеции
Площадь трапеции Относительные показатели: динамики, плана, координации
Относительные показатели: динамики, плана, координации Прикладна статистика та ймовірнісні процеси
Прикладна статистика та ймовірнісні процеси Метричесие задачи поверхности. (Лекция 3)
Метричесие задачи поверхности. (Лекция 3) Вычисление значений функции по формуле
Вычисление значений функции по формуле Історія розвитку поняття "функція" (9 клас)
Історія розвитку поняття "функція" (9 клас) Функции. Определение функции
Функции. Определение функции Лекция 6. Методы численного интегрирования
Лекция 6. Методы численного интегрирования Определение.Модуль числа а.
Определение.Модуль числа а.