Содержание
- 2. Теория без практики мертва или бесплодна, практика без теории невозможна или пагубна. Для теории нужны знания,
- 3. Математическим выражением взаимной связи реальных величин является идея функциональной зависимости. Понятие функции – важнейшее понятие математики.
- 4. Исследование функции: D(f) E(f) промежутки возрастантия и убывания четность и т.п…
- 5. Четность, нечетность функций Периодичность Нули функции Промежутки знакопостоянства Монотонность функции Повторение далее
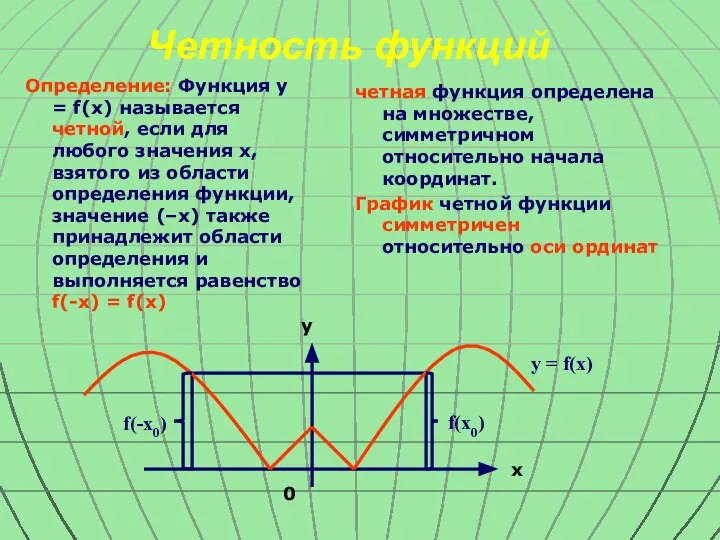
- 6. Четность функций Определение: Функция y = f(x) называется четной, если для любого значения x, взятого из
- 7. f(-x0) O y = f(x) Нечетность функций Определение: Функция y = f(x) называется нечетной, если для
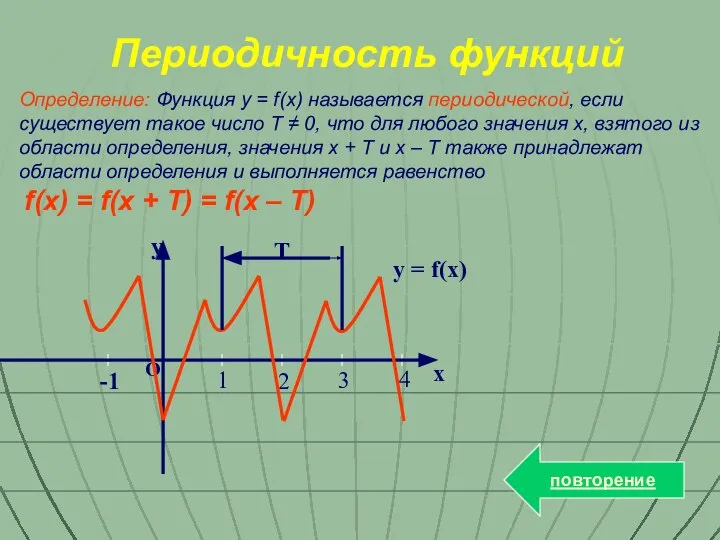
- 8. Определение: Функция y = f(x) называется периодической, если существует такое число T ≠ 0, что для
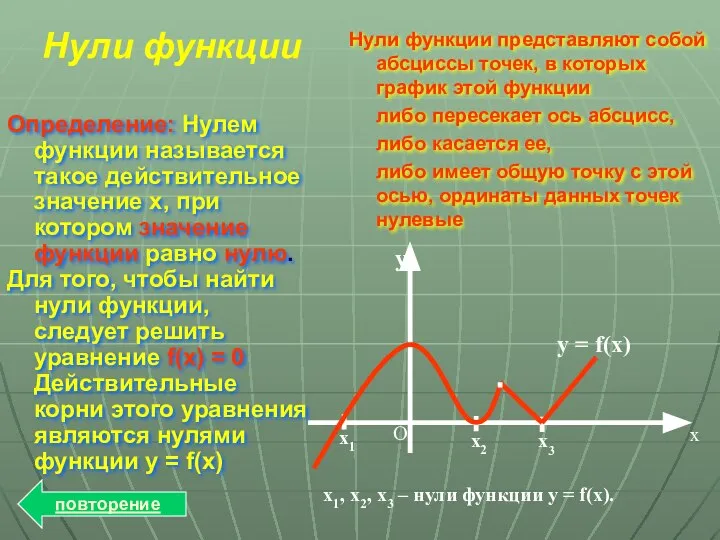
- 9. х1, х2, х3 – нули функции у = f(x). Нули функции Определение: Нулем функции называется такое
- 10. Промежутки знакопостоянства Определение: Числовые промежутки, на которых непрерывная функция сохраняет свой знак и не обращается в
- 11. Монотонность функции Определение: Функцию называют монотонно возрастающей, если с увеличением аргумента значение функции увеличивается, и монотонно
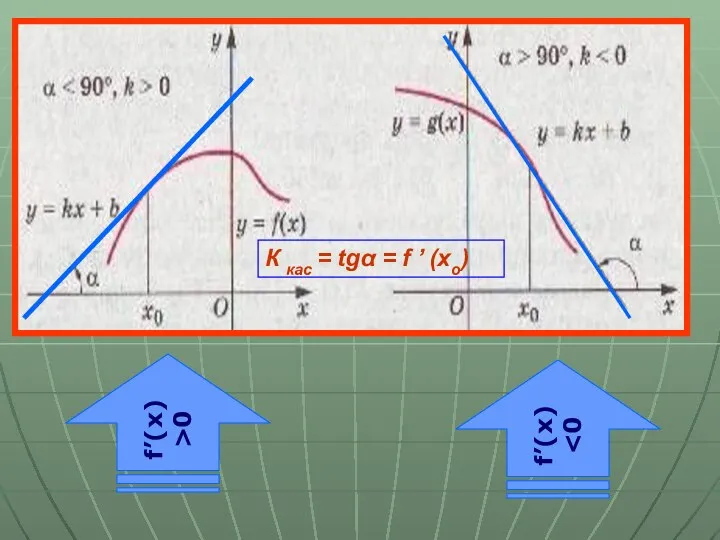
- 12. Если производная функции в каждой точке некоторого промежутка положительна, то функция на этом промежутке возрастает, т.е.f’(x)>0,
- 13. f’(x)>0 f’(x) К кас = tgα = f ’ (xo)
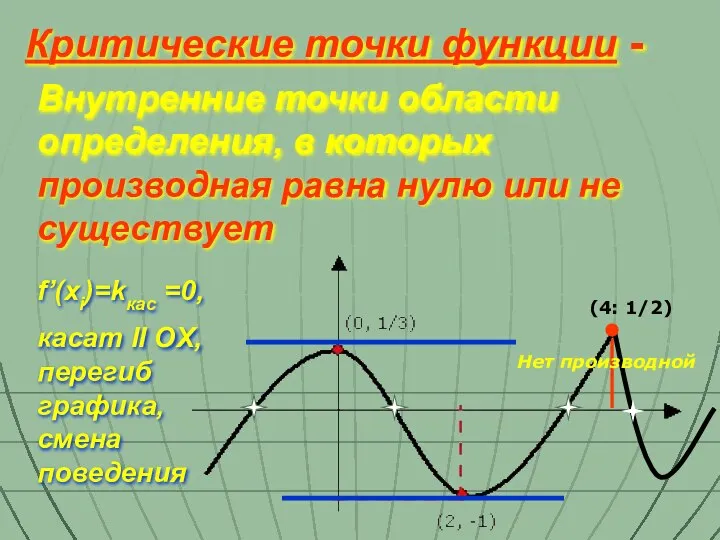
- 14. Внутренние точки области определения, в которых производная равна нулю или не существует Критические точки функции -
- 15. критические точки Достаточный признак возрастания или убывания функции Пример: Найти промежутки возрастания и убывания функции f(x)=х3
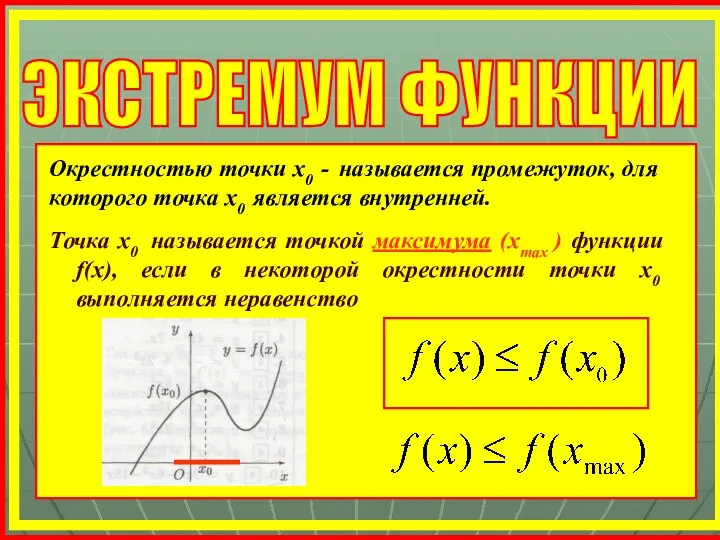
- 16. ЭКСТРЕМУМ ФУНКЦИИ Точка х0 называется точкой максимума (xmax ) функции f(x), если в некоторой окрестности точки
- 17. Точка х1 называется точкой минимума (xmin ) функции f(x), если в некоторой окрестности точки х1 выполняется
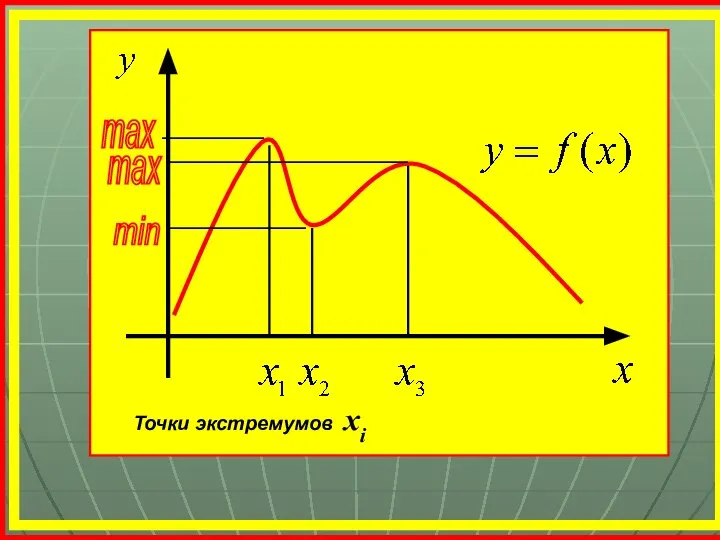
- 18. max min max Точки экстремумов хі
- 20. Скачать презентацию










 Методика изучения двумерных геометрических фигур: виды углов; ломаная, многоугольники и их виды; прямоугольник, квадрат
Методика изучения двумерных геометрических фигур: виды углов; ломаная, многоугольники и их виды; прямоугольник, квадрат Презентация на тему Рациональные формы вычислений
Презентация на тему Рациональные формы вычислений  Пропорциональные отрезки в прямоугольном треугольнике
Пропорциональные отрезки в прямоугольном треугольнике Презентация по математике "Функция арифметического квадратного корня, её свойства" - скачать бесплатно
Презентация по математике "Функция арифметического квадратного корня, её свойства" - скачать бесплатно Золотое сечение
Золотое сечение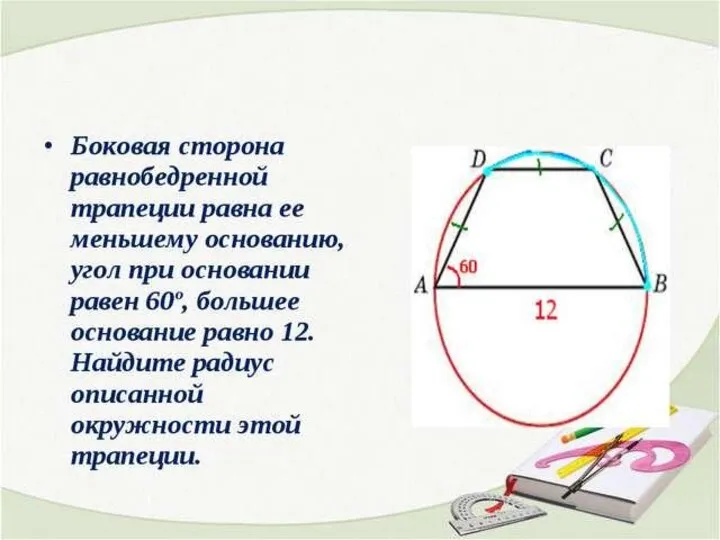 Боковая сторона равнобедренной трапеции
Боковая сторона равнобедренной трапеции Системы уравнений и их графическое решение
Системы уравнений и их графическое решение Занимательная математика
Занимательная математика Моделирование как метод научного познания. Общие свойства моделей
Моделирование как метод научного познания. Общие свойства моделей Математика. Что такое периметр?
Математика. Что такое периметр? Параллельное проектирование и его свойства. (10 класс)
Параллельное проектирование и его свойства. (10 класс) Определение подобных треугольников
Определение подобных треугольников Выполнил: Ученик 10 кл Сивожелезов Михаил МОУ СОШ № 7 г.Соль –Илецк Оренбургской обл
Выполнил: Ученик 10 кл Сивожелезов Михаил МОУ СОШ № 7 г.Соль –Илецк Оренбургской обл Тригонометрические уравнения
Тригонометрические уравнения Материал для внеклассной работы по математике. Бедный заяц (сказка)
Материал для внеклассной работы по математике. Бедный заяц (сказка) Методы и системы компьютерной математики. Преобразование Фурье и Лапласса в системе Mathematica,maple,mathcad
Методы и системы компьютерной математики. Преобразование Фурье и Лапласса в системе Mathematica,maple,mathcad Кафедра высшей математики
Кафедра высшей математики Тригонометрический круг
Тригонометрический круг Числа Фибоначчи
Числа Фибоначчи Площадь трапеции
Площадь трапеции Относительные показатели: динамики, плана, координации
Относительные показатели: динамики, плана, координации Прикладна статистика та ймовірнісні процеси
Прикладна статистика та ймовірнісні процеси Метричесие задачи поверхности. (Лекция 3)
Метричесие задачи поверхности. (Лекция 3) Вычисление значений функции по формуле
Вычисление значений функции по формуле Історія розвитку поняття "функція" (9 клас)
Історія розвитку поняття "функція" (9 клас) Функции. Определение функции
Функции. Определение функции Лекция 6. Методы численного интегрирования
Лекция 6. Методы численного интегрирования Определение.Модуль числа а.
Определение.Модуль числа а.