Содержание
- 2. Теоремы (theorems) алгебры переключений представляют собой заведомо верные утверждения, которые позволяют преобразовывать алгебраические выражения, чтобы упростить
- 3. Теоремы алгебры переключений для функций одной переменной (Т1) Х + 0 = Х (Tl') X •
- 4. Теоремы алгебры переключений для функций двух и трех переменных
- 5. Логические элементы (базовые) Логический элемент НЕ обозначается на схемах следующим образом: (пишется X c чертой сверху)
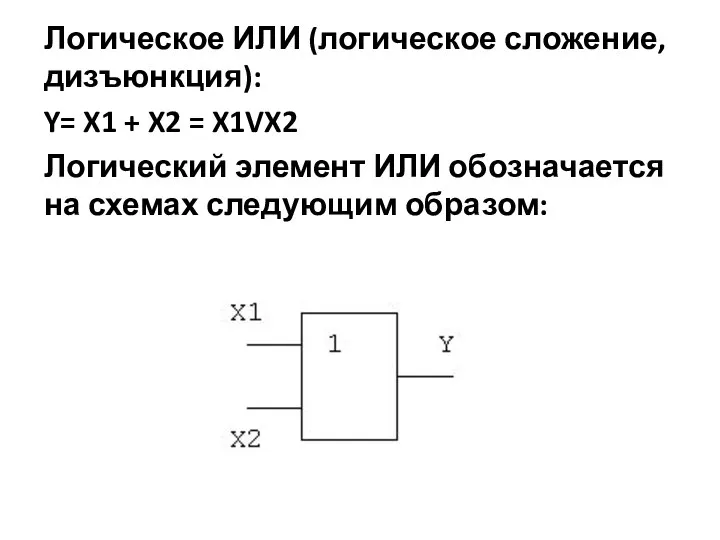
- 6. Логическое ИЛИ (логическое сложение, дизъюнкция): Y= X1 + X2 = X1VX2 Логический элемент ИЛИ обозначается на
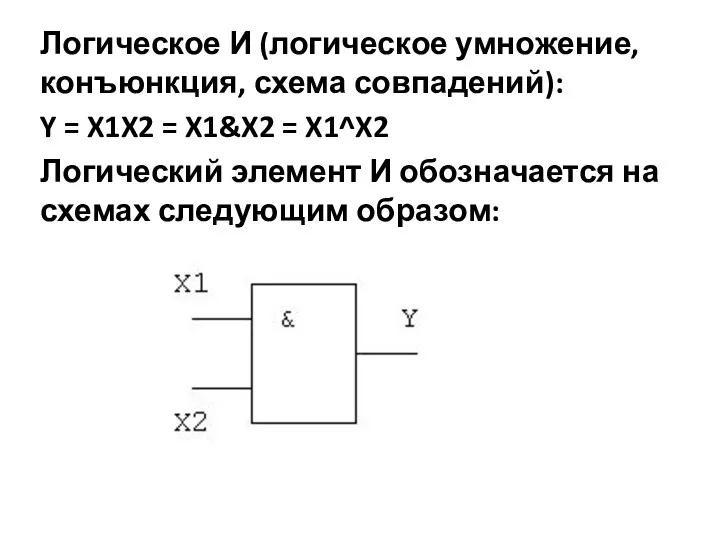
- 7. Логическое И (логическое умножение, конъюнкция, схема совпадений): Y = X1X2 = X1&X2 = X1^X2 Логический элемент
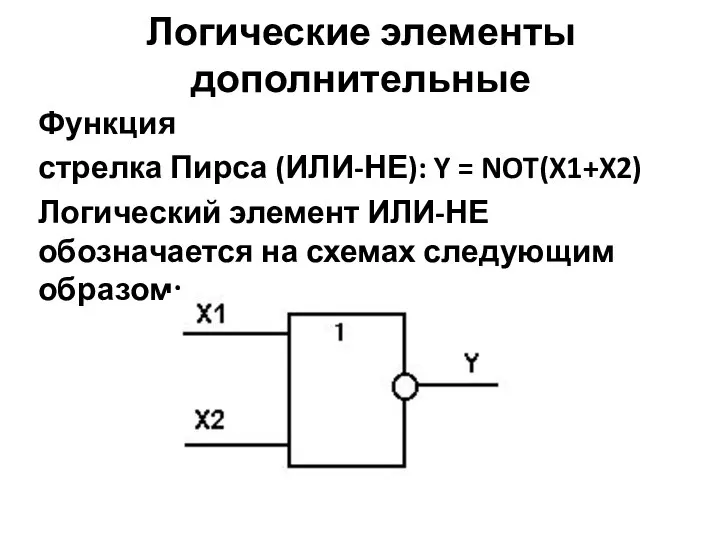
- 8. Функция стрелка Пирса (ИЛИ-НЕ): Y = NOT(X1+X2) Логический элемент ИЛИ-НЕ обозначается на схемах следующим образом: Логические
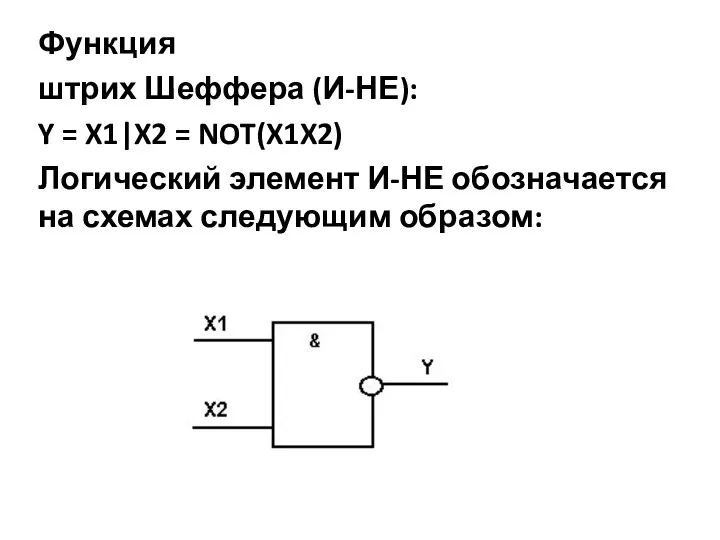
- 9. Функция штрих Шеффера (И-НЕ): Y = X1|X2 = NOT(X1X2) Логический элемент И-НЕ обозначается на схемах следующим
- 10. Найти сокращенную ДНФ для функции Применяя правило обобщенного склеивания правило поглощения и находим сокращенную ДНФ
- 11. Если в произвольной КНФ булевой функции раскрыть все скобки в соответствии с дистрибутивным законом и устранить
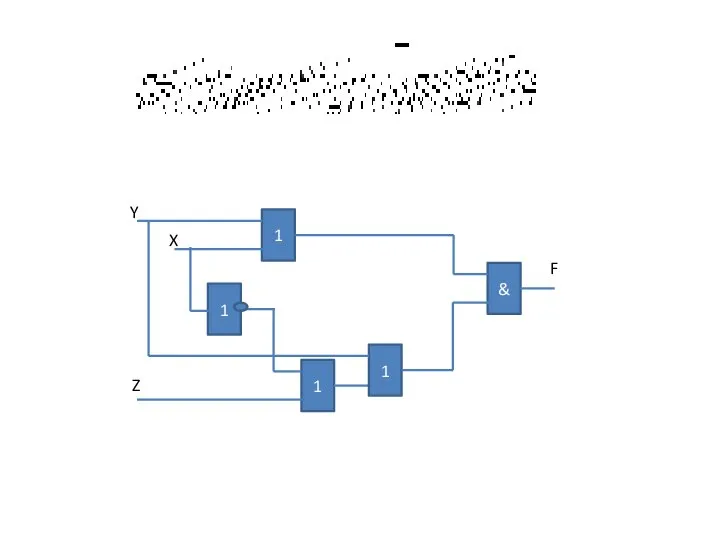
- 12. 1 1 1 & 1 Y X Z F
- 13. Построить схему реализации функций и сравнить результаты
- 16. Скачать презентацию








 Сложение и вычитание многочленов
Сложение и вычитание многочленов Перестановки. Лекция 23
Перестановки. Лекция 23 Счет до восьми. Число и цифра 8
Счет до восьми. Число и цифра 8 Систематические погрешности
Систематические погрешности Маршруты. Расстояния
Маршруты. Расстояния Повторение курса математики начальной школы
Повторение курса математики начальной школы Оптимізація об’єктів в статичних режимах. Метод множників лагранжа. (Лабораторна робота 1)
Оптимізація об’єктів в статичних режимах. Метод множників лагранжа. (Лабораторна робота 1) Правильные многогранники. Материалы к уроку геометрии в 10 классе
Правильные многогранники. Материалы к уроку геометрии в 10 классе Координатно-параметрический метод решения задач с параметрами
Координатно-параметрический метод решения задач с параметрами Взаимная перпендикулярность фигур. Задание многогранников на эпюре Монжа. (Лекция 7)
Взаимная перпендикулярность фигур. Задание многогранников на эпюре Монжа. (Лекция 7) Перпендикулярность прямой и плоскости
Перпендикулярность прямой и плоскости Обыкновенные дроби
Обыкновенные дроби Методы решения тригонометрических уравнений
Методы решения тригонометрических уравнений Окружность. Длина окружности
Окружность. Длина окружности Арифметическая прогрессия
Арифметическая прогрессия Свойство биссектрисы угла
Свойство биссектрисы угла Тренажер. Табличное умножение
Тренажер. Табличное умножение Аттестационная работа. Кружок «Юный математик»
Аттестационная работа. Кружок «Юный математик» Комплексные числа
Комплексные числа Решение задач по стереометрии
Решение задач по стереометрии Сложение и вычитание дробей с одинаковыми знаменателями
Сложение и вычитание дробей с одинаковыми знаменателями Кривые 2-го порядка
Кривые 2-го порядка Поиски различных способов решения планиметрической задачи УРОВЕНЬ С4 УЧИТЕЛЬ МАТЕМАТИКИ ГБОУ СОШ №1358 г. МОСКВЫ ЕПИФАНОВА Т
Поиски различных способов решения планиметрической задачи УРОВЕНЬ С4 УЧИТЕЛЬ МАТЕМАТИКИ ГБОУ СОШ №1358 г. МОСКВЫ ЕПИФАНОВА Т Презентация на тему Перевод чисел в десятичную систему счисления 11 класс
Презентация на тему Перевод чисел в десятичную систему счисления 11 класс Математика. Умножение трехзначных чисел. 3 класс
Математика. Умножение трехзначных чисел. 3 класс Практика по темам «Последовательность» и «Арифметическая прогрессия»
Практика по темам «Последовательность» и «Арифметическая прогрессия» Числовой луч (1 класс)
Числовой луч (1 класс) Презентация по математике Сложение и вычитание дробей с разными знаменателями.
Презентация по математике Сложение и вычитание дробей с разными знаменателями.