Содержание
- 2. Из истории математики В 1672 г. Датский математик Георг Мор, а затем в 1797 г. итальянский
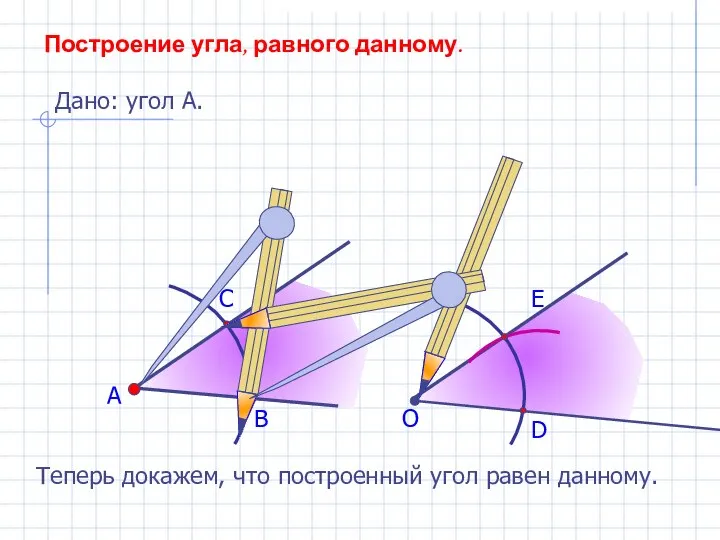
- 3. А В С Построение угла, равного данному. Дано: угол А. О D E Теперь докажем, что
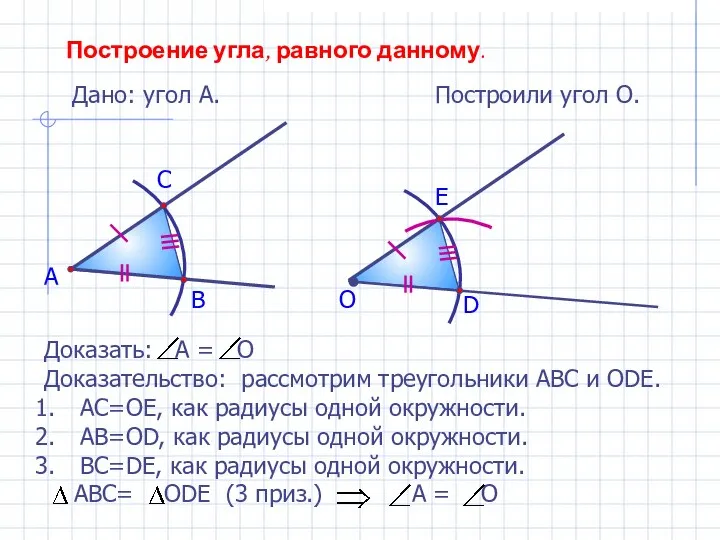
- 4. Построение угла, равного данному. Дано: угол А. А Построили угол О. В С О D E
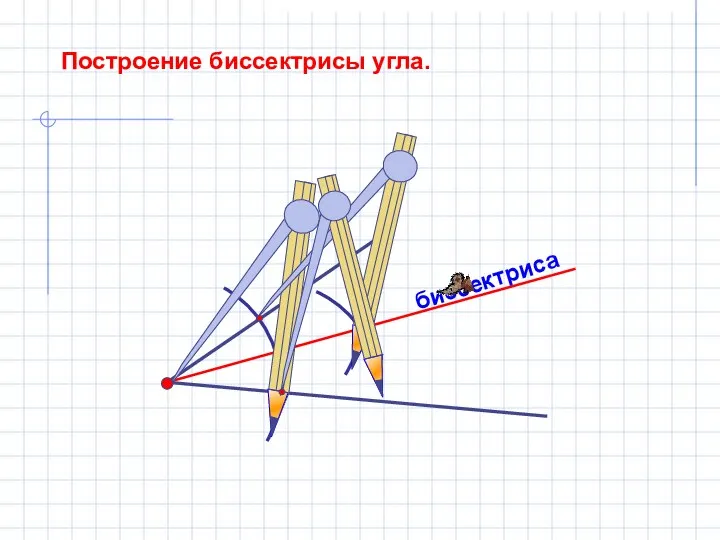
- 5. биссектриса Построение биссектрисы угла.
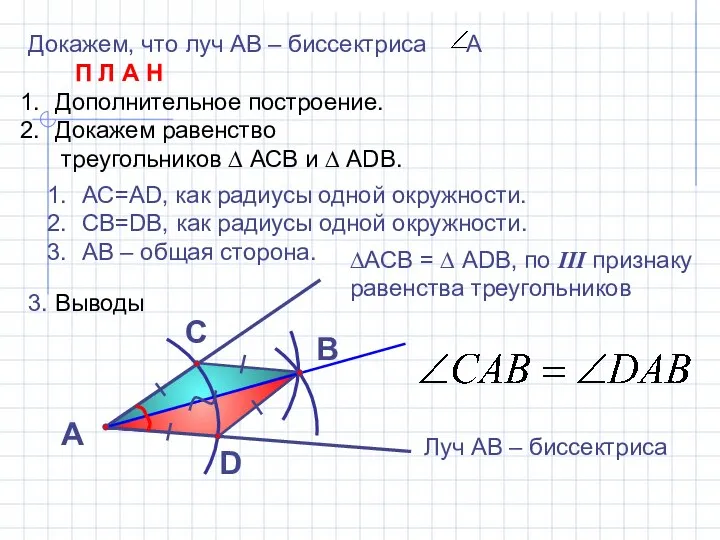
- 6. Докажем, что луч АВ – биссектриса А П Л А Н Дополнительное построение. Докажем равенство треугольников
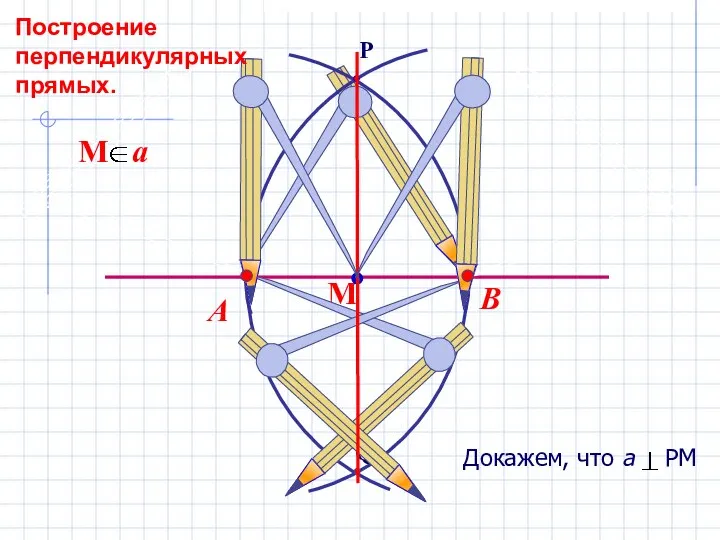
- 7. В А Построение перпендикулярных прямых.
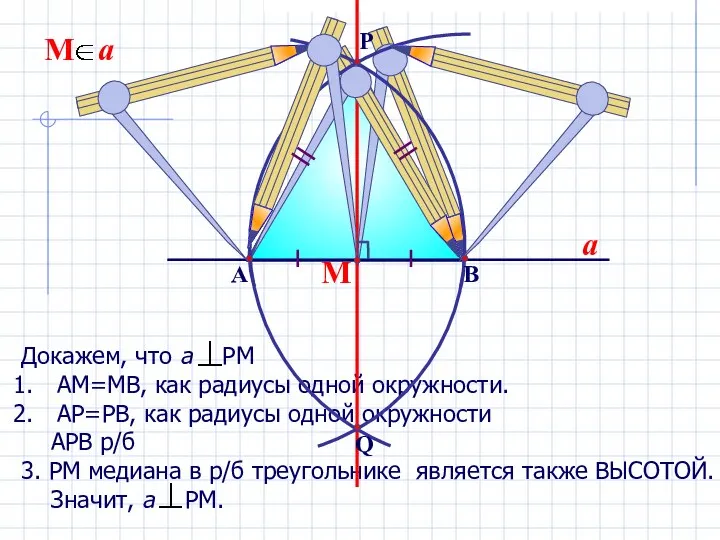
- 8. Докажем, что а РМ АМ=МВ, как радиусы одной окружности. АР=РВ, как радиусы одной окружности АРВ р/б
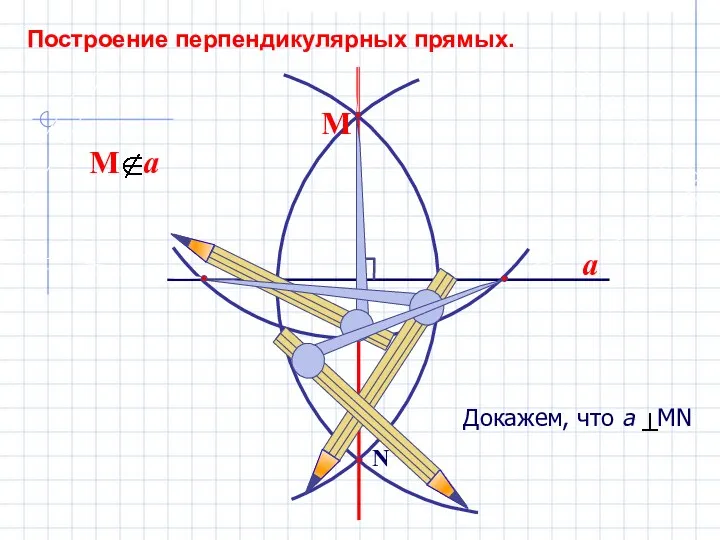
- 9. a N М Построение перпендикулярных прямых.
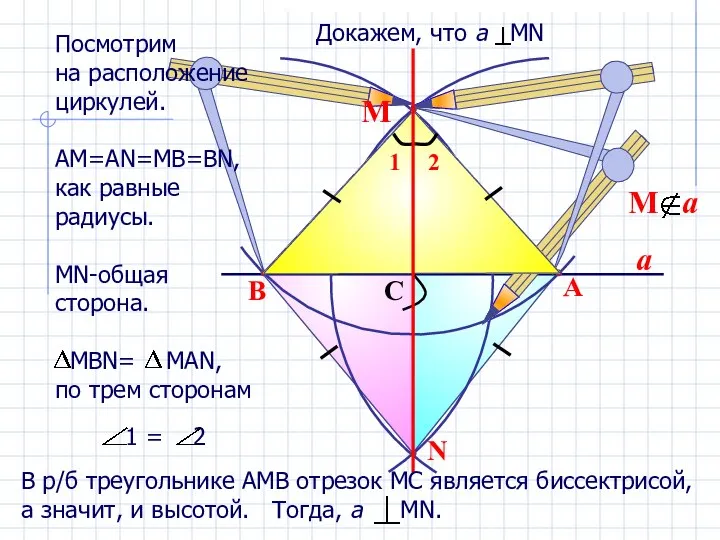
- 10. a N B A C М Посмотрим на расположение циркулей. АМ=АN=MB=BN, как равные радиусы. МN-общая сторона.
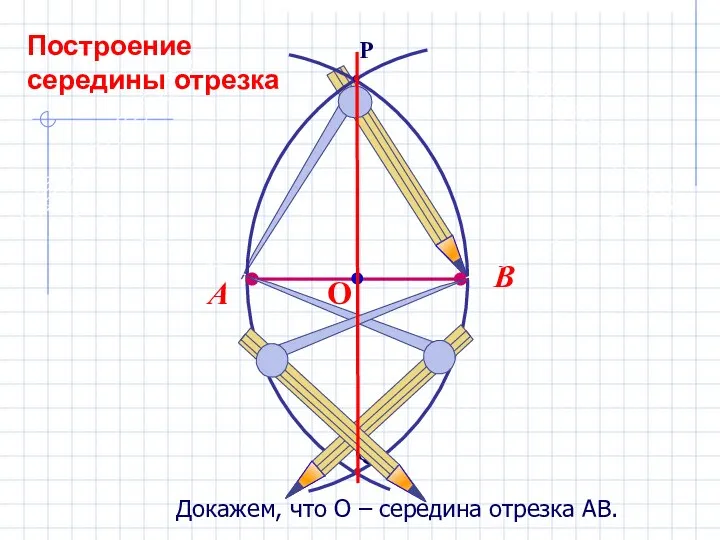
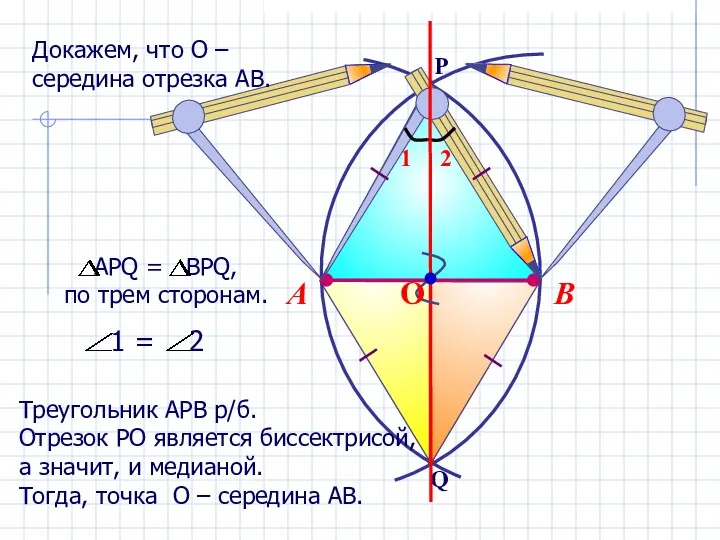
- 11. Докажем, что О – середина отрезка АВ. Построение середины отрезка
- 12. В А Треугольник АРВ р/б. Отрезок РО является биссектрисой, а значит, и медианой. Тогда, точка О
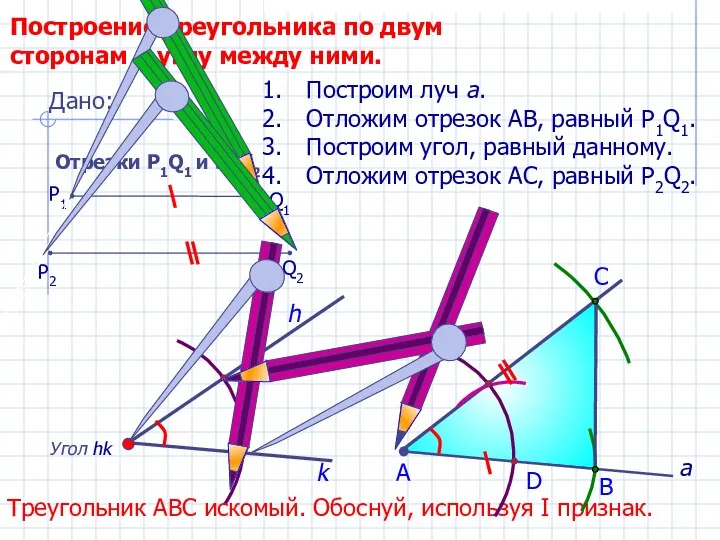
- 13. D С Построение треугольника по двум сторонам и углу между ними. Угол hk h Построим луч
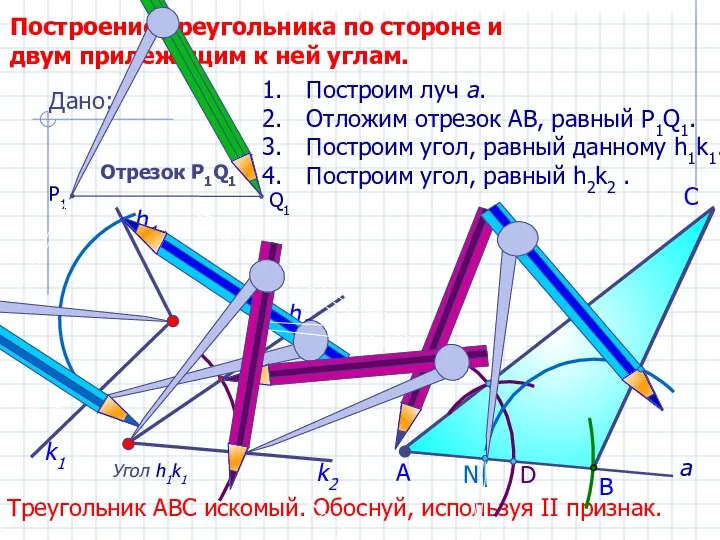
- 14. D С Построение треугольника по стороне и двум прилежащим к ней углам. Угол h1k1 h2 Построим
- 16. Скачать презентацию

 Рисуем на уроке математики Урок математики в 6 классе Автор: Вартанова Нелли Александровна учитель математики МОУ СОШ№19 ст.Ладож
Рисуем на уроке математики Урок математики в 6 классе Автор: Вартанова Нелли Александровна учитель математики МОУ СОШ№19 ст.Ладож Задачи и методы оптимального планирования
Задачи и методы оптимального планирования Свойства степени с натуральным показателем
Свойства степени с натуральным показателем Метод Гаусса решения систем линейных уравнений
Метод Гаусса решения систем линейных уравнений  Свойства вычитания
Свойства вычитания Уравнения в школьном курсе средней школы. 5-6 класс
Уравнения в школьном курсе средней школы. 5-6 класс Презентация по математике "Смежные углы" - скачать бесплатно
Презентация по математике "Смежные углы" - скачать бесплатно Множества и функции
Множества и функции Регулятивные удд
Регулятивные удд Отрезок. Треугольник. Многоугольники
Отрезок. Треугольник. Многоугольники Расширение множества натуральных чмсел
Расширение множества натуральных чмсел Презентация на тему Диаграммы 4 класс
Презентация на тему Диаграммы 4 класс Презентация на тему Сокращение дробей Математика, 6 класс
Презентация на тему Сокращение дробей Математика, 6 класс  История введения понятия функции в школьный курс математики и современность
История введения понятия функции в школьный курс математики и современность Презентация по математике "Натуральные числа" - скачать
Презентация по математике "Натуральные числа" - скачать  24.02.2010г. Дифференцирование частного и степени. Дернова А.М. учитель математики Iкв.к. МБОУ «Новотроицкая СОШ»
24.02.2010г. Дифференцирование частного и степени. Дернова А.М. учитель математики Iкв.к. МБОУ «Новотроицкая СОШ» Вклад мусульманских ученых в развитие геометрии и тригонометрии
Вклад мусульманских ученых в развитие геометрии и тригонометрии Комплексные числа
Комплексные числа Треугольник и его виды
Треугольник и его виды Применение распределительного свойства умножения
Применение распределительного свойства умножения Производная интеграла по переменному верхнему пределу
Производная интеграла по переменному верхнему пределу Задания по геометрии
Задания по геометрии Математика. Основы школьного стандарта
Математика. Основы школьного стандарта Презентация на тему Производная и интеграл
Презентация на тему Производная и интеграл  Проценты. 5 класс
Проценты. 5 класс Математическая игра-викторина. (6-7 класс)
Математическая игра-викторина. (6-7 класс) Математические основы манипулирования реляционными данными
Математические основы манипулирования реляционными данными Реальная математика
Реальная математика