Содержание
- 2. Взаимное расположение 2-х точек (x1, y1) и (x2, y2) относительно прямой ax + by + c
- 3. Угол α между векторами (x1, y1) и (x2, y2) Геометрические основы отсечения .
- 4. Пересечение прямых Геометрические основы отсечения если одна из прямых вертикальна (x = x0) или горизонтальна (y
- 5. Определение порядка обхода точек Геометрические основы отсечения
- 6. Определение выпуклости полигона Геометрические основы отсечения
- 7. Взаимное расположение точки и полигона (отсечение точки) Геометрические основы отсечения
- 8. Отсечение Алгоритм Коэна-Сазерленда отсечения отрезка
- 9. Отсечение Алгоритм отсечения отрезка выпуклым окном
- 10. Отсечение Разбиение невыпуклых многоугольников на выпуклые
- 11. Отсечение Отсечение многоугольников Алгоритм Сазерденда-Ходжмана отсечения выпуклым окном
- 12. Отсечение Отсечение многоугольников Алгоритм Вейлера-Азертона
- 13. Проективные преобразования (проекции) Проекция – это преобразование точек пространства размерности N в точки пространства размерности меньшей,
- 14. Проективные преобразования (проекции) Плоские геометрические проекции можно разделить на центральные и параллельные. Различие между ними определяется
- 15. Проективные преобразования (проекции). Центральная проекция
- 16. Проективные преобразования (проекции). Параллельная проекция
- 17. Проективные преобразования (проекции). Классификация
- 18. Параллельные ортографические проекции Если в параллельной проекции направление проецирования является нормалью к проекционной плоскости, то такая
- 19. Параллельные ортографические проекции. Математический аппарат
- 20. Параллельные аксонометрические проекции В случае аксонометрических проекций используются проекционные плоскости, не перпендикулярные главным координатным осям. На
- 21. Параллельные аксонометрические проекции. Изометрия В прямоугольной изометрической проекции аксонометрические оси образуют между собой углы в 120°,
- 22. Параллельные аксонометрические проекции. Диметрия В прямоугольной диметрической проекции ось Z', как и в предыдущем случае, расположена
- 23. Параллельные аксонометрические проекции. Триметрия В триметрической проекции коэффициенты искажения по всем трем осям, а также углы,
- 24. Параллельные аксонометрические проекции. Математический аппарат Пусть проекционная плоскость задается единичным вектором нормали и расстоянием от начала
- 25. Параллельные аксонометрические проекции. Математический аппарат. Шаг 1 1. Сдвиг на вектор с помощью матрицы
- 26. Параллельные аксонометрические проекции. Математический аппарат. Шаг 2 2. Поворот, совмещающий направление нормали с направлением оси OZ
- 27. Параллельные аксонометрические проекции. Математический аппарат. Шаг 3 3. Проекция на плоскость XOY с помощью матрицы
- 28. Параллельные аксонометрические проекции. Математический аппарат. Шаги 4-5 4. Поворот с помощью матрицы R-1 5. Сдвиг на
- 29. Параллельные косоугольные проекции Косоугольные (наклонные) проекции сочетают в себе свойства ортографических проекций со свойствами аксонометрии. Проекционная
- 30. Параллельные косоугольные проекции. Проекция Кавалье В проекции Кавалье направление проецирования составляет с плоскостью угол 45°. В
- 31. Параллельные косоугольные проекции. Кабинетная проекция В кабинетной проекции (рис. 7.8) направление проецирования составляет с плоскостью угол
- 32. Параллельные косоугольные проекции. Математический аппарат
- 33. Центральные проекции Когда пучок проекторов исходит из заданного центра, то отрезки, бывшие изначально параллельными, на плоскости
- 34. Центральные проекции. Одноточечная проекция
- 35. Центральные проекции. Двухточечная проекция
- 36. Центральные проекции. Трехточечная проекция
- 37. Центральные проекции. Математический аппарат c1 – расстояние от наблюдателя (точки схода лучей) до проекционной плоскости
- 39. Скачать презентацию




































 Построение эпюров плоскости и точки, прямой, принадлежащей этой плоскости
Построение эпюров плоскости и точки, прямой, принадлежащей этой плоскости Общие правила выполнения чертежей
Общие правила выполнения чертежей Плоскости и их проекции
Плоскости и их проекции Теоретический чертёж корпуса судна
Теоретический чертёж корпуса судна Резьбы. Резьбовые изделия и соединения. Лекция 3
Резьбы. Резьбовые изделия и соединения. Лекция 3 Демонстрационный отчет по результатам измерений для ООО МЗ Тонар
Демонстрационный отчет по результатам измерений для ООО МЗ Тонар Линии чертежа
Линии чертежа Соединение вида и разреза
Соединение вида и разреза Нанесение размеров
Нанесение размеров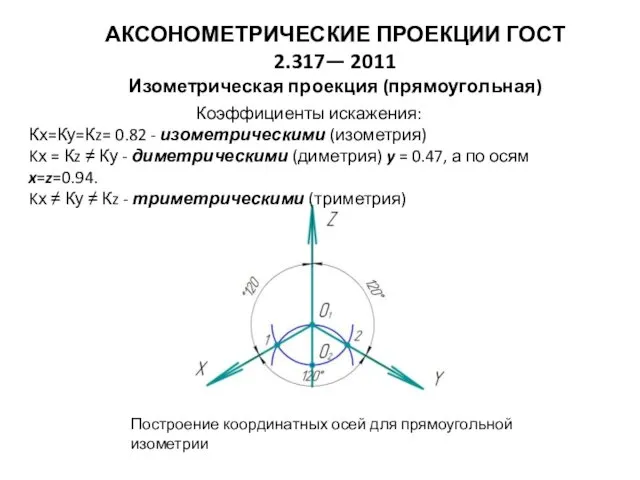 Аксонометрические проекции ГОСТ 2.317— 2011
Аксонометрические проекции ГОСТ 2.317— 2011 Аксонометрические проекции плоских геометрических фигур
Аксонометрические проекции плоских геометрических фигур Графические работы
Графические работы Классификация поверхностей
Классификация поверхностей Черчение. Оформление чертежа
Черчение. Оформление чертежа Тема 1.1 . Основные сведения по оформлению чертежей
Тема 1.1 . Основные сведения по оформлению чертежей Обозначения графических материалов и правила их нанесения на чертежах
Обозначения графических материалов и правила их нанесения на чертежах Изображения – виды, разрезы, сечения. Лекция 6
Изображения – виды, разрезы, сечения. Лекция 6 Расчетные длины элементов стальных конструкций
Расчетные длины элементов стальных конструкций Выполнение соединения шпилькой
Выполнение соединения шпилькой Проекционное черчение
Проекционное черчение Шрифт чертёжный
Шрифт чертёжный Геометрическое черчение
Геометрическое черчение Пересечение поверхностей плоскостями
Пересечение поверхностей плоскостями Проекционные задачи на эпюре Монжа
Проекционные задачи на эпюре Монжа Технический рисунок
Технический рисунок Проецирование правильных треугольных и шестиугольных призм
Проецирование правильных треугольных и шестиугольных призм Линии. Сплошная толстая основная
Линии. Сплошная толстая основная Пересечение поверхностей с вращением
Пересечение поверхностей с вращением