Базовые геометрические элементы начертательной геометрии

Слайд 4

Точка – абстрактное математическое понятие. Нульмерный объект (не имеет измерений).
Линия –

непрерывное одномерное множество точек ( цепочка точек). Измерение : только длина. Толщины нет.
Поверхность – непрерывное двумерное множество точек. Измерения : длина, ширина, площадь. Толщины и объема нет.

Слайд 5

Проективное пространство

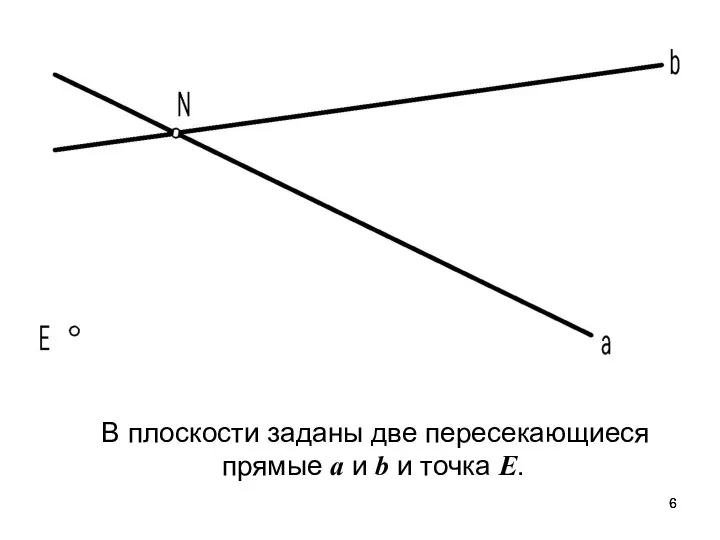
Слайд 6

В плоскости заданы две пересекающиеся прямые a и b и

точка E.

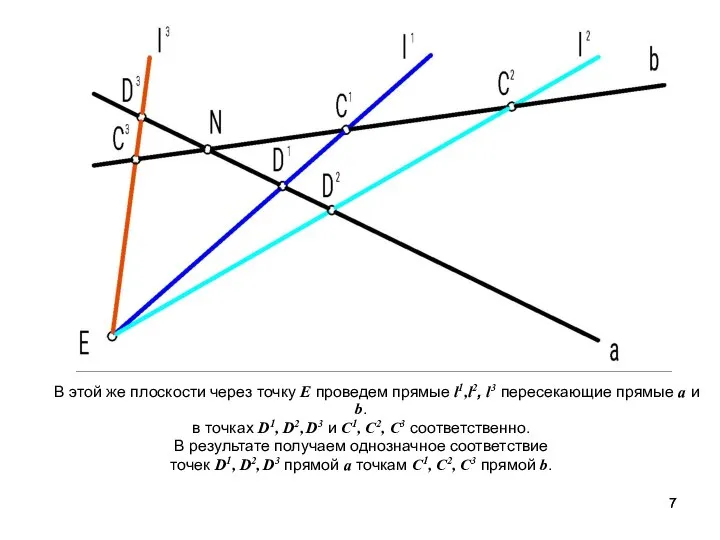
Слайд 7

В этой же плоскости через точку Е проведем прямые l1,l2,

l3 пересекающие прямые a и b.
в точках D1, D2, D3 и C1, C2, C3 соответственно.
В результате получаем однозначное соответствие
точек D1, D2, D3 прямой a точкам C1, C2, C3 прямой b.

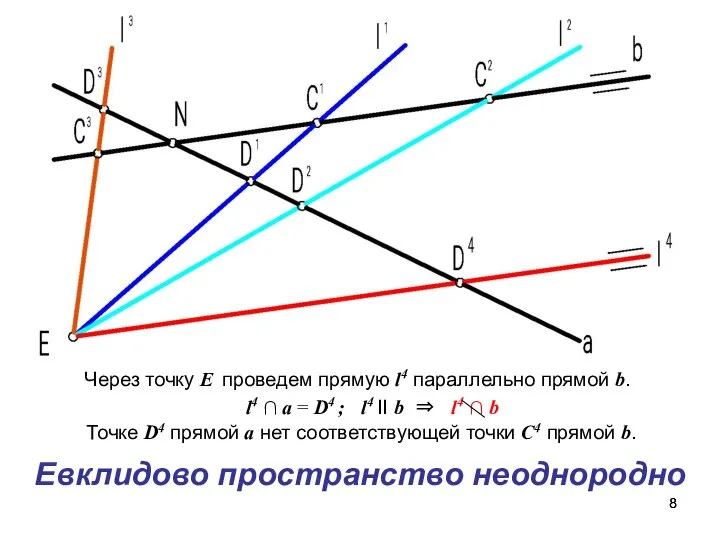
Слайд 8

Через точку Е проведем прямую l4 параллельно прямой b.
l4

∩ a = D4 ; l4 II b ⇒ l4 ∩ b
Точке D4 прямой a нет соответствующей точки C4 прямой b.

Евклидово пространство неоднородно

Слайд 9

Для устранения неоднородности Евклидова пространства
(m || n) ⇒

(m ∩ n = F∞ )

условно принято,

что параллельные между собой прямые
пересекаются
в бесконечно удаленной точке F∞ -

несобственной точке пространства.

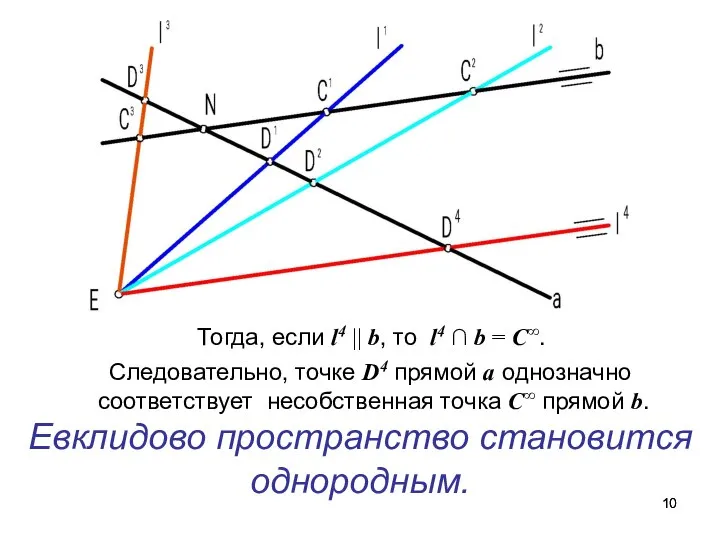
Слайд 10

Тогда, если l4 || b, то l4 ∩ b =

С∞.
Следовательно, точке D4 прямой a однозначно соответствует несобственная точка С∞ прямой b.

Евклидово пространство становится однородным.

Слайд 11

Евклидово пространство, дополненное несобственными элементами,
называют проективным.

Слайд 12

Метод проецирования

Слайд 13

Все изображения разные, но их объединяет то, что в основе их

построения лежит один и тот же метод – метод проецирования.
Все изображения, построенные на основе метода проецирования, называются проекционными

Перспективная проекция

Аксонометрическая проекция

Ортогональные проекции

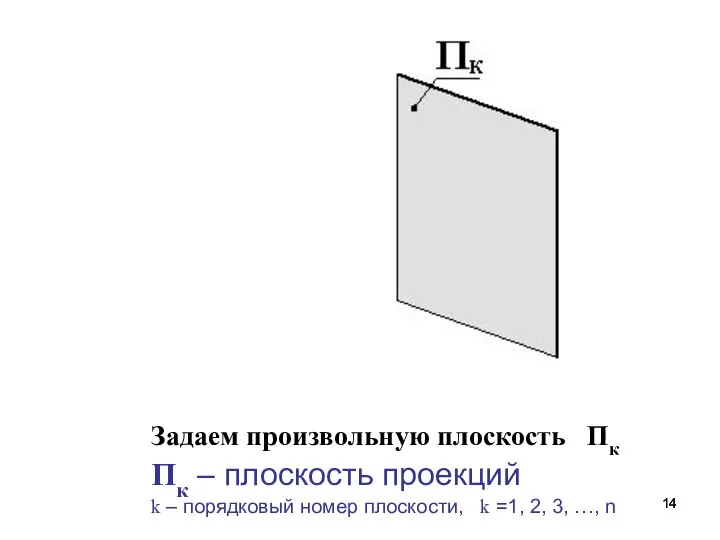
Слайд 14

Задаем произвольную плоскость Пк
Пк – плоскость проекций
k –

порядковый номер плоскости, k =1, 2, 3, …, n

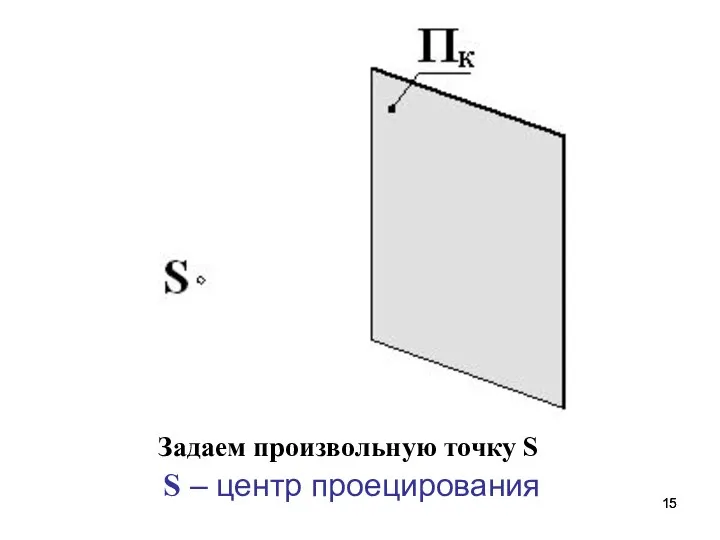
Слайд 15

Задаем произвольную точку S
S – центр проецирования

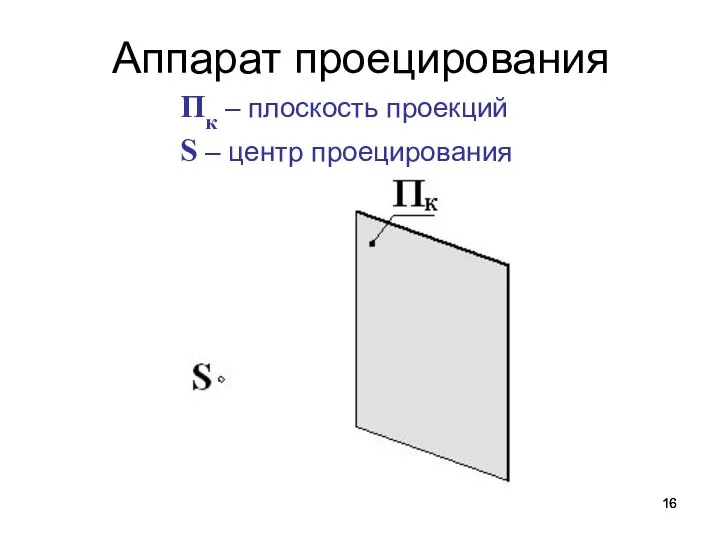
Слайд 16

Аппарат проецирования
Пк – плоскость проекций
S – центр проецирования

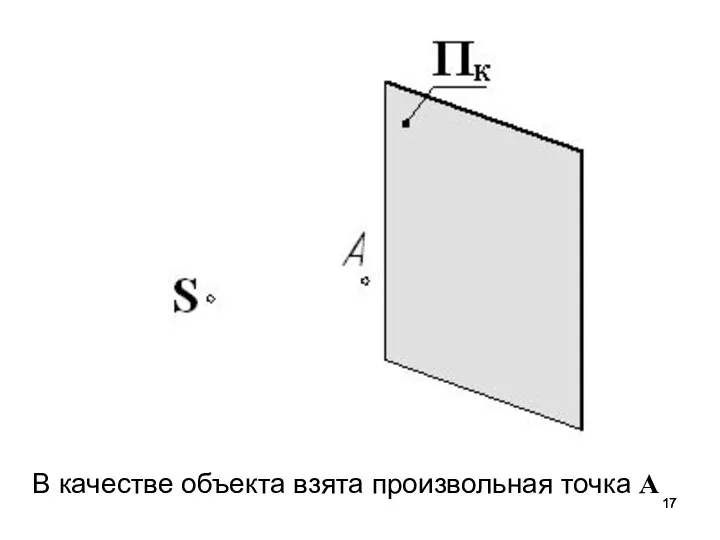
Слайд 17

В качестве объекта взята произвольная точка А

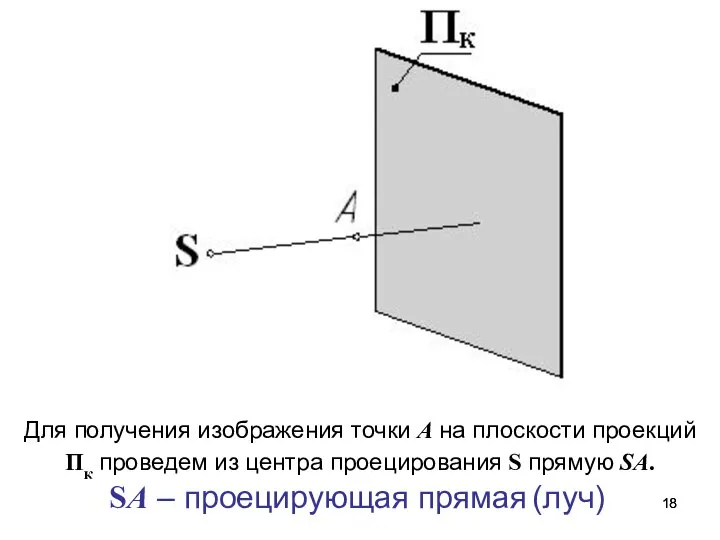
Слайд 18

Для получения изображения точки А на плоскости проекций Пк проведем из

центра проецирования S прямую SA.
SA – проецирующая прямая (луч)

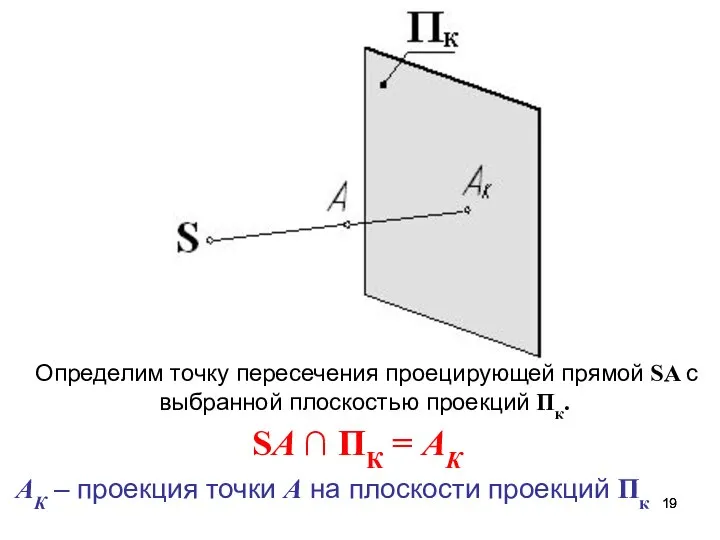
Слайд 19

Определим точку пересечения проецирующей прямой SA с выбранной плоскостью проекций Пк.
SA

∩ ПК = АК

АК – проекция точки А на плоскости проекций Пк

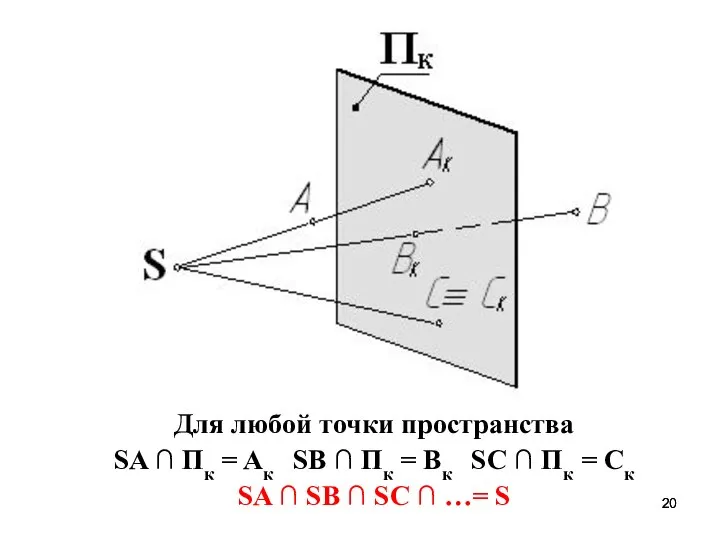
Слайд 20

Для любой точки пространства
SA ∩ Пк = Aк SВ ∩

Пк = Bк SС ∩ Пк = Cк
SA ∩ SВ ∩ SС ∩ …= S

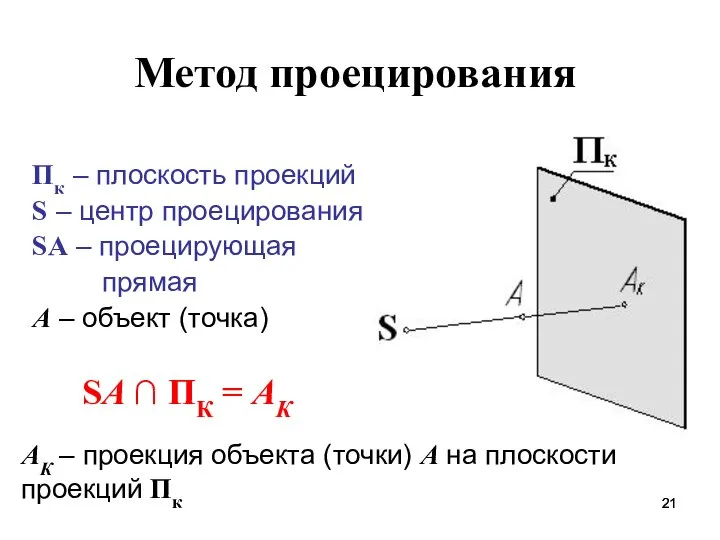
Слайд 21

Пк – плоскость проекций
S – центр проецирования
SA – проецирующая
прямая
А

– объект (точка)

Метод проецирования

SA ∩ ПК = АК

АК – проекция объекта (точки) А на плоскости проекций Пк

Слайд 22

Варианты метода проецирования

Слайд 23

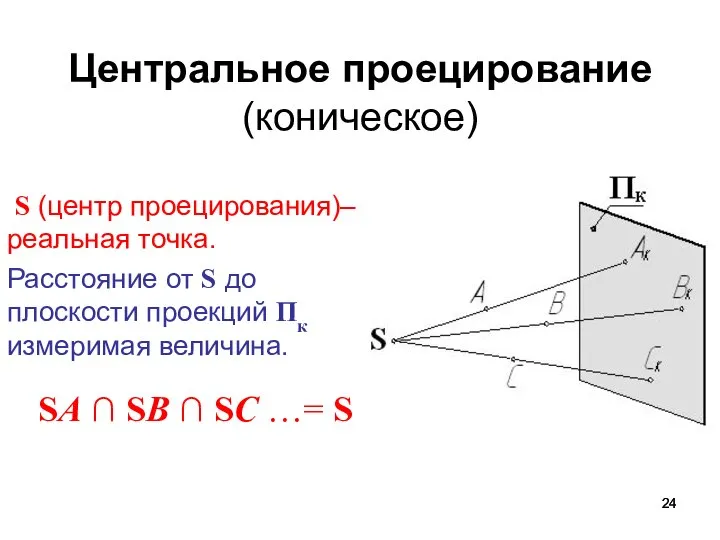
Слайд 24

Центральное проецирование (коническое)
S (центр проецирования)– реальная точка.
Расстояние от S до

плоскости проекций Пк измеримая величина.

SA ∩ SB ∩ SC …= S

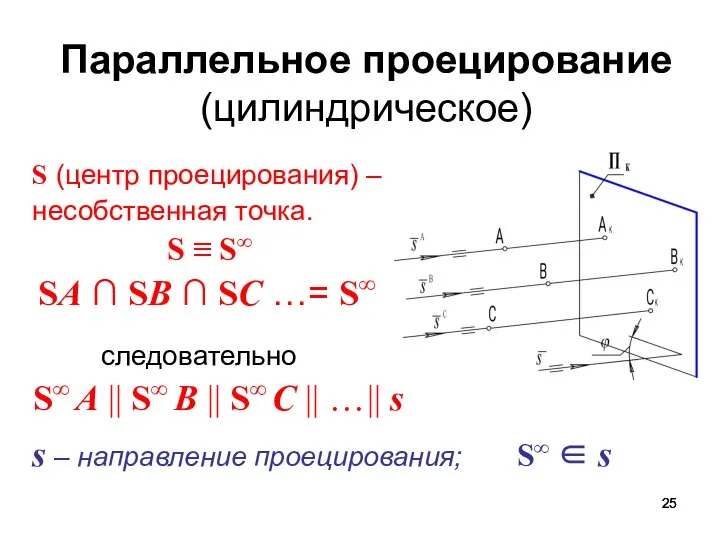
Слайд 25

Параллельное проецирование (цилиндрическое)
S (центр проецирования) –
несобственная точка.
S ≡ S∞
SA

∩ SB ∩ SC …= S∞

следовательно
S∞ A || S∞ B || S∞ C || …

s – направление проецирования; S∞ ∈ s

|| s

Слайд 26

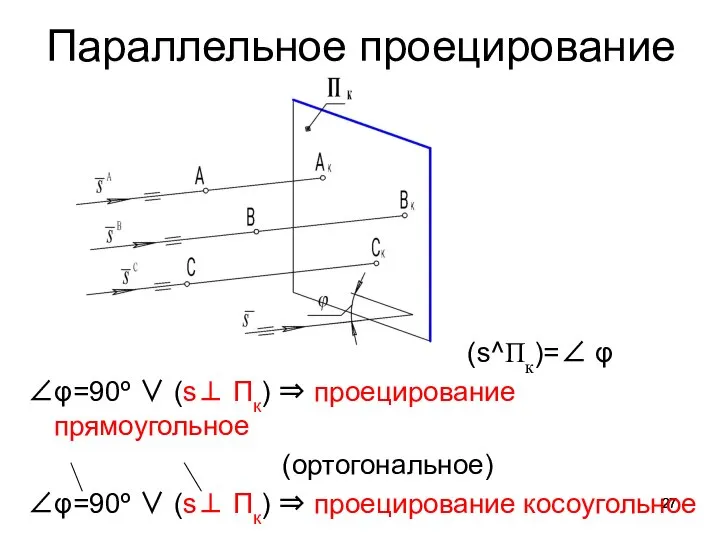
Слайд 27

Параллельное проецирование
(s^Пк)=∠ φ
∠φ=90º ∨ (s⊥ Пк) ⇒ проецирование прямоугольное

(ортогональное)
∠φ=90º ∨ (s⊥ Пк) ⇒ проецирование косоугольное

Слайд 28

Слайд 29

Свойства проецирования

Слайд 30

Общие свойства проецирования

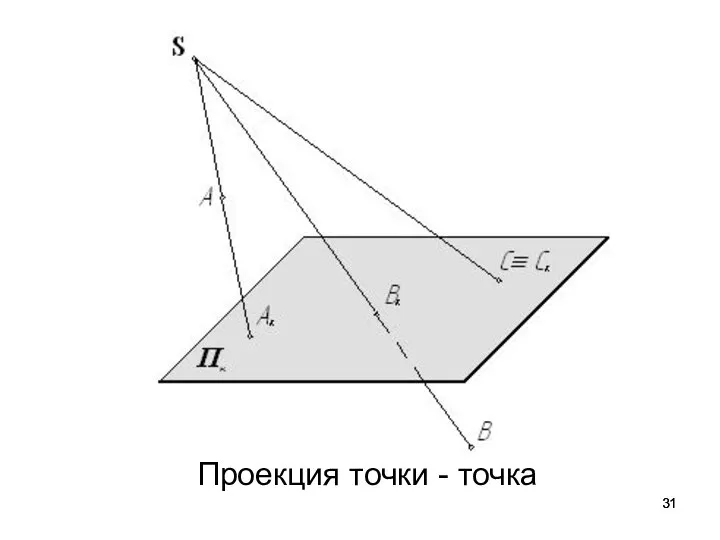
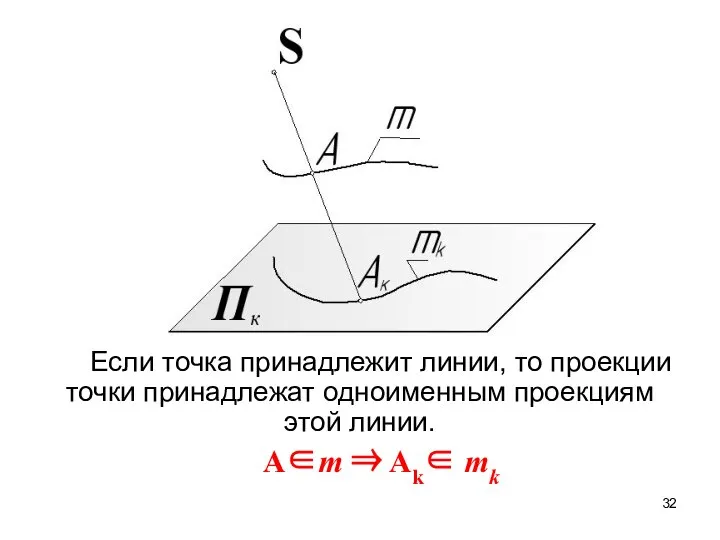
Слайд 31

Проекция точки - точка

Слайд 32

Если точка принадлежит линии, то проекции точки принадлежат одноименным проекциям этой

линии.
A∈m ⇒ Ak∈ mk

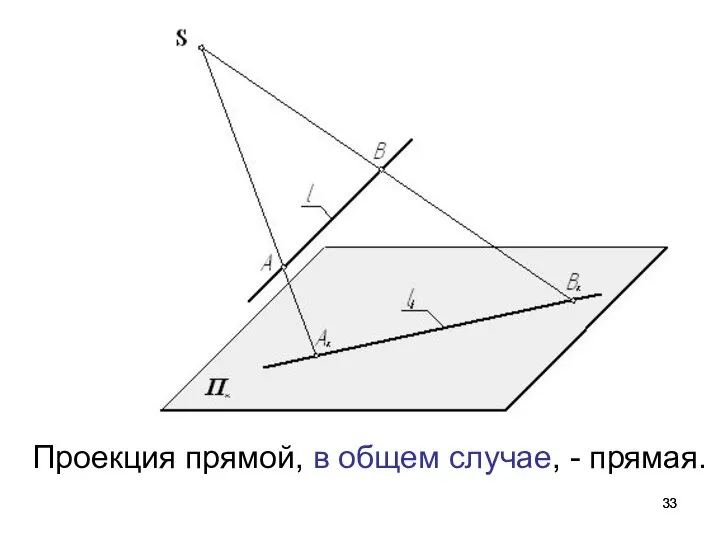
Слайд 33

Проекция прямой, в общем случае, - прямая.

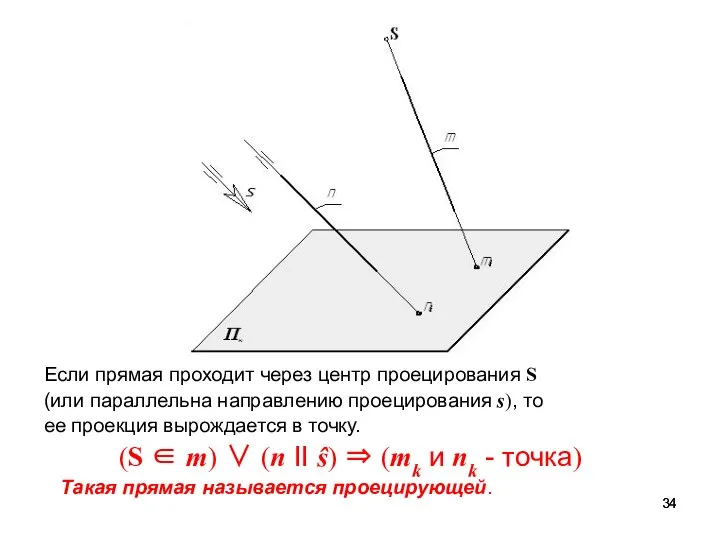
Слайд 34

Если прямая проходит через центр проецирования S
(или параллельна направлению проецирования

s), то
ее проекция вырождается в точку.
(S ∈ m) ∨ (n II ŝ) ⇒ (mk и nk - точка)
Такая прямая называется проецирующей.

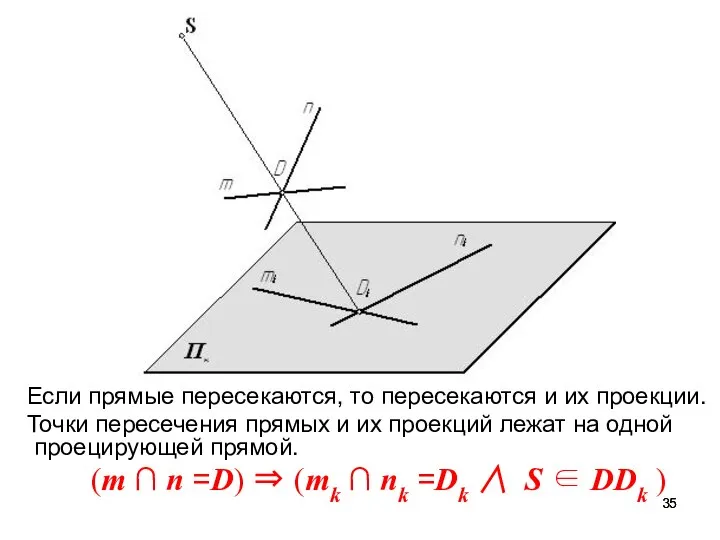
Слайд 35

Если прямые пересекаются, то пересекаются и их проекции.
Точки пересечения

прямых и их проекций лежат на одной проецирующей прямой.
(m ∩ n =D) ⇒ (mk ∩ nk =Dk ∧ S ∈ DDk )

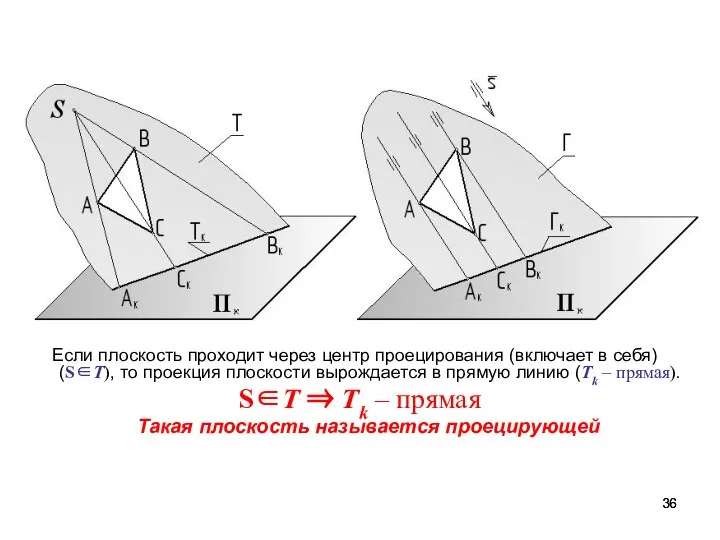
Слайд 36

Если плоскость проходит через центр проецирования (включает в себя) (S∈Т),

то проекция плоскости вырождается в прямую линию (Тk – прямая).
S∈Т ⇒ Тk – прямая
Такая плоскость называется проецирующей

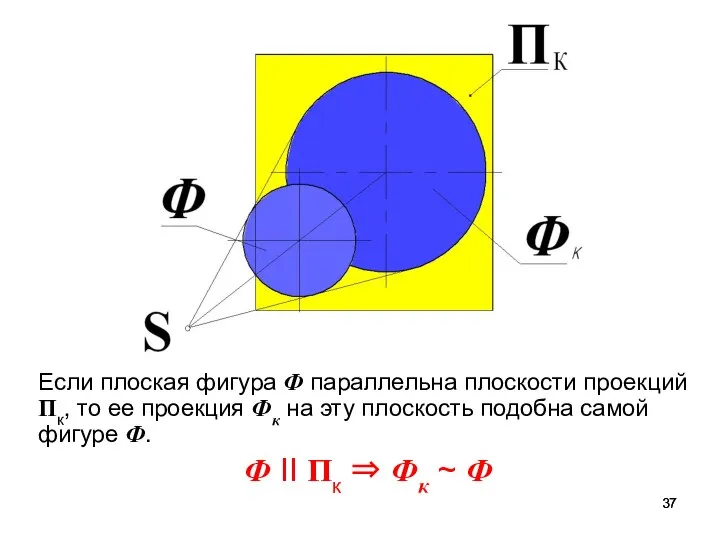
Слайд 37

Если плоская фигура Ф параллельна плоскости проекций Пк, то ее проекция

Фк на эту плоскость подобна самой фигуре Ф.
Ф II Пк ⇒ Фк ~ Ф

Слайд 38

Инвариантные свойства параллельного проецирования

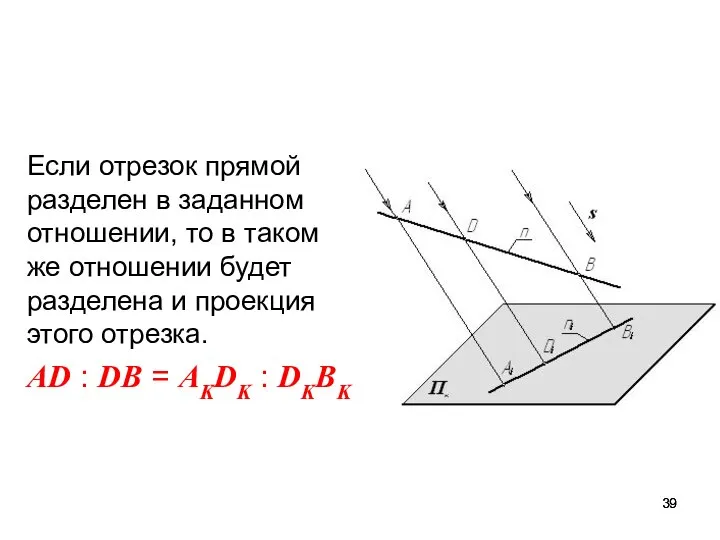
Слайд 39

Если отрезок прямой разделен в заданном отношении, то в таком же

отношении будет разделена и проекция этого отрезка.
AD : DB = AKDK : DKBK

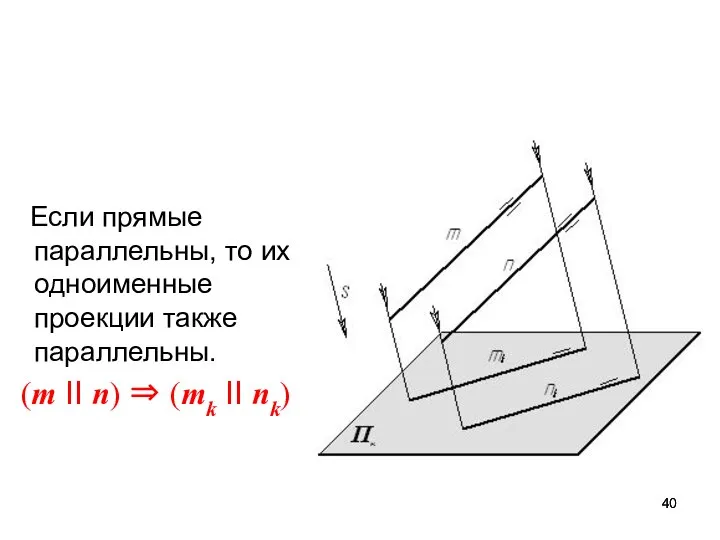
Слайд 40

Если прямые параллельны, то их одноименные проекции также параллельны.
(m

II n) ⇒ (mk II nk)

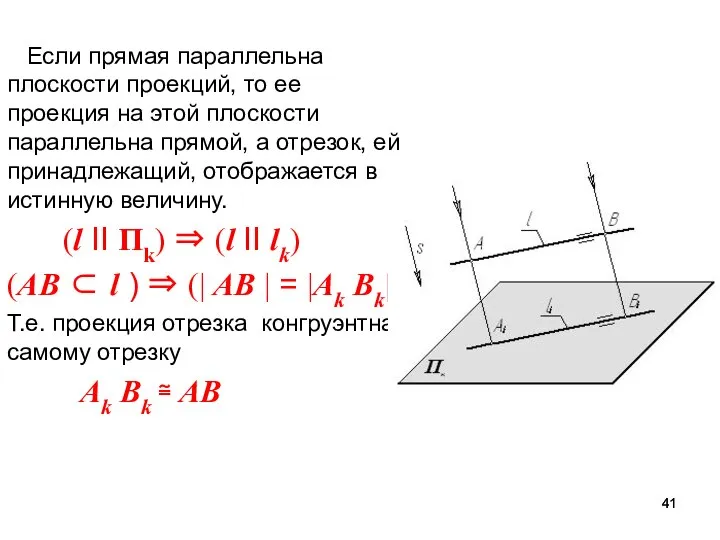
Слайд 41

Если прямая параллельна плоскости проекций, то ее проекция на этой

плоскости параллельна прямой, а отрезок, ей принадлежащий, отображается в истинную величину.
(l II Пk) ⇒ (l II lk)
(AB ⊂ l ) ⇒ (| AB | = |Ak Bk|)
Т.е. проекция отрезка конгруэнтна самому отрезку
Ak Bk ≅ AB

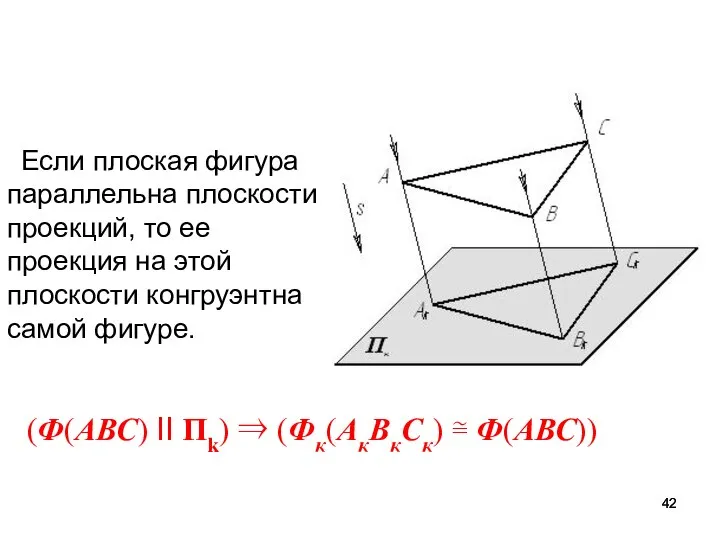
Слайд 42

Если плоская фигура параллельна плоскости проекций, то ее проекция на этой

плоскости конгруэнтна самой фигуре.

(Ф(АВС) II Пk) ⇒ (Фк(АкВкСк) ≅ Ф(АВС))

Слайд 43

Требования, предъявляемые к проекционному изображению

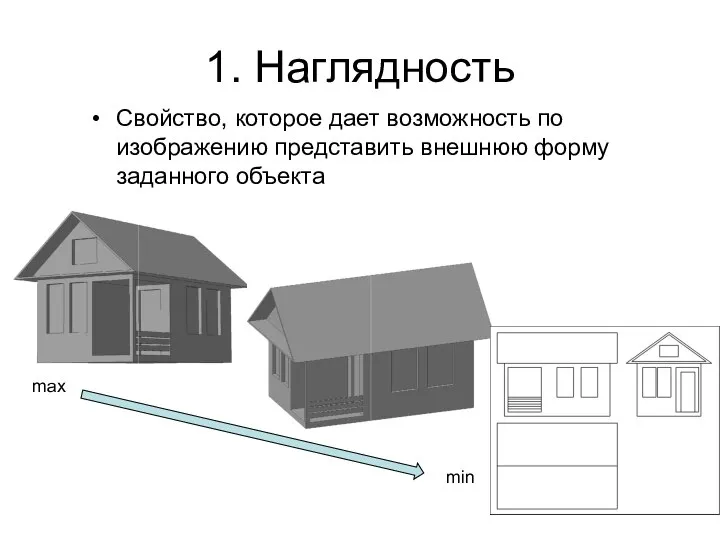
Слайд 44

1. Наглядность
Свойство, которое дает возможность по изображению представить внешнюю форму заданного

объекта

max

min

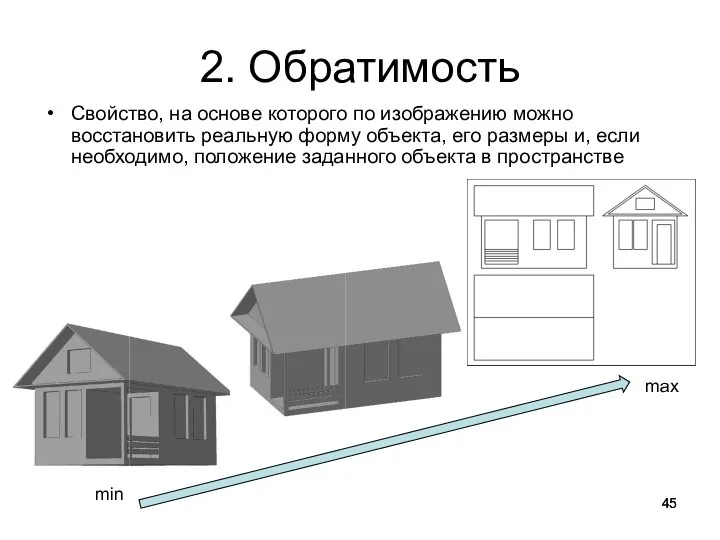
Слайд 45

2. Обратимость
Свойство, на основе которого по изображению можно восстановить реальную форму

объекта, его размеры и, если необходимо, положение заданного объекта в пространстве

min

max

Слайд 46

3. Единство правил построения изображения и правил его графического оформления

Слайд 47

Выбор того или иного вида проекции определяется функциональным назначением получаемого изображения.
Для

презентаций определяющим свойством является наглядность изображения (перспективная или аксонометрическая проекция).
Для разработки технологического процесса изготовления (строительства) объекта определяющим является обратимость изображения (ортогональные проекции).

Выводы

Слайд 48

Ортогональные проекции

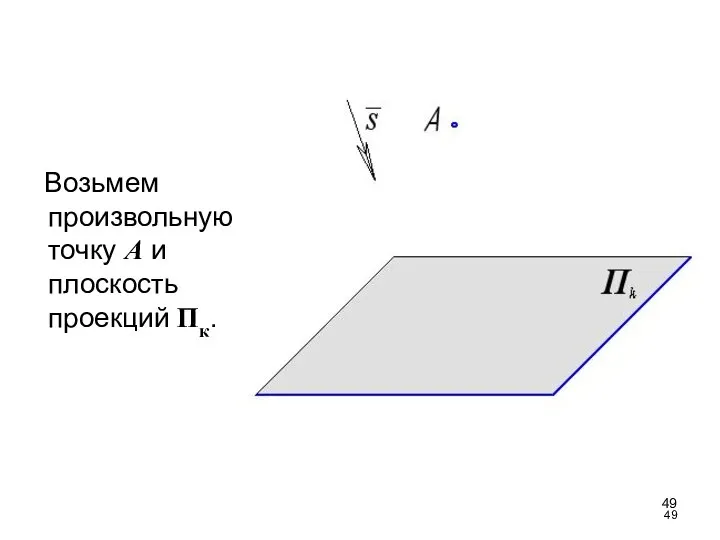
Слайд 49

Возьмем произвольную точку А и плоскость проекций Пк.

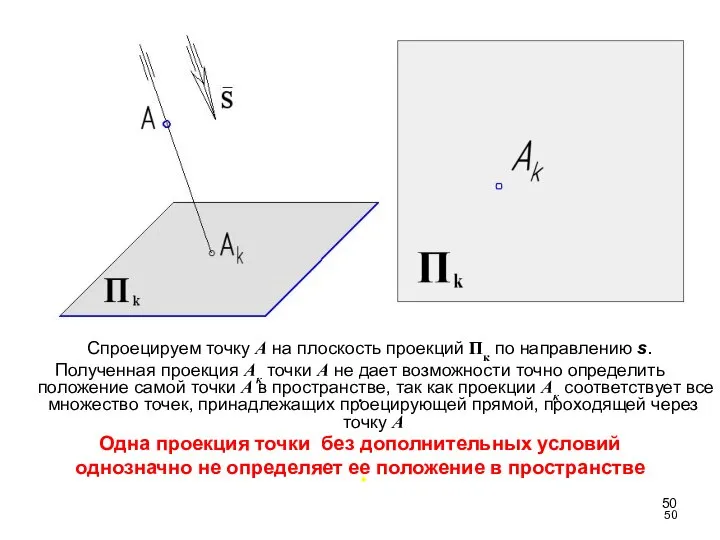
Слайд 50

Спроецируем точку А на плоскость проекций Пк по направлению s.
Полученная

проекция Ак точки А не дает возможности точно определить положение самой точки А в пространстве, так как проекции Ак соответствует все множество точек, принадлежащих проецирующей прямой, проходящей через точку А
Одна проекция точки без дополнительных условий
однозначно не определяет ее положение в пространстве

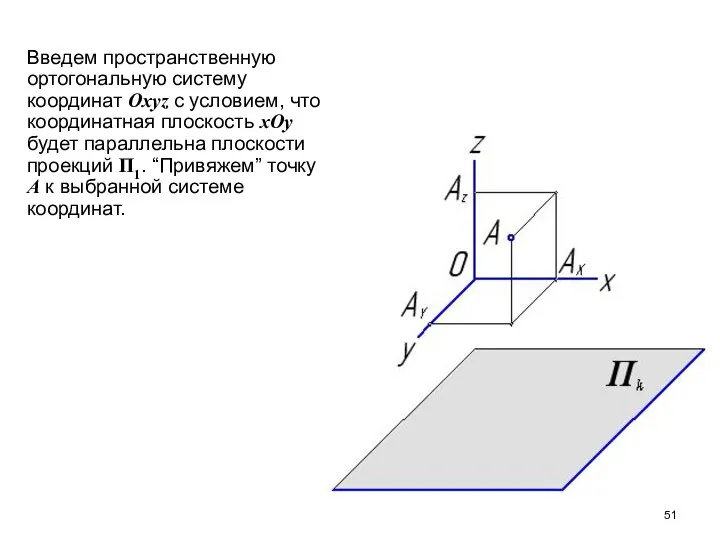
Слайд 51

Введем пространственную ортогональную систему координат Оxyz с условием, что координатная плоскость

хОу будет параллельна плоскости проекций П1. “Привяжем” точку А к выбранной системе координат.

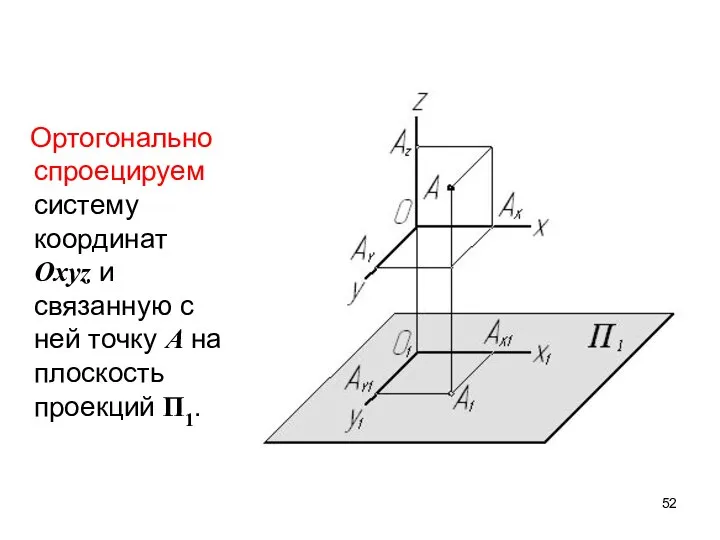
Слайд 52

Ортогонально спроецируем систему координат Oxyz и связанную с ней точку

А на плоскость проекций П1.

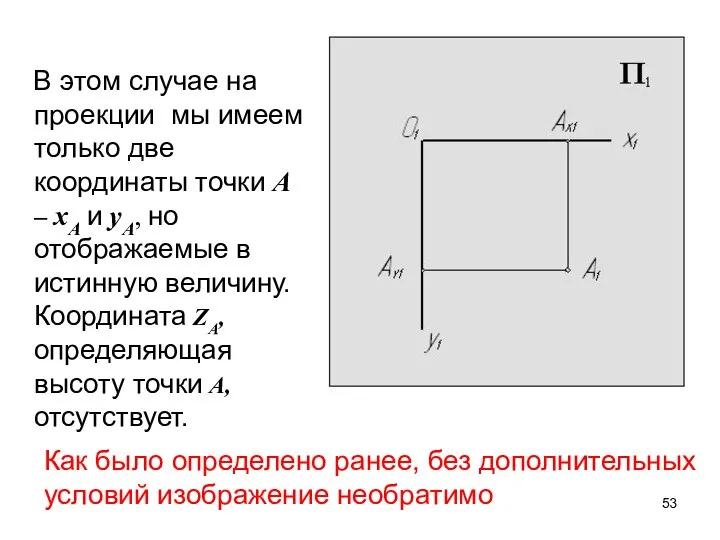
Слайд 53

В этом случае на проекции мы имеем только две координаты

точки А – xA и yA, но отображаемые в истинную величину. Координата ZA, определяющая высоту точки А, отсутствует.

Как было определено ранее, без дополнительных
условий изображение необратимо

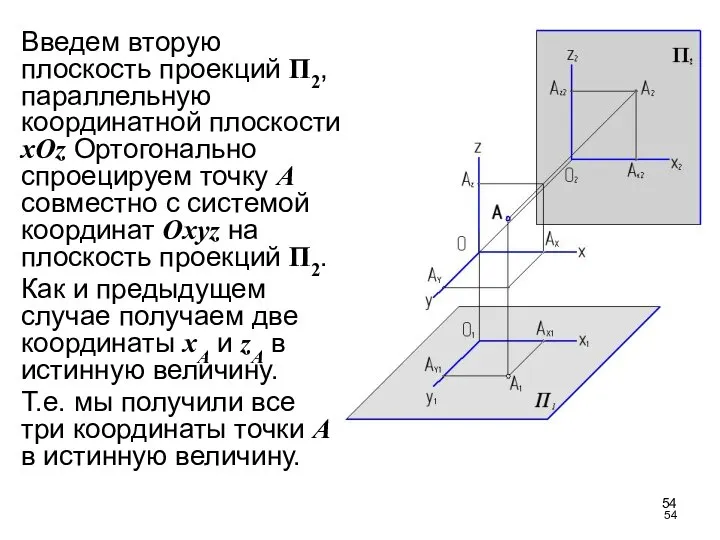
Слайд 54

Введем вторую плоскость проекций П2, параллельную координатной плоскости xOz Ортогонально спроецируем

точку А совместно с системой координат Oxyz на плоскость проекций П2.
Как и предыдущем случае получаем две координаты xA и zA в истинную величину.
Т.е. мы получили все три координаты точки А в истинную величину.

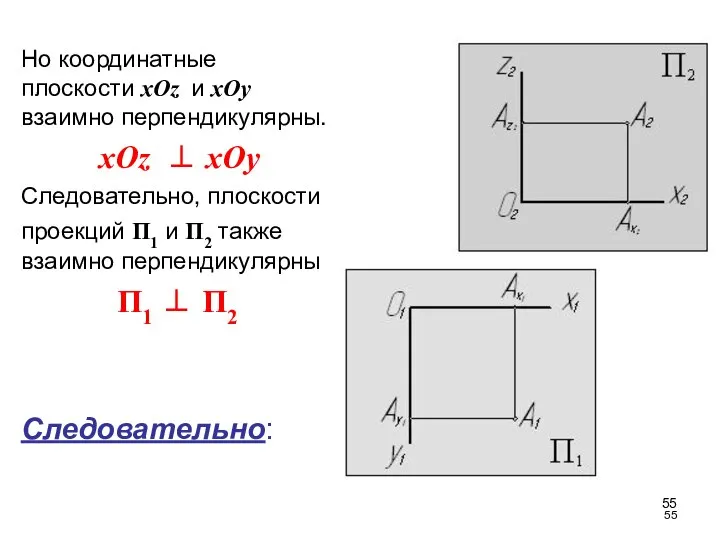
Слайд 55

Но координатные плоскости xOz и xOy взаимно перпендикулярны.
xOz ⊥ xOy
Следовательно,

плоскости проекций П1 и П2 также взаимно перпендикулярны
П1 ⊥ П2
Следовательно:

Слайд 56

Ортогональные проекции точки на две взаимно перпендикулярные плоскости проекций однозначно

определяют положение точки в пространстве и делают изображения обратимыми.

Слайд 57

Метод Монжа

Слайд 58

Ортогональная система двух плоскостей проекций

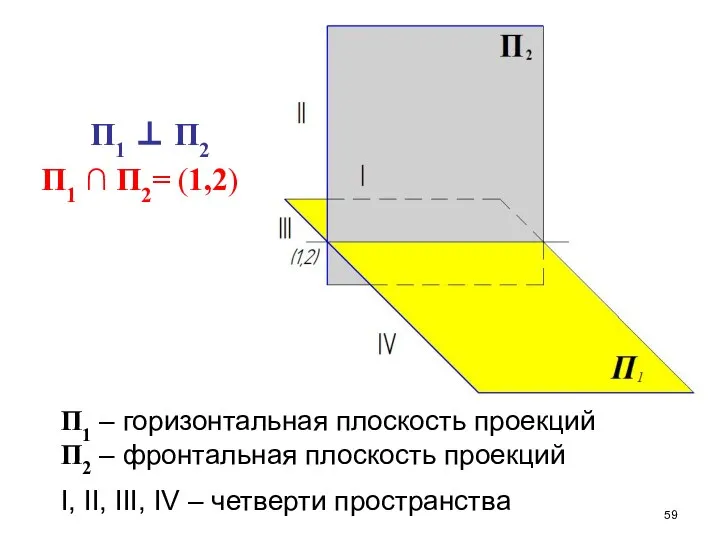
Слайд 59

П1 ⊥ П2
П1 ∩ П2= (1,2)
П1 – горизонтальная плоскость проекций
П2

– фронтальная плоскость проекций

I, II, III, IV – четверти пространства

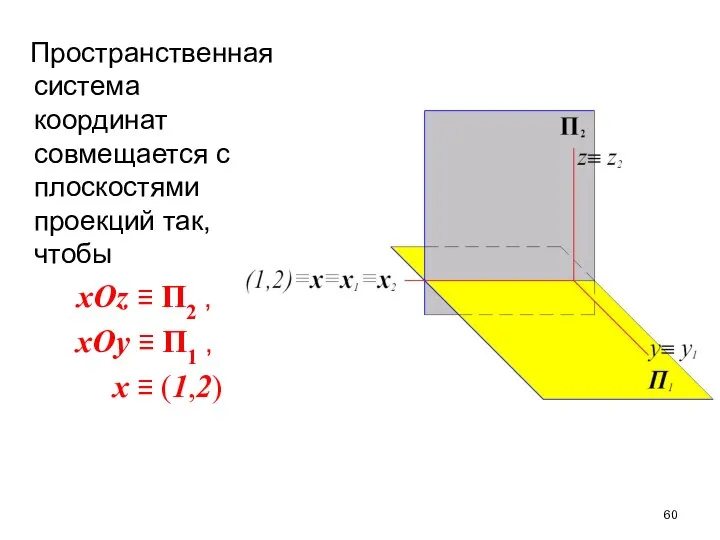
Слайд 60

Пространственная система координат совмещается с плоскостями проекций так, чтобы
xOz ≡

П2 ,
xOy ≡ П1 ,
x ≡ (1,2)

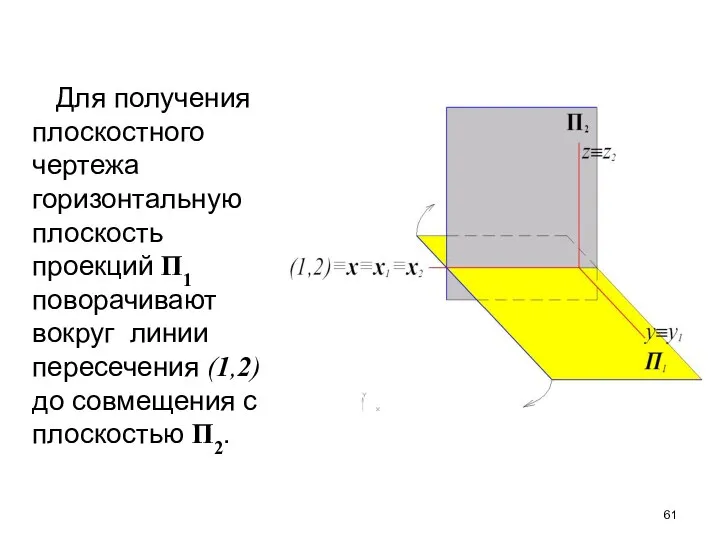
Слайд 61

Для получения плоскостного чертежа горизонтальную плоскость проекций П1 поворачивают вокруг

линии пересечения (1,2) до совмещения с плоскостью П2.

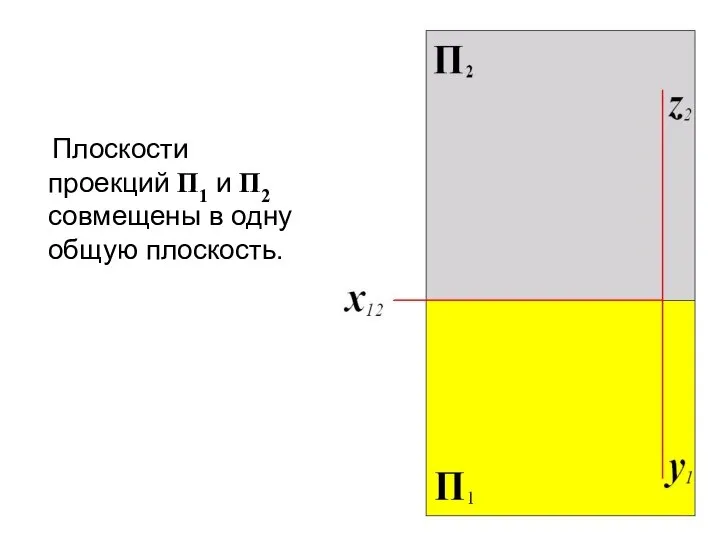
Слайд 62

Плоскости проекций П1 и П2 совмещены в одну общую плоскость.

Слайд 63

Так как плоскости проекций бесконечны, то их границы не оказывают.

Координатные оси y и z также не показывают.
В дальнейшем, когда не требуется знать положение объекта в пространстве относительно системы координат Oxyz, ось х1,2 также может не изображать-ся. Получаем безосную систему.

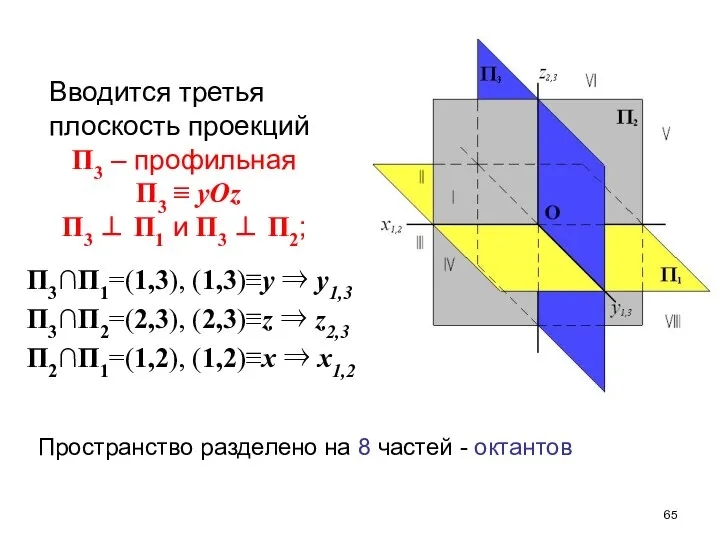
Слайд 64

Ортогональная система трех плоскостей проекций

Слайд 65

П3∩П1=(1,3), (1,3)≡y ⇒ y1,3
П3∩П2=(2,3), (2,3)≡z ⇒ z2,3
П2∩П1=(1,2), (1,2)≡x ⇒ x1,2
Вводится третья

плоскость проекций
П3 – профильная
П3 ≡ yOz
П3 ⊥ П1 и П3 ⊥ П2;

Пространство разделено на 8 частей - октантов

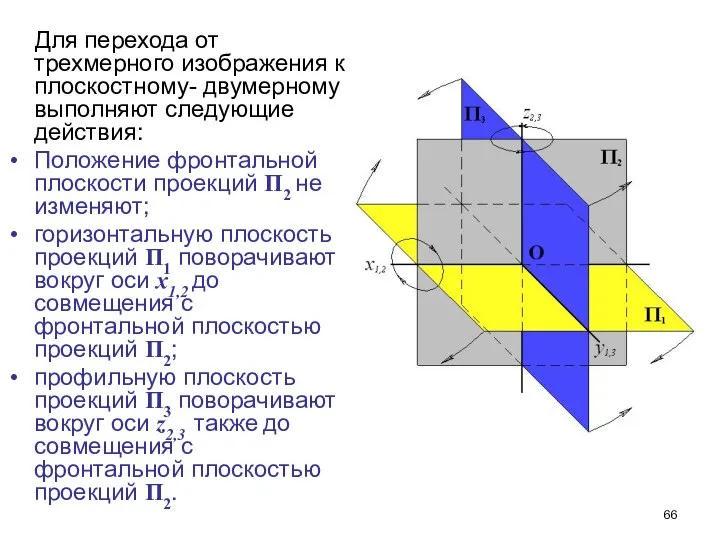
Слайд 66

Для перехода от трехмерного изображения к плоскостному- двумерному выполняют следующие

действия:
Положение фронтальной плоскости проекций П2 не изменяют;
горизонтальную плоскость проекций П1 поворачивают вокруг оси x1,2 до совмещения с фронтальной плоскостью проекций П2;
профильную плоскость проекций П3 поворачивают вокруг оси z2,3 также до совмещения с фронтальной плоскостью проекций П2.

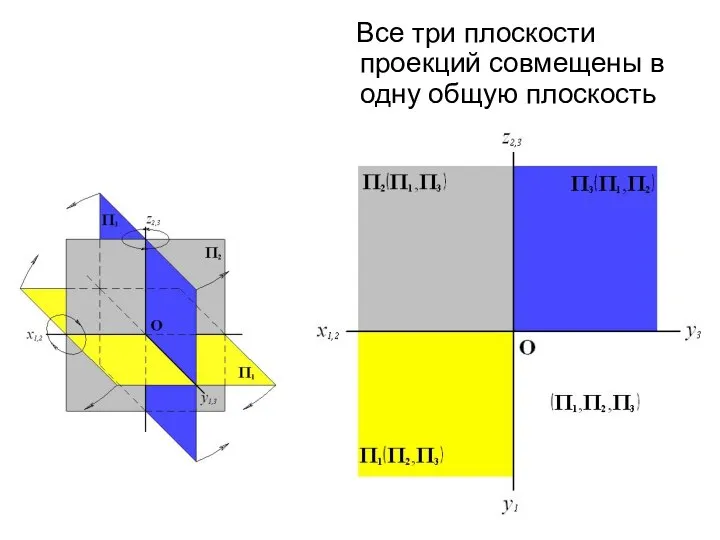
Слайд 67

Все три плоскости проекций совмещены в одну общую плоскость

Слайд 68

Проецирование точки

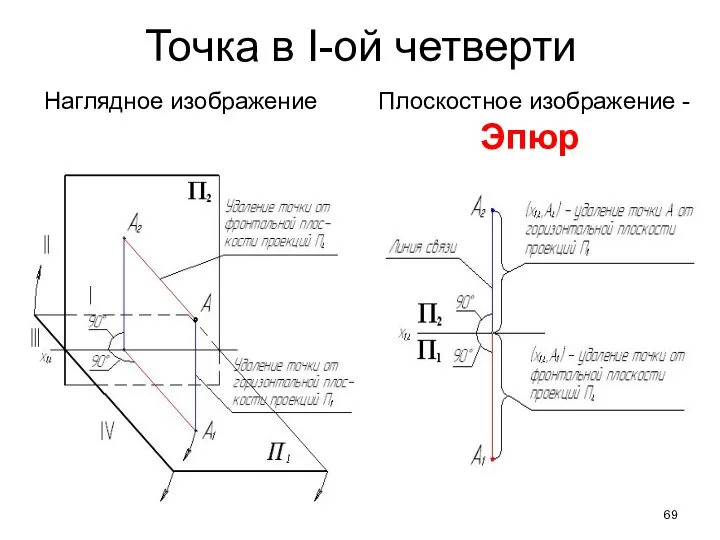
Слайд 69

Точка в I-ой четверти
Наглядное изображение
Плоскостное изображение -
Эпюр

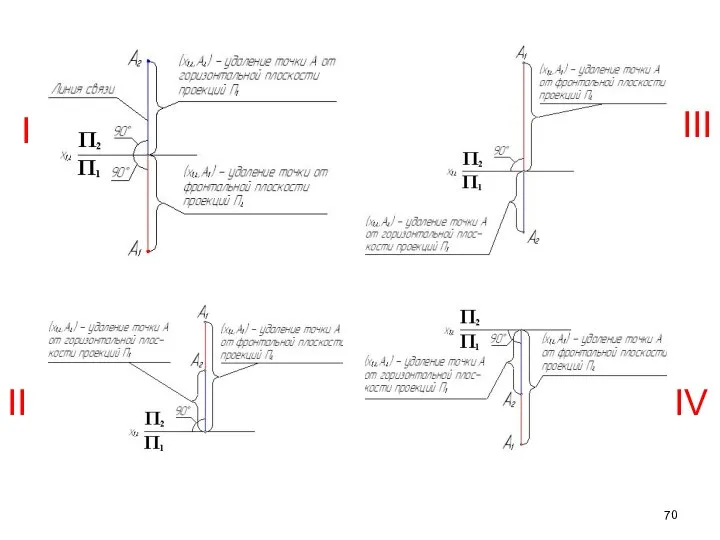
Слайд 70

I
II
III
IV

Слайд 71

Горизонтальная и фронтальная проекции точки располагаются на одной прямой, перпендикулярной

оси x1,2
А1А2 ⊥ х1,2
Расстояние от оси x1,2 до горизонтальной проекции точки определяет расстояние от самой точки до фронтальной плоскости проекций.
(х1,2 , А1) = (А, П2) - глубина
Расстояние от оси x1,2 до фронтальной проекции точки определяет расстояние от самой точки до горизонтальной плоскости проекций.
(х1,2 , А2) = (А, П1) - высота

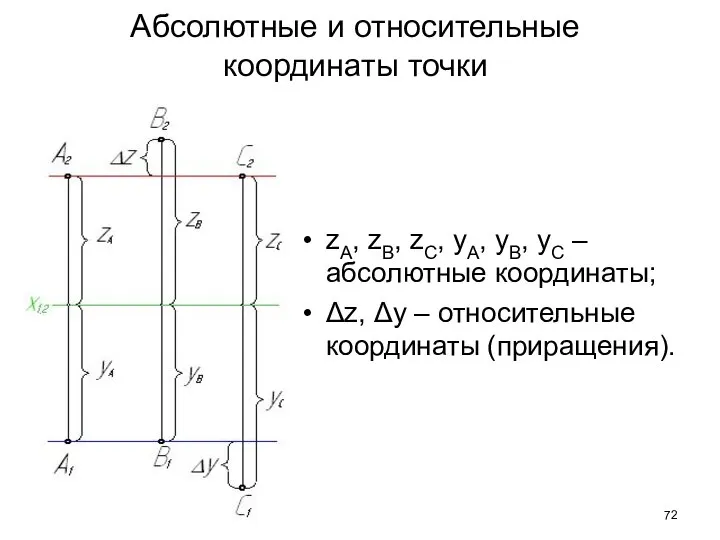
Слайд 72

Абсолютные и относительные координаты точки
zA, zB, zC, yA, yB, yC –

абсолютные координаты;
Δz, Δy – относительные координаты (приращения).

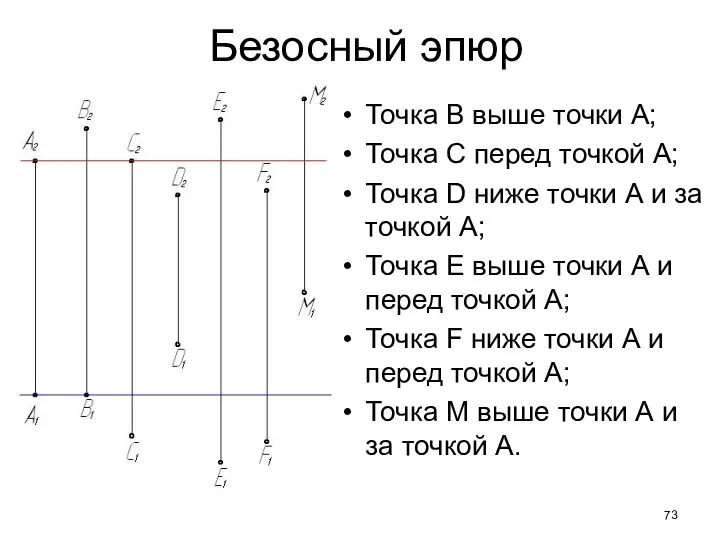
Слайд 73

Безосный эпюр
Точка В выше точки А;
Точка С перед точкой А;
Точка D

ниже точки А и за точкой А;
Точка Е выше точки А и перед точкой А;
Точка F ниже точки А и перед точкой А;
Точка М выше точки А и за точкой А.

Слайд 74

Проецирование точки в системе трех ортогональных плоскостей проекций

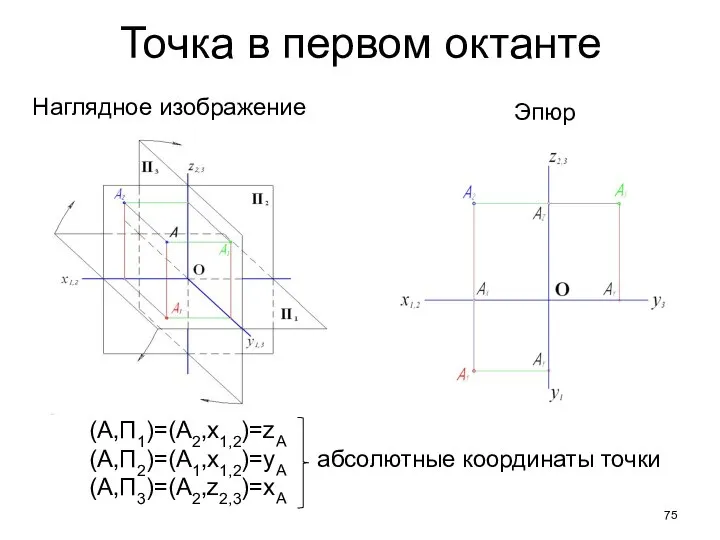
Слайд 75

Точка в первом октанте
Наглядное изображение
Эпюр
(A,П1)=(А2,х1,2)=zА
(A,П2)=(А1,х1,2)=yА абсолютные координаты точки
(A,П3)=(А2,z2,3)=хА

Слайд 76

Условия, которым должен удовлетворять эпюр точки, расположенной в любой части пространства,

в системе трех ортогональных плоскостей проекций:

А1А2 ⊥ х1,2
А2А3 ⊥ z2,3
(A1,x1,2) = (A3,z2,3)

Базовые геометрические элементы начертательной геометрии

Содержание

Чертеж – международный язык общения техников. Начертательная геометрия – грамматика этого