Лекция 1. Основы матанализа

Литература

Лобоцкая Н.Л. Основы высшей математики 2015, Москва
Ремизов А.Н. Максина А.Г.,

Определение производной

Если существует предел отношения

то функция f(x) называется дифференцируемой в точке

Геометрический смысл производной

Производная в точке x0 равна угловому коэффициенту k касательной к

Правила дифференцирования

Производные элементарных функций

Пример. Найти производную функции

.
Сначала преобразуем данную функцию:

Производная сложной функции

Если y=f(g(x)),

Дифференциал функции

Дифференциалом df(x) функции f(x) в точке х называется произведение производной

Связь между дифференциалом функции и её приращением Дифференциал функции, в общем случае

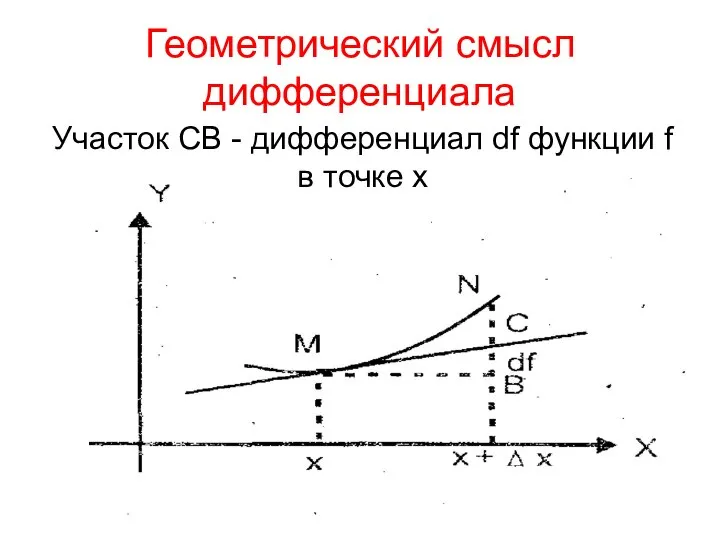
Геометрический смысл дифференциала

Участок СВ - дифференциал df функции f
в точке

Применение дифференциала для приближенных вычислений.

Оно основывается на приближённой формуле : Δf=f’(x)Δx

Применение производной при исследовании функции

Теорема о признаке возрастания и убывания функции.

Порядок действий при исследовании функции. 1. Найти область определения функции. 2.Найти производную функции

Корни этого уравнения являются экстремумами функции. 4. Найти критические точки функции,

6.По знаку производной найти интервалы возрастания и убывания функции. 7. Найти точки

3. Корни x=0, x=2 4.Эти корни стационарные и критические точки функции 5.Определим

Первообразная функция.

Функция F(x) называется первообразной функцией функции f(x) на отрезке [a,

Неопределенный интеграл.
Определение: Неопределенным интегралом функции f(x) называется вся совокупность первообразных функций

Свойства интегралов:

где u, v, w – некоторые функции от х.

Пример:

Методы интегрирования

А) Непосредственное интегрирование.

Б) Способ подстановки (замены переменных).

Сделаем замену

Пример. Найти неопределённый интеграл

В) Интегрирование по частям.

Способ основан на формуле:

Пример:

Определенный интеграл

Пусть на отрезке [ab] задана непрерывная функция y=f(x)

Найдем значения функции в этих точках и составим выражение, которое называется

Свойства определенного интеграла.

4) Если f(x) ≤ ϕ(x) на отрезке [a, b]

5) Если m и M – соответственно наименьшее и наибольшее значения

8. Для произвольных чисел a, b, c справедливо равенство:

Теорема: (Теорема Ньютона

Пример.

Дифференциальные уравнения первого порядка.
Уравнения с разделяющимися переменными
Дифференциальное уравнение первого порядка

Частным решением уравнения будет решение y= y( x ,C0 ), полученное

Делением обеих частей уравнения на произведение Q1 (y)P2 (x ) может

Пример. Дано уравнение
Найти частное решение этого уравнения, удовлетворяющее начальному условию y