Содержание
- 2. Лекцию читает к.т.н., доцент БОБРОВА ЛЮДМИЛА ВЛАДИМИРОВНА Кафедра информатики и компьютерных технологий
- 3. Рекомендуемая литература: 1. Ткаченко, Г. Г., Боброва Л.В. Математика, ч. 2. Методы оптимизации: учебно-методический комплекс. –
- 5. Пример 1 Для производства двух видов продукции фирма использует два вида ресурсов: ресурс1 – сырье, ресурс
- 6. Требуется найти план выпуска продукции, который обеспечивает максимальную выручку. Таблица 1
- 7. 1.1 Построение математической модели Обозначим: x1 – план выпуска продукции 1, x2 – план выпуска продукции
- 8. План X = (x1, x2) будет допустимым, если затраты каждого ресурса не превосходят их запасов, т.
- 9. Целевой функцией будет общая стоимость реализации плана (выручка) x1, x2: Z=40x1+100x2.
- 10. Итак, необходимо найти план выпуска продукции x1, x2, который обеспечивает максимальную выручку max Z=40 x1 +
- 11. Проверить является ли план x1=10, x2= 100 допустимым. Решение. Найдем затраты ресурсов на производство. Для выполнения
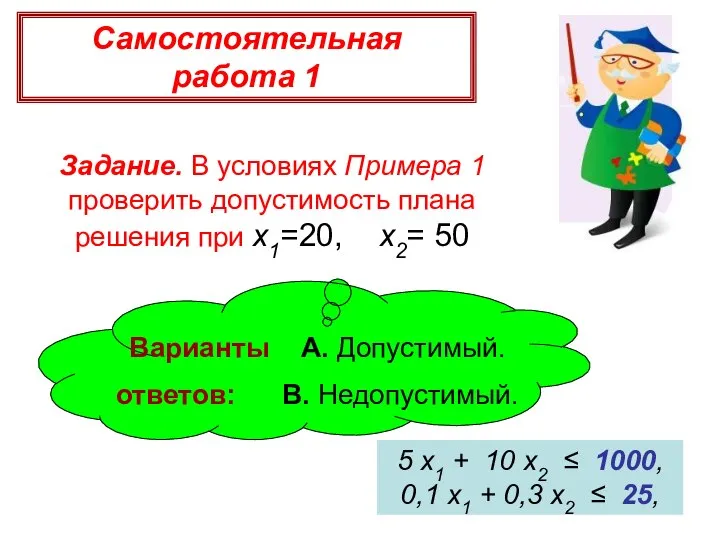
- 12. Самостоятельная работа 1 Задание. В условиях Примера 1 проверить допустимость плана решения при x1=20, x2= 50
- 13. Сверим ответы? Для выполнения этого плана потребуется 5x1+10x2 = 5⋅20 +10⋅50 = 600 кг сырья и
- 14. Решение. Выручка определяется целевой функцией Z=40x1+100x2. Значит, Z=40*10+100*100 = 10400 (у.е.). Пример 3 Для задачи Примера
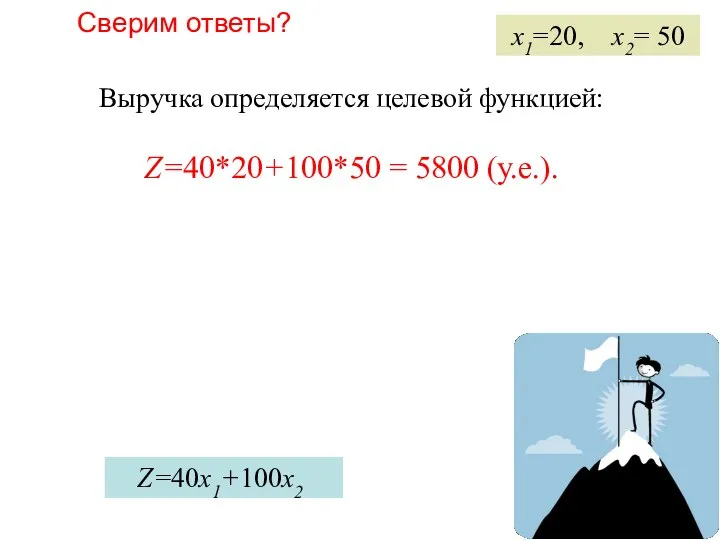
- 15. Самостоятельная работа 2 Задание. В условиях Примера 1 найти выручку от реализации плана x1=20, x2= 50
- 16. Сверим ответы? Выручка определяется целевой функцией: Z=40*20+100*50 = 5800 (у.е.). x1=20, x2= 50 Z=40x1+100x2
- 17. Пример 4 Для задачи Примера 1 найти остаток ресурсов при плане x1=50, x2= 50. 5 x1
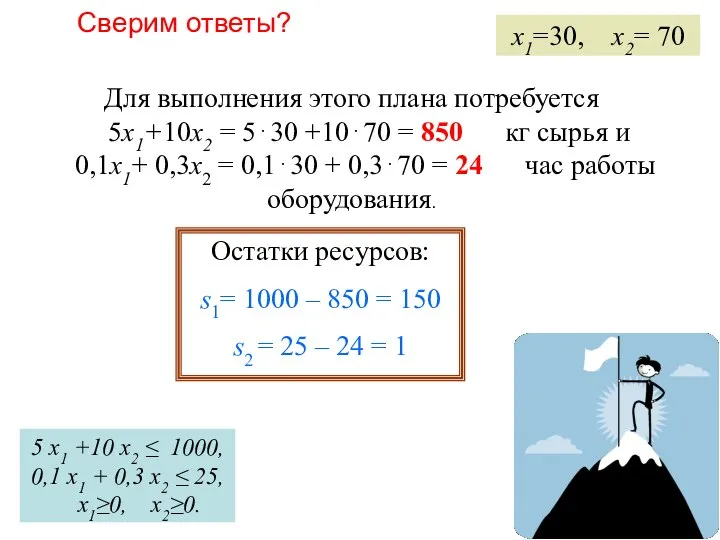
- 18. Самостоятельная работа 3 Задание. В условиях Примера 1 найти остаток ресурсов при плане x1=30, x2= 70
- 19. Сверим ответы? Для выполнения этого плана потребуется 5x1+10x2 = 5⋅30 +10⋅70 = 850 кг сырья и
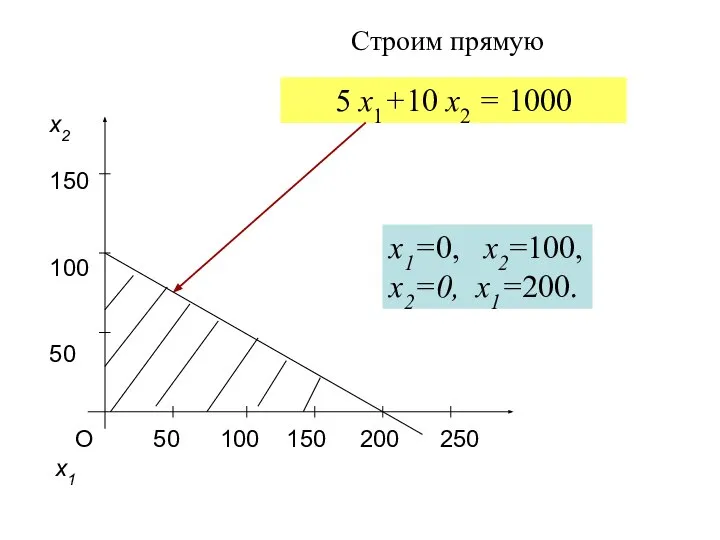
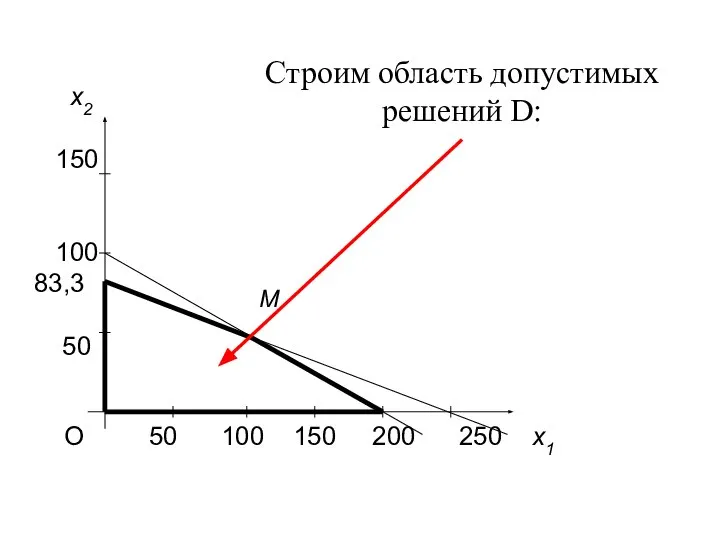
- 20. 1.2. Определение оптимального плана производства графическим методом Построим множество допустимых решений. Проведем прямые 5 x1+10 x2
- 21. О 50 100 150 200 250 x1 x2 150 100 50 x1=0, x2=100, x2=0, x1=200. 5
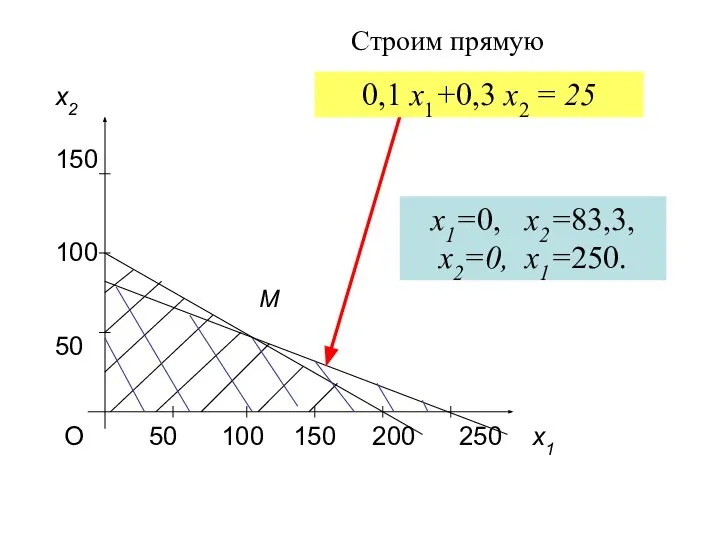
- 22. О 50 100 150 200 250 x1 x2 150 100 50 M x1=0, x2=83,3, x2=0, x1=250.
- 23. О 50 100 150 200 250 x1 x2 150 100 83,3 50 M Строим область допустимых
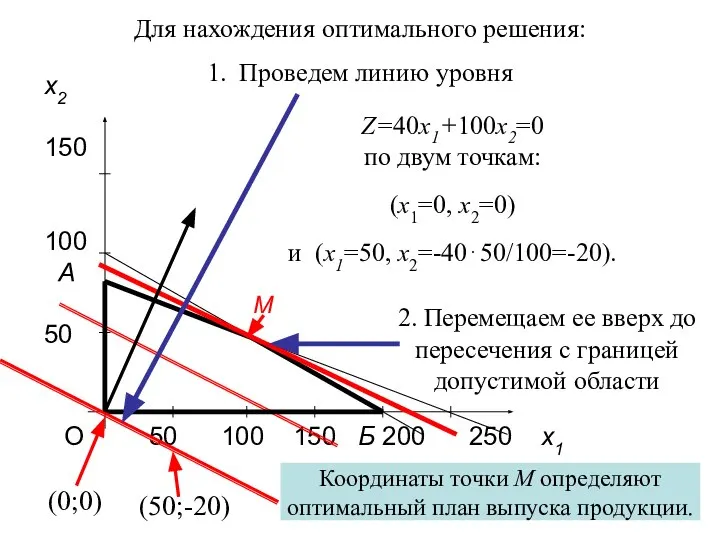
- 24. О 50 100 150 Б 200 250 x1 x2 150 100 А 50 M Z=40x1+100x2=0 по
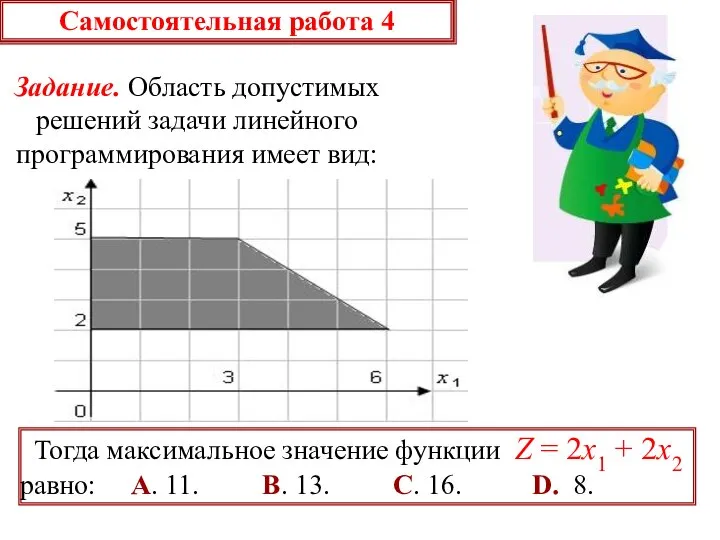
- 25. Самостоятельная работа 4 Задание. Область допустимых решений задачи линейного программирования имеет вид: Тогда максимальное значение функции
- 26. 1.3. Приведение задачи Примера 1 к канонической форме. Для этого введем две дополнительные переменные: s1 и
- 27. Ограничения (2) образуют систему двух уравнений с четырьмя неизвестными. Среди бесконечного множества решений этой системы базисные
- 28. Значения остальных переменных получаем из решения системы. Эти переменные назовем базисными. Базисное решение называется допустимым, если
- 29. 1. Пусть x1, x2 – свободные переменные. Подставляя значения x1 = 0, x2 = 0 в
- 30. Базисное решение означает, что первой и второй продукт не производятся. Это базисное решение является допустимым Выручка
- 31. 2. Пусть x1, s1 – свободные переменные. Подставляя значения x1 = 0, s1 = 0 в
- 32. Это базисное решение означает, что первый продукт не производится, второго продукта производится 100. Сырье полностью используется
- 33. 3. Пусть x1, s2 - свободные переменные. Подставляя значения x1=0, s2=0 в (2) , получаем систему
- 34. Это базисное решение означает, что первый продукт не производится, второго продукта производится 83 1/3. Сырье не
- 35. 4. Пусть x2, s1 - свободные переменные. Подставляя значения x2 = 0, s1 = 0 в
- 36. Базисное решение означает, что первого продукта производится 200, второй продукт не производится. Сырье полностью используется в
- 37. 5. Пусть x2, s2 – свободные переменные. Подставляя значения x2 = 0, s2 = 0 в
- 38. Это базисное решение означает, что первого продукта производится 250, второй продукт не производится. Не хватает для
- 39. 6. Пусть s1, s2 – свободные переменные. Тогда базисные переменные x1 и x2 найдем из системы
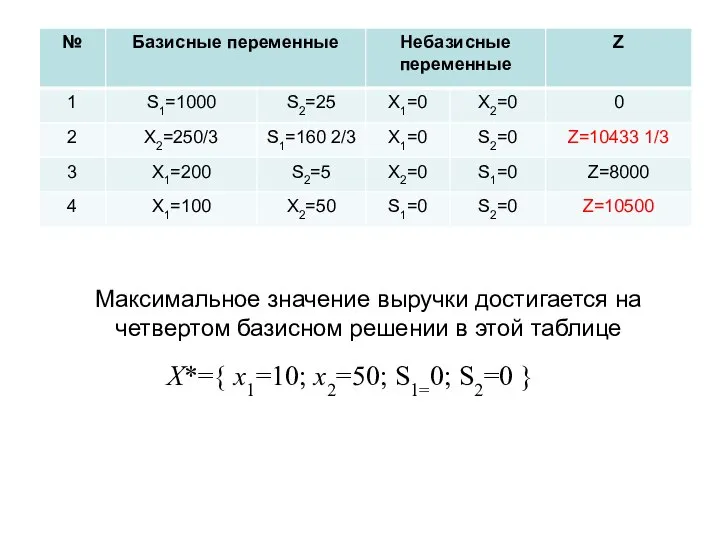
- 40. x1=100, x2=50, s1 =0, s2 =0. Это базисное решение означает, что первого продукта производится 100, второго
- 41. Максимальное значение выручки достигается на четвертом базисном решении в этой таблице X*={ x1=10; x2=50; S1=0; S2=0
- 42. 2.3. РЕШЕНИЕ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ СИМПЛЕКС-МЕТОДОМ
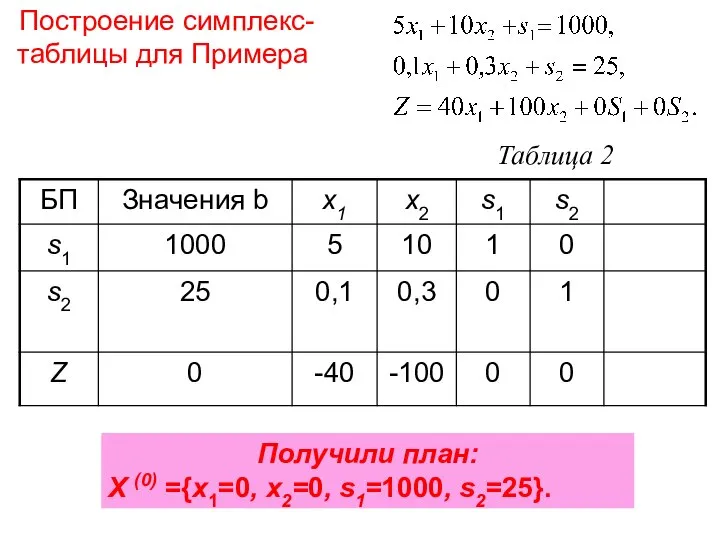
- 43. Построение симплекс-таблицы для Примера Получили план: X (0) ={x1=0, x2=0, s1=1000, s2=25}. Таблица 2
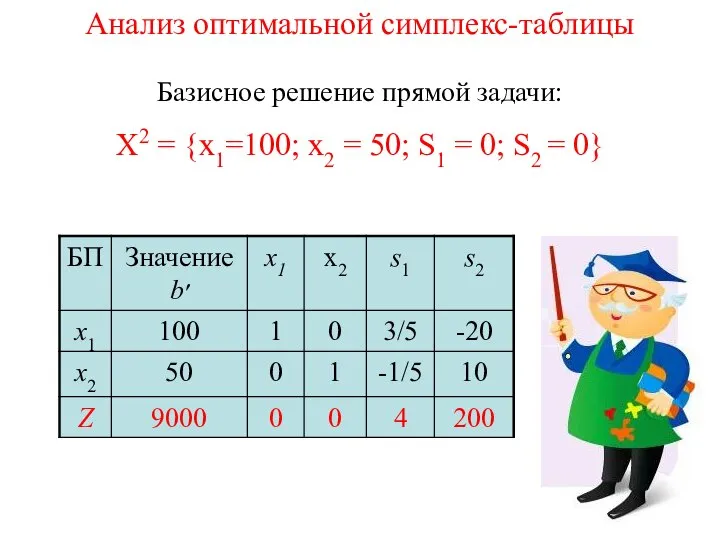
- 44. Анализ оптимальной симплекс-таблицы 1.Значения второго столбца определяют значения БП: x1 =100; x2 =50. Все переменные, не
- 45. Анализ оптимальной симплекс-таблицы Базисное решение прямой задачи: Х2 = {x1=100; x2 = 50; S1 = 0;
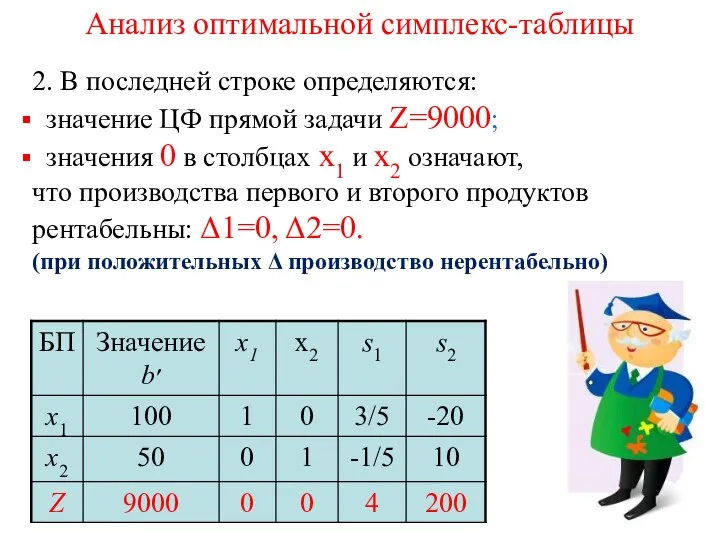
- 46. Анализ оптимальной симплекс-таблицы 2. В последней строке определяются: значение ЦФ прямой задачи Z=9000; значения 0 в
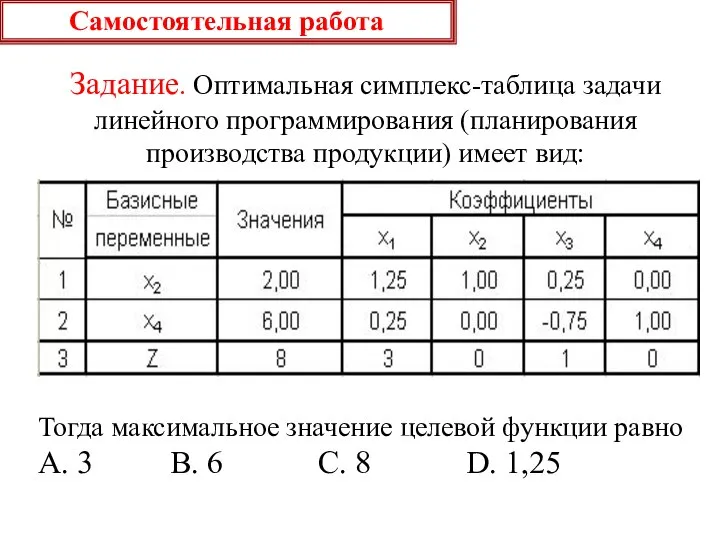
- 47. Самостоятельная работа Задание. Оптимальная симплекс-таблица задачи линейного программирования (планирования производства продукции) имеет вид: Тогда оптимальный план
- 48. Самостоятельная работа Задание. Оптимальная симплекс-таблица задачи линейного программирования (планирования производства продукции) имеет вид: Тогда максимальное значение
- 49. 1.3.3. Построение двойственной задачи линейного программирования Двойственная задача ЛП: Прямая задача 5 x1 +10 x2 =
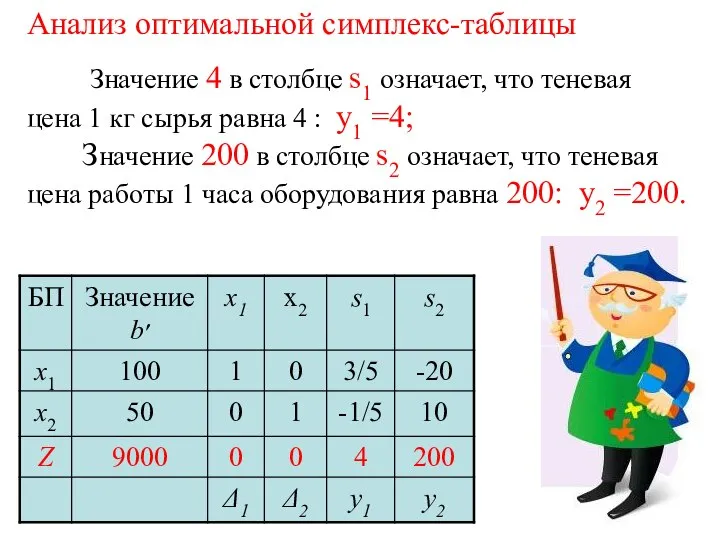
- 50. Анализ оптимальной симплекс-таблицы Значение 4 в столбце s1 означает, что теневая цена 1 кг сырья равна
- 51. 2.3. Интервалы устойчивости. После нахождения оптимального решения выполняется анализ модели на чувствительность – необходимо знать какими
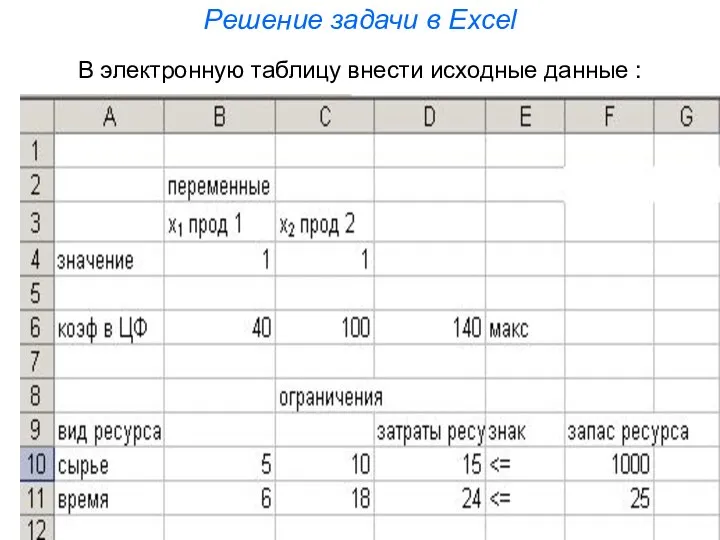
- 52. Решение задачи в Excel В электронную таблицу внести исходные данные :
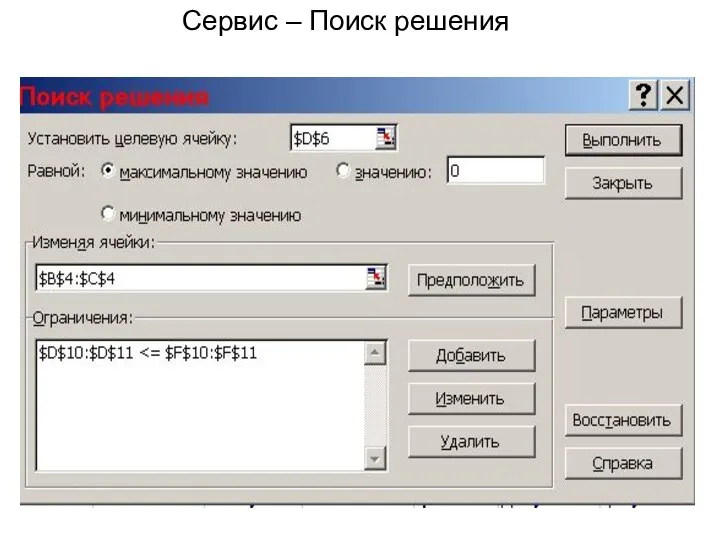
- 53. Сервис – Поиск решения
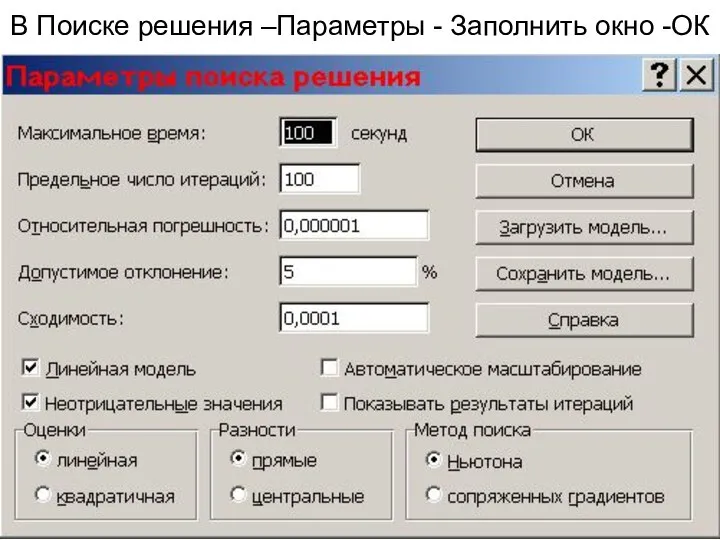
- 54. В Поиске решения –Параметры - Заполнить окно -ОК
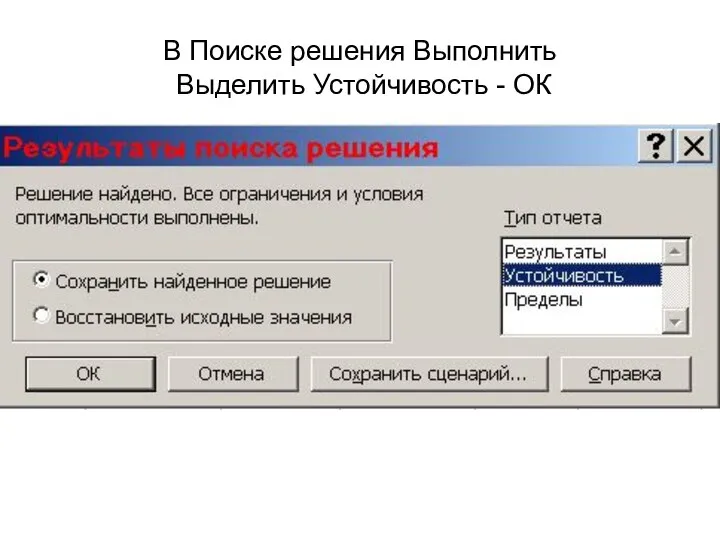
- 55. В Поиске решения Выполнить Выделить Устойчивость - ОК
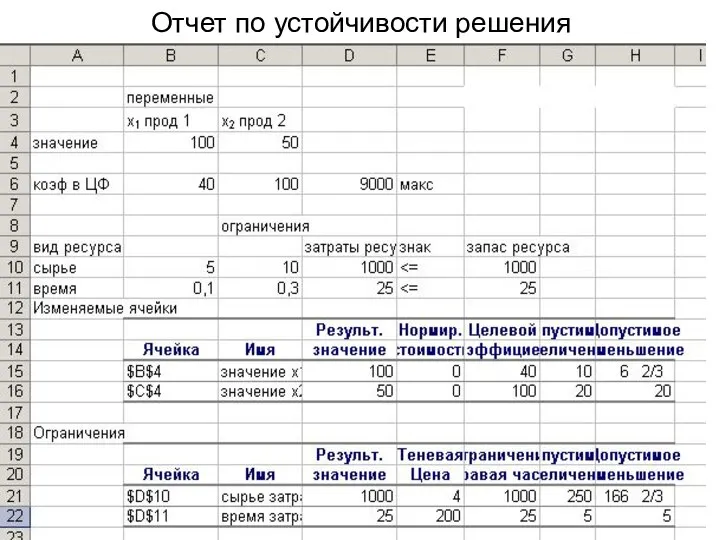
- 56. Отчет по устойчивости решения
- 58. Скачать презентацию




































 Тема: «Оказание первой медицинской помощи». учитель начальных классов ГОУ СОШ №341 г.Москва Трубицина Анна Владимировна
Тема: «Оказание первой медицинской помощи». учитель начальных классов ГОУ СОШ №341 г.Москва Трубицина Анна Владимировна Путешествие в Германию
Путешествие в Германию НАЛОГ НА ПРИБЫЛЬ ОРГАНИЗАЦИЙ
НАЛОГ НА ПРИБЫЛЬ ОРГАНИЗАЦИЙ  Индивидуальная профилактика заболеваний пародонта. Практическое освоение методов индивидуальной профилактики заболеваний п
Индивидуальная профилактика заболеваний пародонта. Практическое освоение методов индивидуальной профилактики заболеваний п Тема 4. Покупательское поведение Дисциплина «Основы маркетинга»
Тема 4. Покупательское поведение Дисциплина «Основы маркетинга»  Блок питания ПК
Блок питания ПК moi_proekty_prezentatsia_po_KG
moi_proekty_prezentatsia_po_KG Джон Бейтс Кларк (1847—1938)
Джон Бейтс Кларк (1847—1938) Как сэкономить 2 миллиарда кубометров газа в год
Как сэкономить 2 миллиарда кубометров газа в год  Красная книга Саратовской области Горностай - презентация для начальной школы_
Красная книга Саратовской области Горностай - презентация для начальной школы_ Мумтаз Махал
Мумтаз Махал Координатные телефонные станции. Устройство многократного координатного соединителя
Координатные телефонные станции. Устройство многократного координатного соединителя Классификация машинных команд
Классификация машинных команд Професійна діяльність і особистість педагога
Професійна діяльність і особистість педагога СМИ как основной институт политической коммуникации. Проблема независимости СМИ
СМИ как основной институт политической коммуникации. Проблема независимости СМИ Тема № З ТЕОРІЯ СУСПІЛЬНОГО ДОБРОБУТУ ТА СОЦІАЛЬНОЇ РИНКОВОЇ ЕКОНОМІКИ План 1. Теорія суспільного добробуту 2. Соціальна рин
Тема № З ТЕОРІЯ СУСПІЛЬНОГО ДОБРОБУТУ ТА СОЦІАЛЬНОЇ РИНКОВОЇ ЕКОНОМІКИ План 1. Теорія суспільного добробуту 2. Соціальна рин Rozważania różańcowe. Karola de Foucauld. Tajemnice chwalebne
Rozważania różańcowe. Karola de Foucauld. Tajemnice chwalebne Метод кумулятивного построении в расчете ставки дисконтирования
Метод кумулятивного построении в расчете ставки дисконтирования  Важнейшие имена и памятники эпохи Возрождения
Важнейшие имена и памятники эпохи Возрождения Игрите на баба и дядо Уча се, като играя Работа по проект – 1 клас Нина Кънева Mouse Mischief
Игрите на баба и дядо Уча се, като играя Работа по проект – 1 клас Нина Кънева Mouse Mischief Нехватка продовольствия
Нехватка продовольствия Анализ комплекса требований Закон РФ № 99-ФЗ от 4 мая 2011 года «О лицензировании отдельных видов деятельности»
Анализ комплекса требований Закон РФ № 99-ФЗ от 4 мая 2011 года «О лицензировании отдельных видов деятельности» Презентация ПОЛНОМОЧИЯ ПРЕЗИДЕНТА РФ ПО ОТНОШЕНИЮ К ОРГАНАМ ВЛАСТИ СУБЪЕКТОВ
Презентация ПОЛНОМОЧИЯ ПРЕЗИДЕНТА РФ ПО ОТНОШЕНИЮ К ОРГАНАМ ВЛАСТИ СУБЪЕКТОВ  Кратчайшие пути
Кратчайшие пути Технология процессов монтажа строительных конструкций
Технология процессов монтажа строительных конструкций Презентация по МХК ПОСТИМПРЕССИОНИЗМ
Презентация по МХК ПОСТИМПРЕССИОНИЗМ  Судебная практика. лифт. Возмещение вреда
Судебная практика. лифт. Возмещение вреда Презентация на тему "Профессия Архитектор" - скачать презентации по Педагогике
Презентация на тему "Профессия Архитектор" - скачать презентации по Педагогике