Содержание
- 2. Цели урока: Создания условий для осознанного усвоения решения тригонометрических уравнений вида a sinx + b cosx
- 3. Проверка домашнего задания sin7x – sin x =cos4x
- 4. Решение. sin7x – sin x =cos4x, 2sin3x cos4x - cos4x =0, сos4x ( 2sin3x – 1
- 5. Решить уравнение sin²x - cos²x = cos4x
- 6. Решение. sin²x-cos²x =cos4x , - (cos² - sin²x )=cos4x , -cos2x = cos²2x - sin²2x, -cos2x
- 7. Решение уравнений учащимися №628 (1) №628 (3) №629 (2)
- 8. COS X = a, где|a|≤1
- 9. x = ± arccos a + 2πn, n∈Z arccos (– a) = π - arccos a
- 10. sin X = a, где|a|≤1
- 11. x=(–1)narcsin a + πn, n ∈Z arcsin (– a) = – arcsin a
- 12. tg x = a, где a ∈ R
- 13. x = arctg a + πn, n ∈Z arctg (– a) = – arctg a
- 14. cos x = 0
- 15. x = +πn, n∈Z
- 16. cos x = 1
- 17. x = π +2πn, n∈Z
- 18. cos x = -1
- 19. x = π +2πn, n∈Z
- 20. sin x=0
- 21. x = π n, n∈Z
- 22. sin x=1
- 23. x = +2πn, n∈Z
- 24. sin x = -1
- 25. x = - +2πn, n∈Z
- 26. Решить уравнение 4sin²x – 4sinx – 3 = 0 2cos²x – sinx – 1 = 0
- 27. Ответы. 4sin²x - 4 sinx – 3 = 0 ( -1)n+1 П/6 +Пn, n Z. 2
- 28. Уравнения:
- 29. Уравнение
- 30. Уравнение . Уравнение . Поделив уравнение на , получим , , При решении этой задачи обе
- 31. Уравнение . Используя формулы sin x = 2 sin cos , cos x = cos2 -
- 32. Данное уравнение является уравнением вида , (1) где , , , которое можно решить другим способом.
- 33. Решить уравнение
- 35. Скачать презентацию








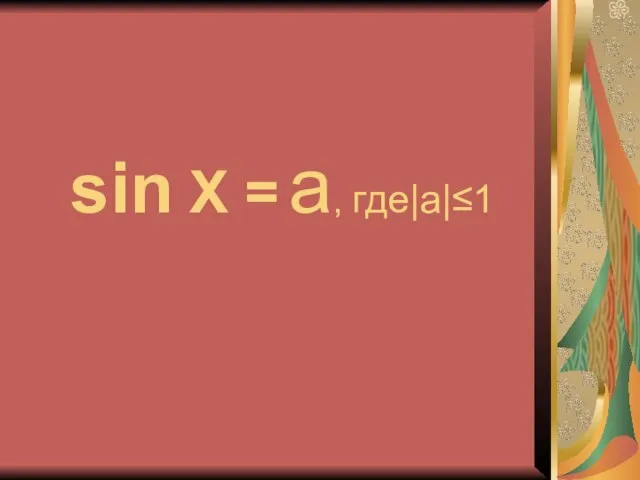

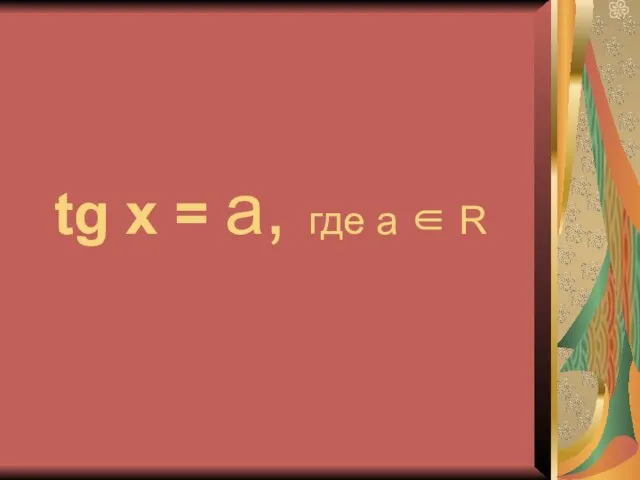


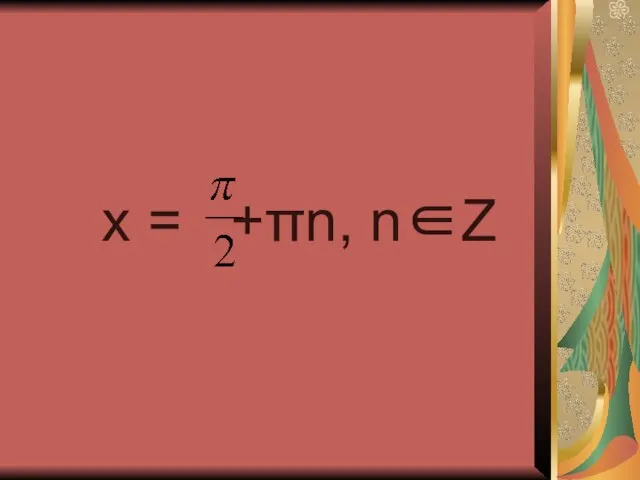

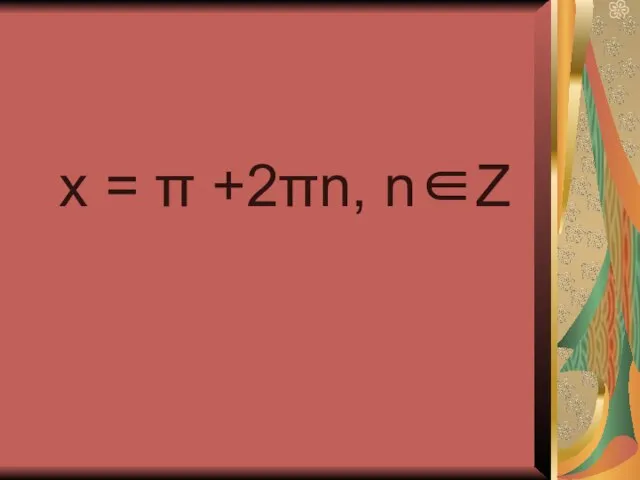
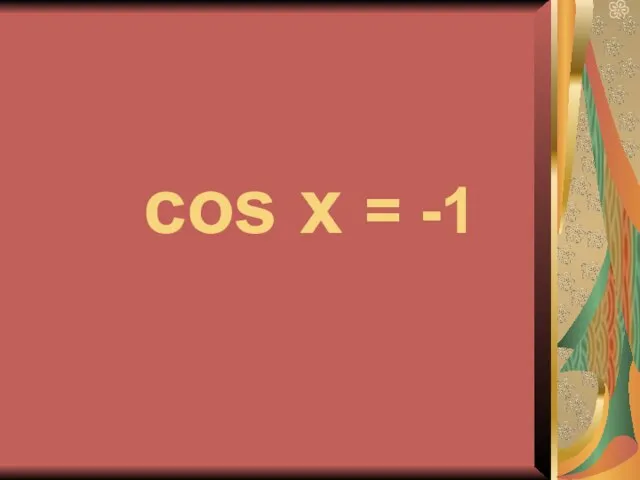
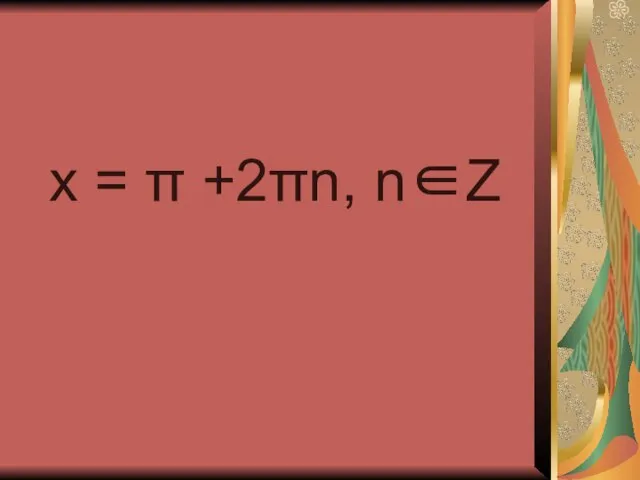
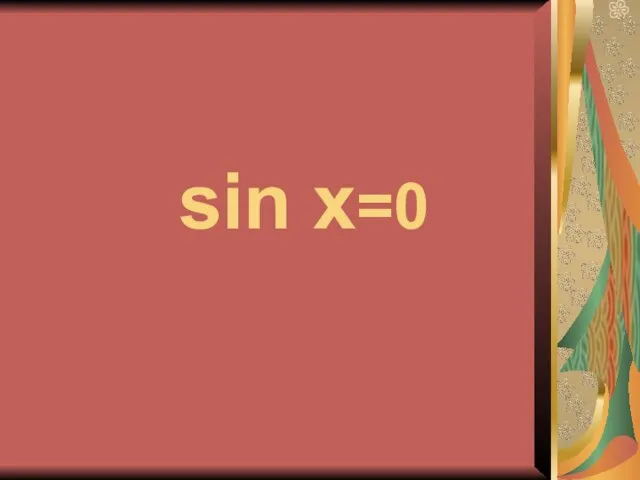
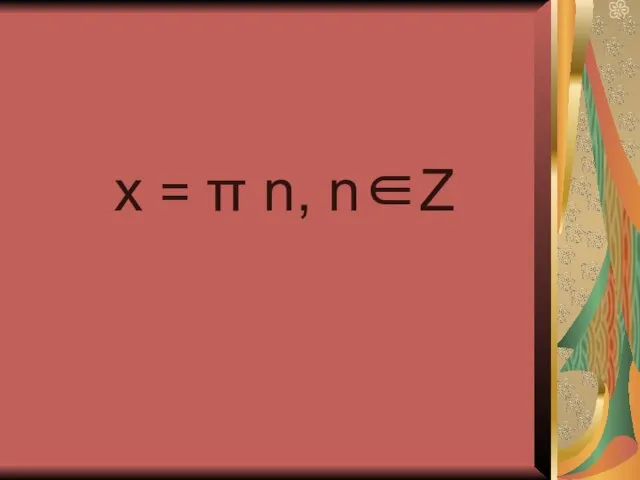
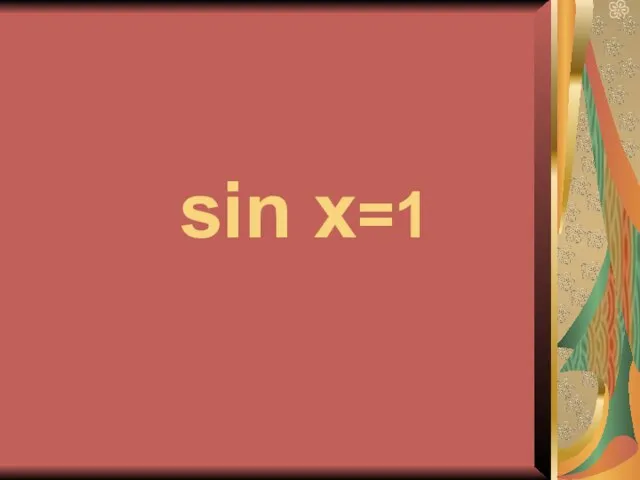
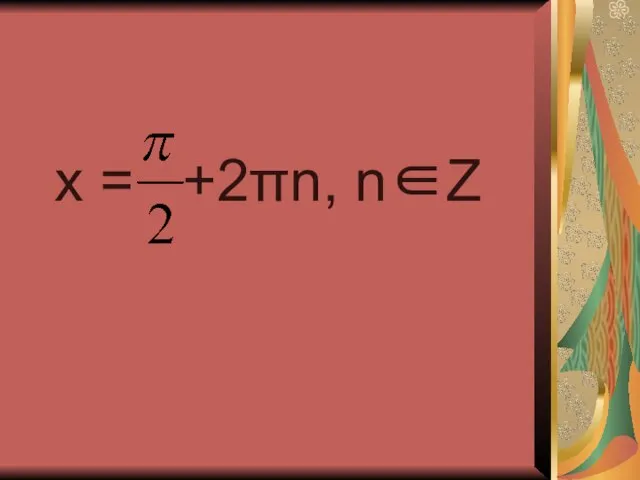
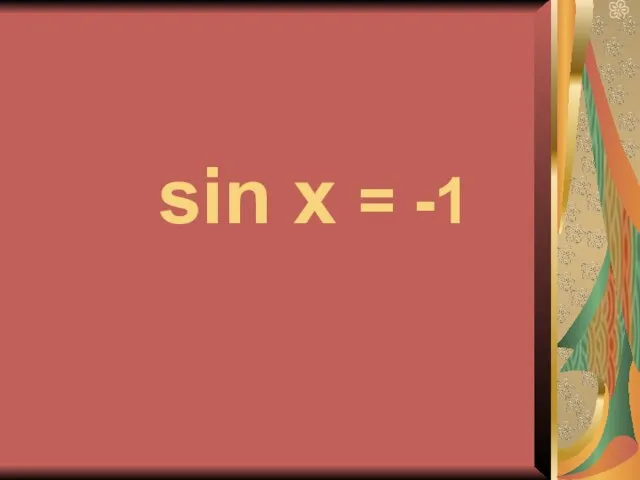
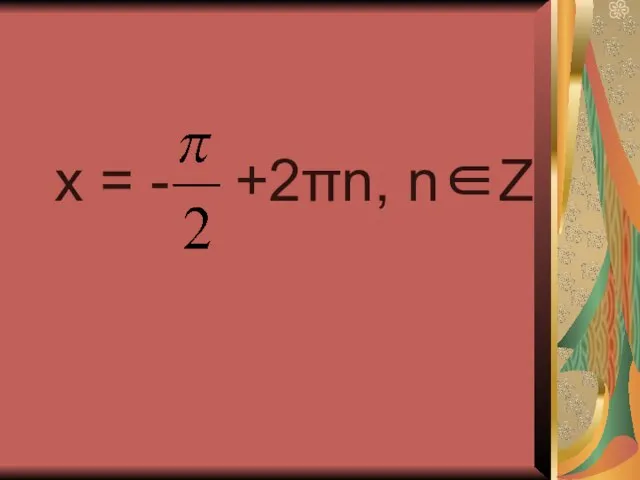








 Основные сведения о насосах
Основные сведения о насосах 01.10 Недостающая фигура
01.10 Недостающая фигура Презентация на тему "Боль в неврологии" - скачать презентации по Медицине
Презентация на тему "Боль в неврологии" - скачать презентации по Медицине Презентация Керамика
Презентация Керамика Оборотные засоби
Оборотные засоби Римская республика во 2 веке до н.э.
Римская республика во 2 веке до н.э. Викторина "Урок (час) футбола" - 2
Викторина "Урок (час) футбола" - 2 Абсолютные и относительные величины в статистике.
Абсолютные и относительные величины в статистике. Невербальные средства коммуникации
Невербальные средства коммуникации Особенности проектирования зданий для сейсмических районов
Особенности проектирования зданий для сейсмических районов . Лечение микозов
. Лечение микозов По ту сторону холста… Автор: Петрова Юлия 10 «а» класс МОУ СОШ №17
По ту сторону холста… Автор: Петрова Юлия 10 «а» класс МОУ СОШ №17  Тепловые двигатели
Тепловые двигатели Учебно-тренировочный сбор «Твоё здоровье». Правила
Учебно-тренировочный сбор «Твоё здоровье». Правила Комплексы с 5-ю 6-ю электронными лигандами
Комплексы с 5-ю 6-ю электронными лигандами  Презентация Понятие и характеристика единой системы таможенных органов РФ
Презентация Понятие и характеристика единой системы таможенных органов РФ Подготовила: Шестёро Алина
Подготовила: Шестёро Алина  Основные понятия о системе движений. Задача биомеханики двигательных действий. (Лекция 2)
Основные понятия о системе движений. Задача биомеханики двигательных действий. (Лекция 2) Технология обучения детей 9-10 лет плаванию в условиях оздоровительной группы
Технология обучения детей 9-10 лет плаванию в условиях оздоровительной группы Технологии цифрового информационного моделирования на этапе территориального планирования
Технологии цифрового информационного моделирования на этапе территориального планирования Моє хобі - футбол
Моє хобі - футбол Соціальна політика Італії
Соціальна політика Італії Решение задания В8 (ЕГЭ-2014) (анализ численного алгоритма)
Решение задания В8 (ЕГЭ-2014) (анализ численного алгоритма) Диаграмма состояний. Диаграмма, которая представляет конечный автомат
Диаграмма состояний. Диаграмма, которая представляет конечный автомат Устав Муниципального образовательного учреждения «Средняя общеобразовательная школа № 52»
Устав Муниципального образовательного учреждения «Средняя общеобразовательная школа № 52» определение расстояний до звезд
определение расстояний до звезд Moderní cukrovar HROCHŮV TÝNEC
Moderní cukrovar HROCHŮV TÝNEC babushkina_oet_316
babushkina_oet_316