Содержание
- 2. ЦЕЛИ: Повторить определение функции; основные понятия, связанные с ней; способы задания функции. Ввести понятие чётной и
- 3. ПЛАН 1.Повторение Определение функции. Способы задания функции 2.Преобразование графиков функции Симметрия относительно оси у, f(x)→ f(-
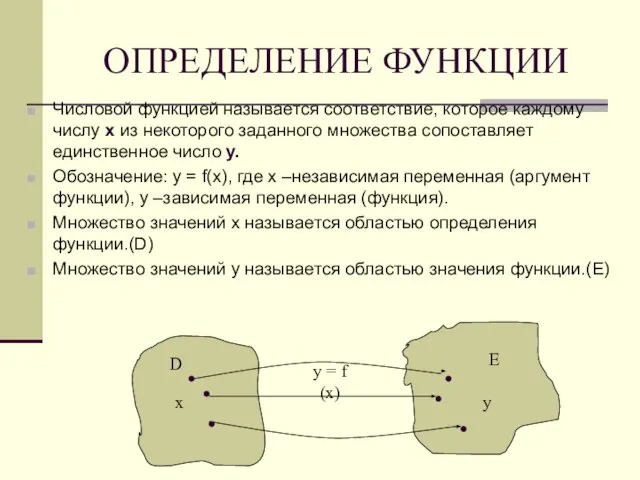
- 4. ОПРЕДЕЛЕНИЕ ФУНКЦИИ Числовой функцией называется соответствие, которое каждому числу х из некоторого заданного множества сопоставляет единственное
- 5. Пример№1 у = √х – 2 + 3 При х = 6, у(6) = √6 –
- 6. Пример №2. Найти область определения и область значения функции f (x) = 3 + 1 .
- 7. Пример №3. Найти область определения дробно-рациональной функции f (x) = 1 + 3 х + 4
- 8. Пример №4. Зависимость 2 х – 3 х2 + 1 Уже не является функцией. При х
- 9. СПОСОБЫ ЗАДАНИЯ ФУНКЦИИ Аналитический способ: функция задаётся с помощью формулы. Примеры: у = х2, у =
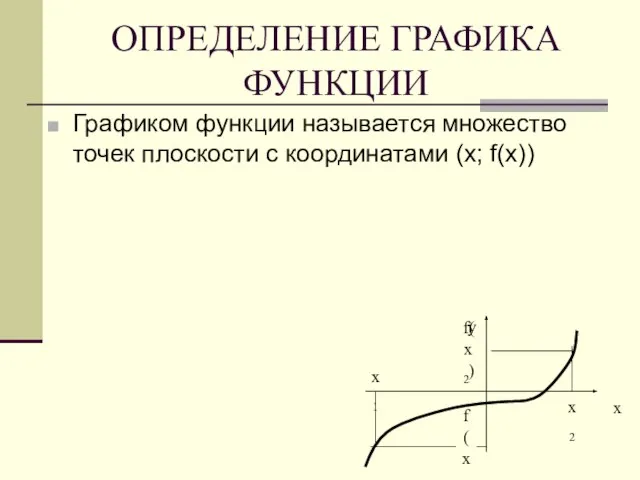
- 10. ОПРЕДЕЛЕНИЕ ГРАФИКА ФУНКЦИИ Графиком функции называется множество точек плоскости с координатами (х; f(х)) у х1 f(х1)
- 11. Пример №5. Дана функция у = 2 х – 3 |х| + 4. Принадлежит ли графику
- 12. Пример №6. Дана функция f(х) = - х2 + 6х – 8. Найдём точки пересечения графика
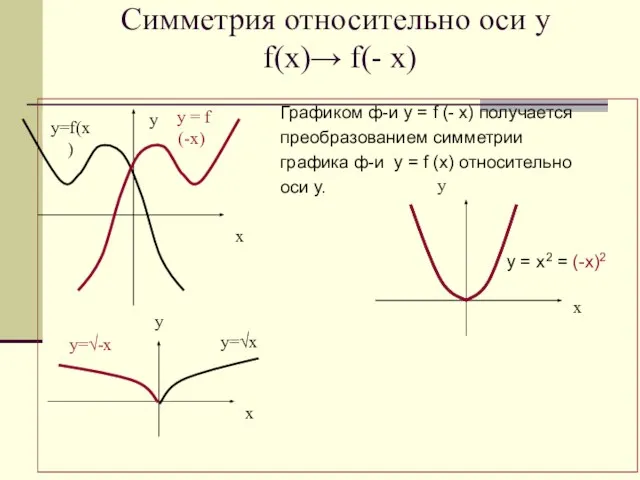
- 13. Симметрия относительно оси у f(x)→ f(- x) Графиком ф-и у = f (- х) получается преобразованием
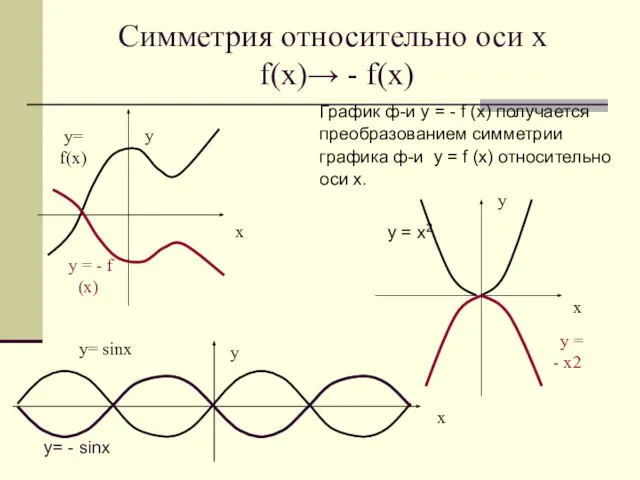
- 14. Симметрия относительно оси х f(x)→ - f(x) График ф-и у = - f (х) получается преобразованием
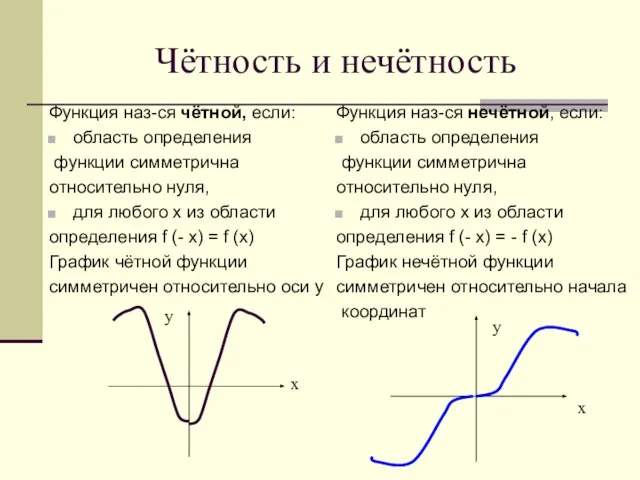
- 15. Чётность и нечётность Функция наз-ся чётной, если: область определения функции симметрична относительно нуля, для любого х
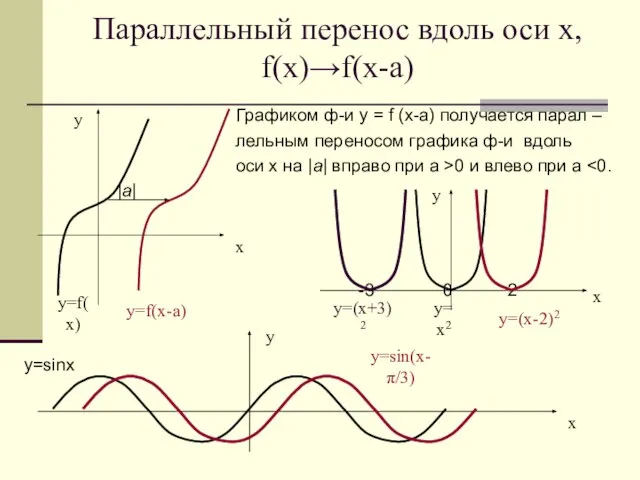
- 16. Параллельный перенос вдоль оси х, f(x)→f(x-а) Графиком ф-и у = f (х-a) получается парал – лельным
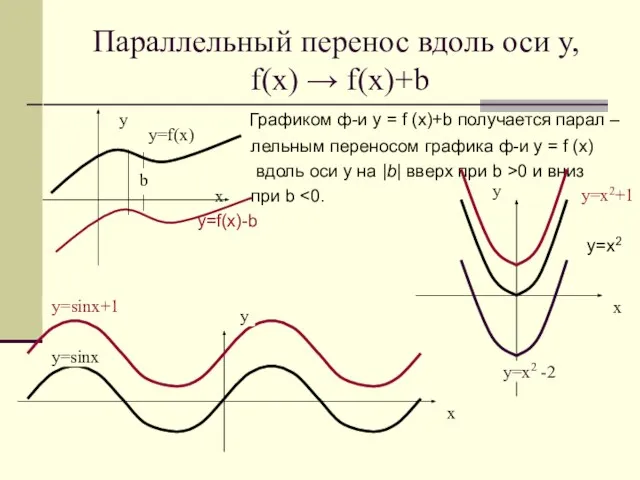
- 17. Параллельный перенос вдоль оси у, f(x) → f(x)+b Графиком ф-и у = f (х)+b получается парал
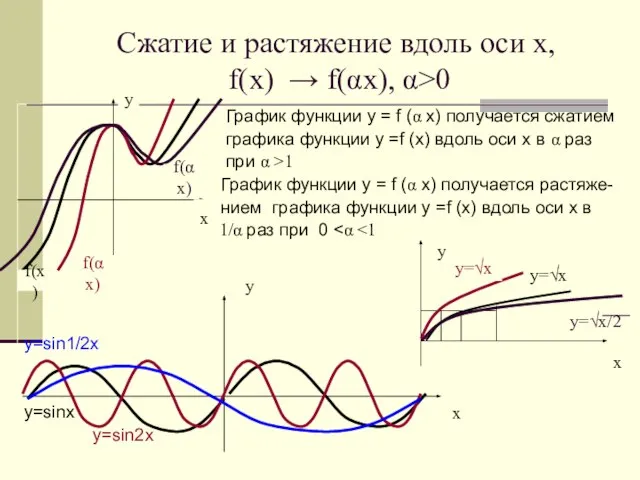
- 18. Сжатие и растяжение вдоль оси х, f(x) → f(αx), α>0 График функции у = f (α
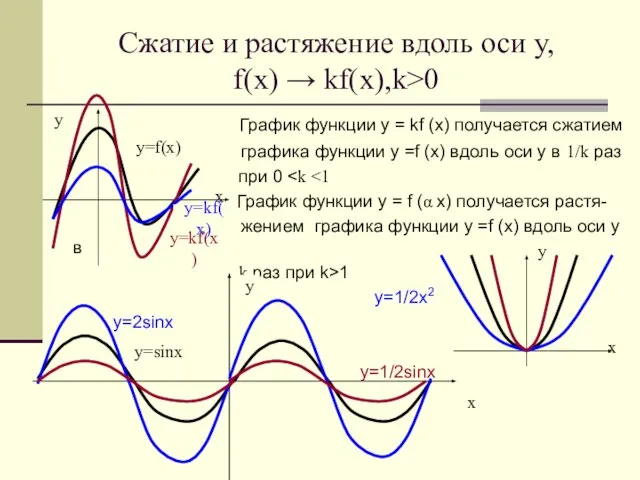
- 19. Сжатие и растяжение вдоль оси у, f(x) → kf(x),k>0 График функции у = kf (x) получается
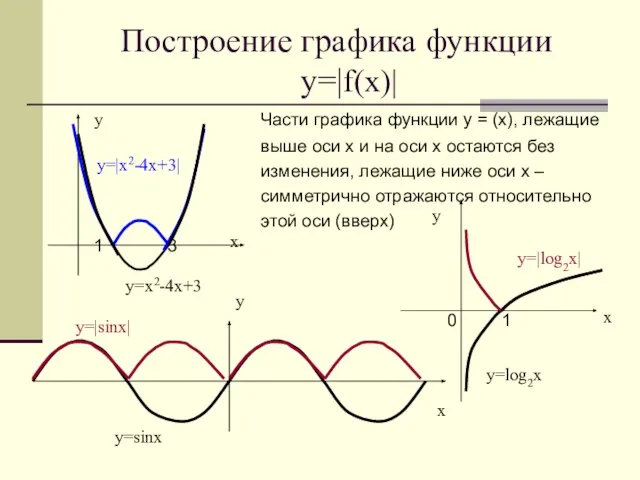
- 20. Построение графика функции у=|f(x)| Части графика функции у = (х), лежащие выше оси х и на
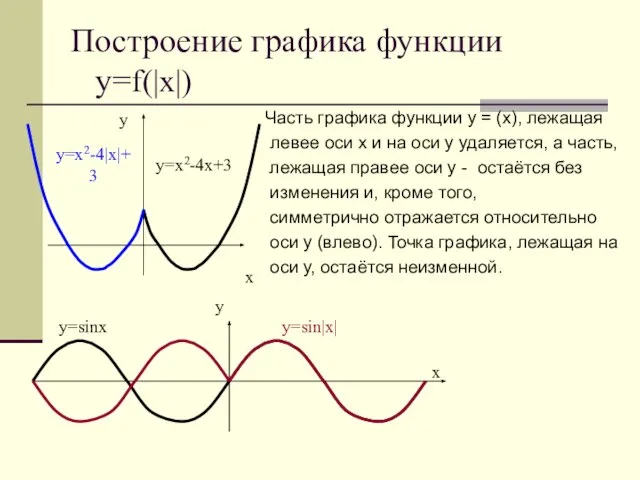
- 21. Построение графика функции у=f(|x|) Часть графика функции у = (х), лежащая левее оси х и на
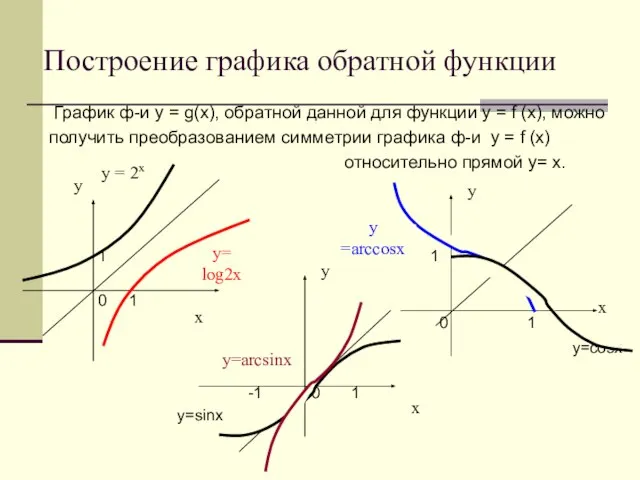
- 22. Построение графика обратной функции График ф-и у = g(х), обратной данной для функции у = f
- 24. Скачать презентацию









 Активные операции банка
Активные операции банка Тема 1.2 Світовий ринок товарів і послуг Світовий ринок товарів і послуг, його сутність та особливості формування. Теорії між
Тема 1.2 Світовий ринок товарів і послуг Світовий ринок товарів і послуг, його сутність та особливості формування. Теорії між ООП на Delphi-4. Условия в Delphi. Создание простого теста
ООП на Delphi-4. Условия в Delphi. Создание простого теста Традиции, обычаи народов мира: чепецкие татары, удмурты
Традиции, обычаи народов мира: чепецкие татары, удмурты Функции цели и задачи менеджмента
Функции цели и задачи менеджмента Презентация "Фантазийные изображения сказочных царств" - скачать презентации по МХК
Презентация "Фантазийные изображения сказочных царств" - скачать презентации по МХК Помоги принцессе
Помоги принцессе Презентация на тему "Незабудка" - скачать презентации по Педагогике
Презентация на тему "Незабудка" - скачать презентации по Педагогике ТЕМА 6. Потребительский выбор
ТЕМА 6. Потребительский выбор Монтаж плит перекрытия
Монтаж плит перекрытия Республиканская конференция «Отечественные франшизы, как фактор роста казахстанского содержания» 31.01.2012г. «КАЗАХСТА
Республиканская конференция «Отечественные франшизы, как фактор роста казахстанского содержания» 31.01.2012г. «КАЗАХСТА Наука об именах
Наука об именах Что такое натюрморт
Что такое натюрморт LifeClub. Клуб привилегий
LifeClub. Клуб привилегий Биоэнергетика мембран
Биоэнергетика мембран  История ВТ и ОС. Назначение и функции операционных систем
История ВТ и ОС. Назначение и функции операционных систем Динамика кулисного механизма
Динамика кулисного механизма Метрические задачи. Преобразования комплексного чертежа
Метрические задачи. Преобразования комплексного чертежа Историко-культурные обьекты
Историко-культурные обьекты Проектное обучение ИСТиС
Проектное обучение ИСТиС Россия
Россия  Опыт участия в программе Европейского Союза "Jean Monnet"
Опыт участия в программе Европейского Союза "Jean Monnet" Технология транспортных процессов. Транспортная логистика
Технология транспортных процессов. Транспортная логистика Логистика запасов
Логистика запасов Проведення реєстрації осіб, які виявили бажання пройти зовнішнє незалежне оцінювання в 2012 році
Проведення реєстрації осіб, які виявили бажання пройти зовнішнє незалежне оцінювання в 2012 році Презентация
Презентация Инженерные сети и оборудование зданий, техническая эксплуатация инженерных сетей зданий
Инженерные сети и оборудование зданий, техническая эксплуатация инженерных сетей зданий ДЕЛЕНИЕ ОБЫКНОВЕННЫХ ДРОБЕЙ СИНАЕВА РОЗА ИВАНОВНА МОУ «СОШ №19»
ДЕЛЕНИЕ ОБЫКНОВЕННЫХ ДРОБЕЙ СИНАЕВА РОЗА ИВАНОВНА МОУ «СОШ №19»