Содержание
- 2. Поезд движется точно на север. При наблюдении из этого поезда в момент пересечения Северного полярного круга
- 3. ϕ = +66.6°; δ = ε = +23.4°. Летнее солнцестояние Север
- 4. Распространенная ошибка: 5° Оценка: не выше 6 баллов.
- 5. Система оценивания: Угловая скорость суточного движения Солнца 8 (Не учтен cos ε) (6) Анализ вертикального движения
- 6. На Земле наступило полное лунное затмение. В ходе его наблюдений в момент начала полной фазы ученые
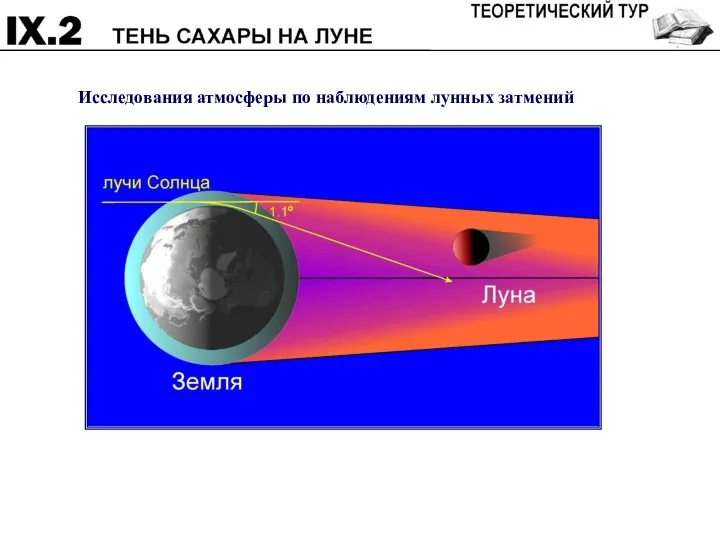
- 7. Исследования атмосферы по наблюдениям лунных затмений
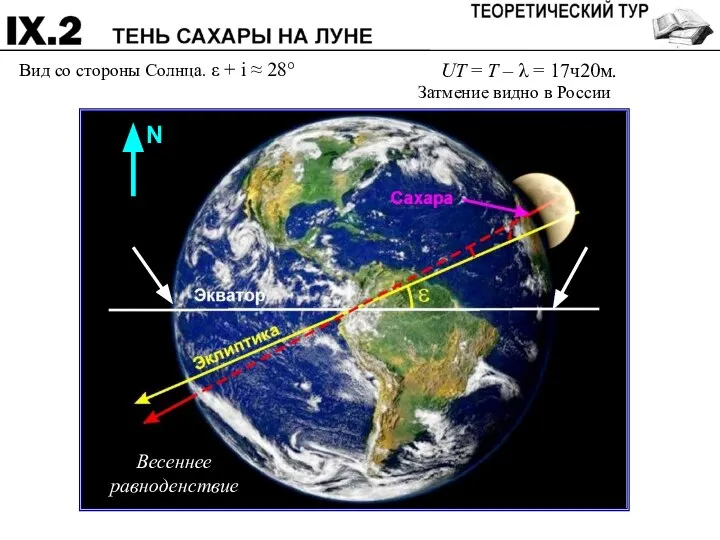
- 8. Вид со стороны Солнца. ε + i ≈ 28° UT = T – λ = 17ч20м.
- 9. Система оценивания: Весеннее равноденствие 6 (Осеннее равноденствие) (2) Заход Солнца в Сахаре 6 (Восход) (2) Всемирное
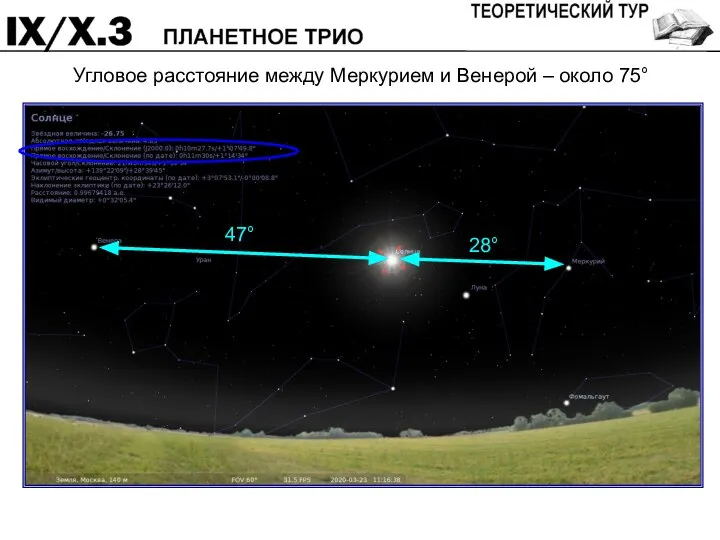
- 10. В таблице приведены экваториальные координаты Меркурия, Венеры и Марса на Земле в некоторый момент времени. Считая
- 11. Угловое расстояние между Меркурием и Венерой – около 75°
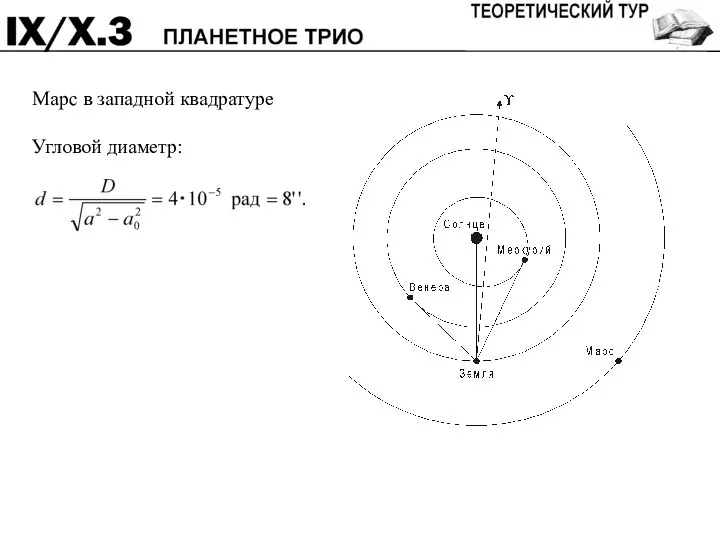
- 12. Марс в западной квадратуре Угловой диаметр:
- 13. Система оценивания: Угловое расстояние между Меркурием и Венерой 4 Противоположные элонгации 4 Положение Солнца 2 Квадратура
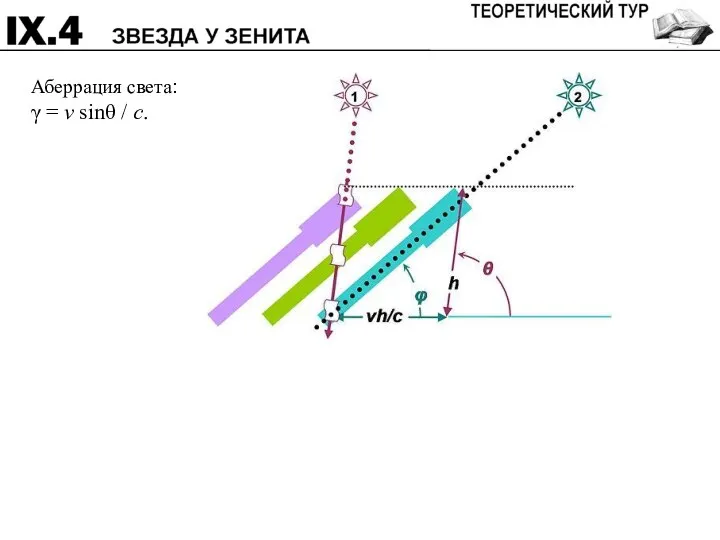
- 14. В начале XVIII века английский астроном Джеймс Бредли пытался определить параллакс звезды Этамин (γ Дракона) в
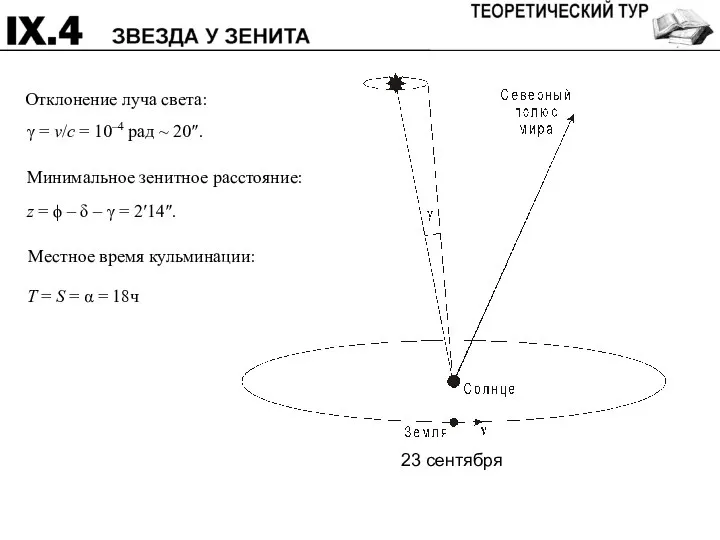
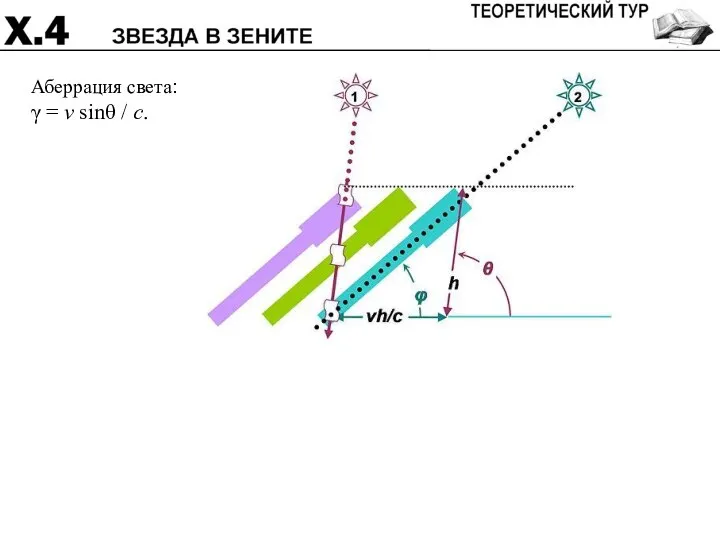
- 15. Аберрация света: γ = v sinθ / c.
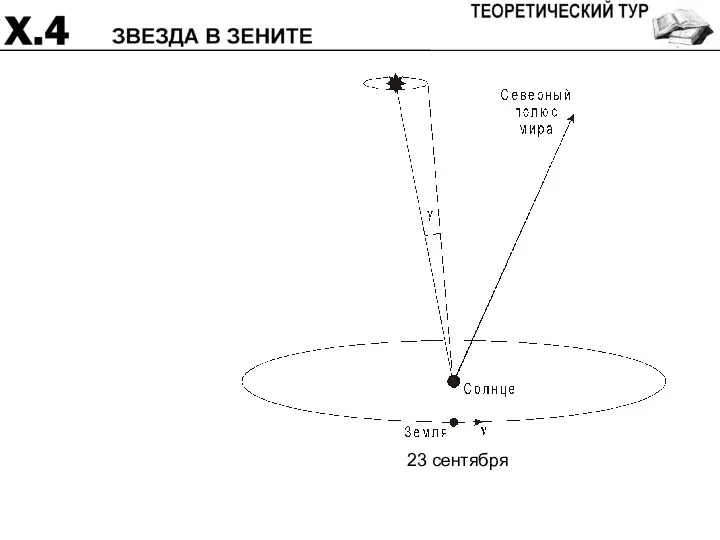
- 17. 23 сентября
- 18. Система оценивания: Направление сдвига 2 Величина сдвига 2 Сезон 4 Местное время 4 Минимальное зенитное расстояние
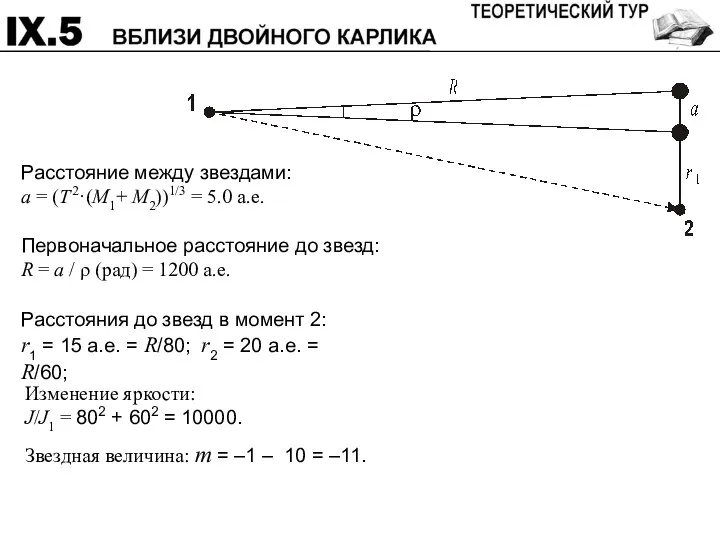
- 19. Штурман космического корабля наблюдает за двойной системой, состоящей их двух одинаковых белых карликов с массой каждого,
- 20. Расстояние между звездами: a = (T 2·(M1+ M2))1/3 = 5.0 а.е. Первоначальное расстояние до звезд: R
- 21. Система оценивания: Расстояние между звездами 4 (Одинарная масса) (0) Расстояние до звезд в первый момент 2
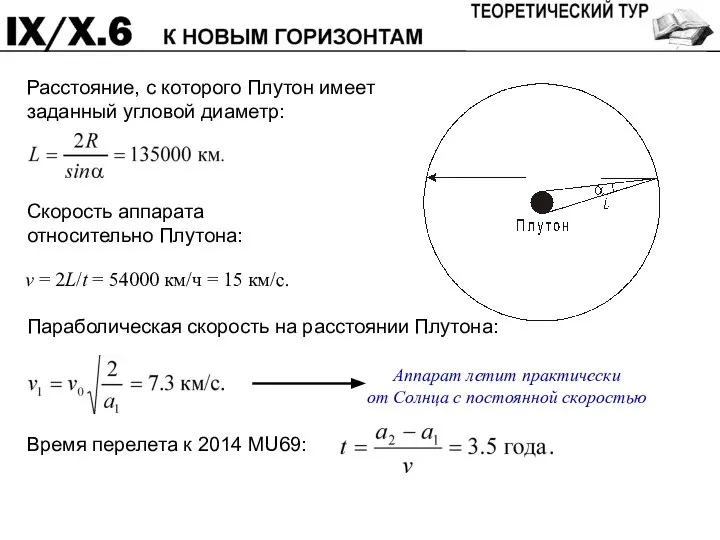
- 22. Когда межпланетная станция New Horizons пролетала около Плутона (радиус 1190 км) на расстоянии 33 а.е. от
- 24. Система оценивания: Расстояние, соответствующее 1° 4 Скорость аппарата относительно Плутона 4 (Ошибка в 2 раза) (0)
- 25. Океанский корабль движется в сторону севера, пересекая параллель +60° с.ш. Капитан корабля держит курс точно на
- 26. Отклонение азимута: A0 = ρ/cosϕ = 80′.
- 27. Максимальная поперечная скорость: vP = v sin A0 = 0.70 км/ч.
- 28. Система оценивания: Отклонение азимута 6 (40’) (0) Поперечная компонента скорости 4 Максимальное отклонение от курса 6
- 29. На стационарной лунной обсерватории будущего проводится изучение атмосферы Земли на основе спектроскопии звезд у земного лимба.
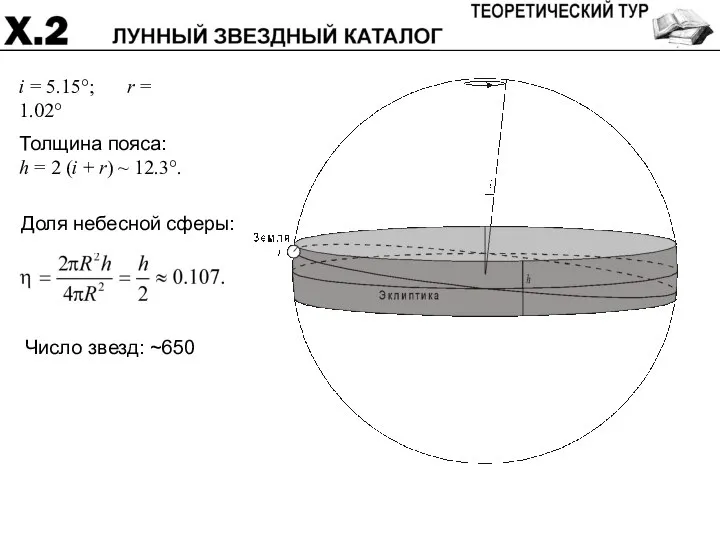
- 30. i = 5.15°; r = 1.02° Толщина пояса: h = 2 (i + r) ~ 12.3°.
- 31. Система оценивания: Факторы, влияющие на ширину области 10 (Прецессия орбиты Луны) (6) (Видимые размеры Земли) (4)
- 32. В какой сезон и в какое местное (среднее солнечное) время звезда Грумиум (ξ Дракона) может оказаться
- 33. Аберрация света: γ = v sinθ / c.
- 35. 23 сентября
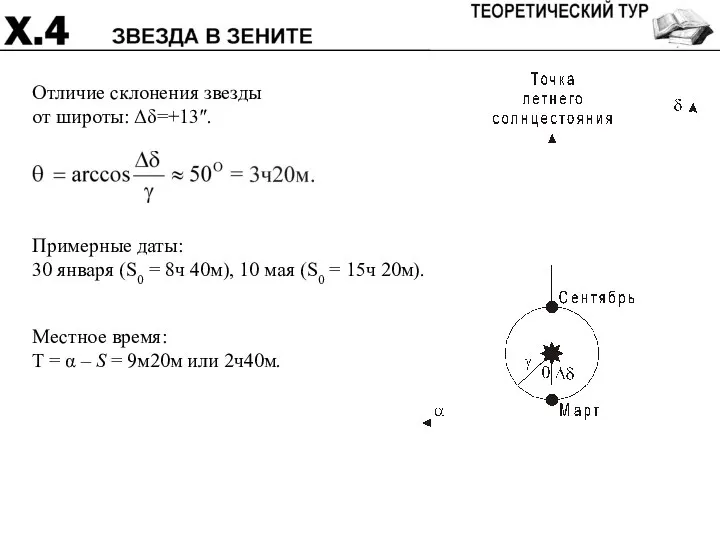
- 36. Отличие склонения звезды от широты: Δδ=+13″. Примерные даты: 30 января (S0 = 8ч 40м), 10 мая
- 37. Система оценивания: Указание аберрации света 2 Величина сдвига 2 Направление сдвига 4 Сезон 4 (2+2) Местное
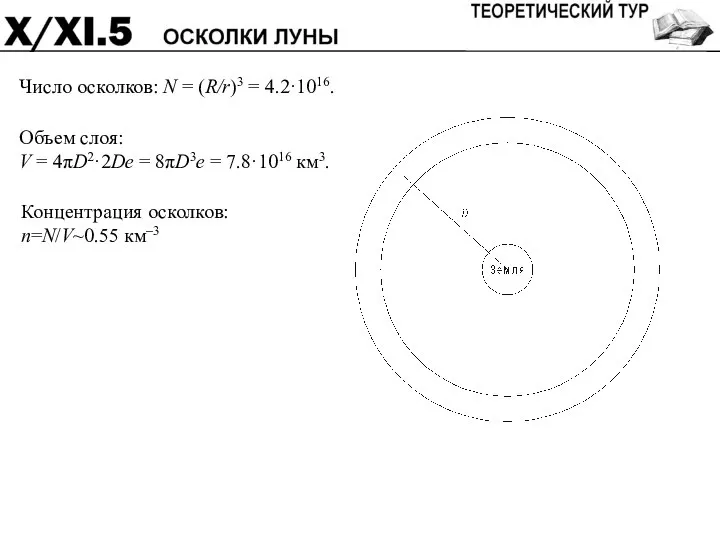
- 38. Враждебные инопланетяне разрушили Луну, превратив ее в огромное количество шарообразных осколков диаметром 10 м. Все эти
- 39. Число осколков: N = (R/r)3 = 4.2·1016. Объем слоя: V = 4πD2·2De = 8πD3e = 7.8·1016
- 40. Яркость одного осколка: j = Jr2/R2 (J – яркость Луны в первой четверти) Суммарная яркость (N/2)
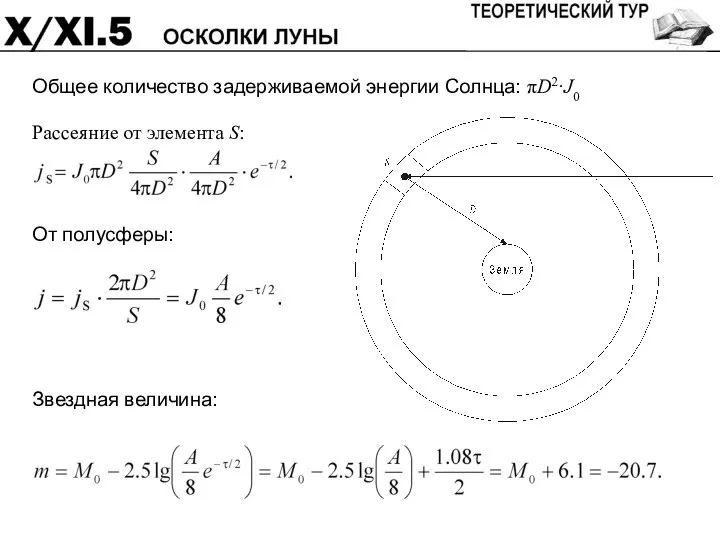
- 41. Общее количество задерживаемой энергии Солнца: πD2·J0
- 42. Система оценивания: Концентрация осколков 4 Затенение осколков 2 Модель определения звездной величины 6 Расчет звездной величины
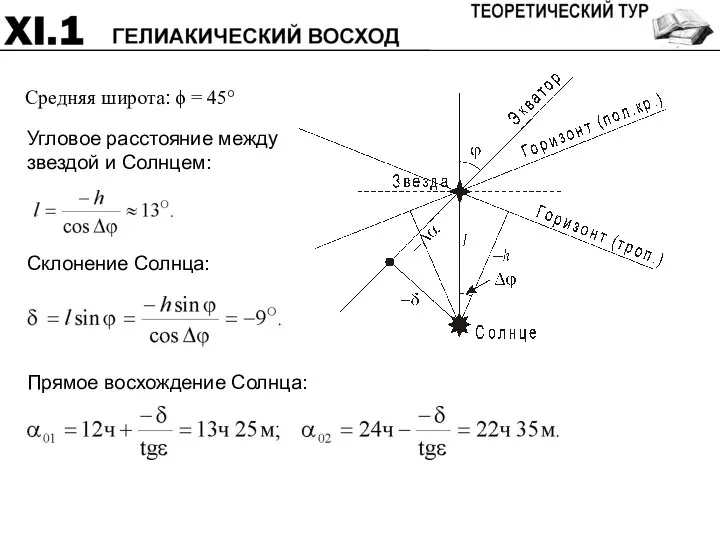
- 43. Гелиакическим восходом звезды называется ее восход на фоне утренней зари, при котором она впервые становится видимой
- 44. Средняя широта: ϕ = 45°
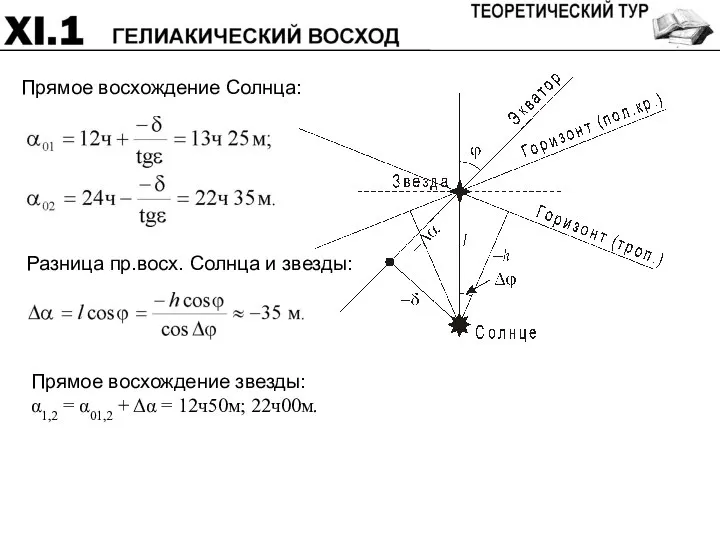
- 45. Прямое восхождение Солнца: Прямое восхождение звезды: α1,2 = α01,2 + Δα = 12ч50м; 22ч00м.
- 46. Система оценивания: Представление о расположении Солнца и звезды 4 Склонение Солнца 2 Прямое восхождение Солнца 4
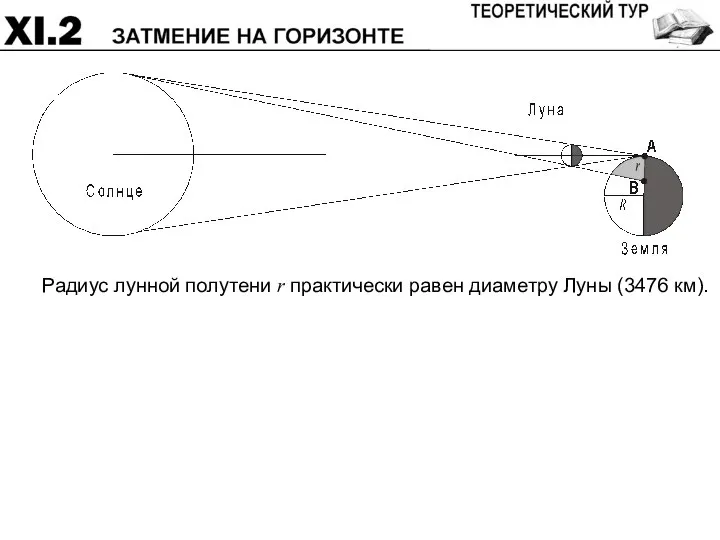
- 47. В некоторый момент времени в пункте A на Земле наблюдается полное солнечное затмение с фазой 1.000,
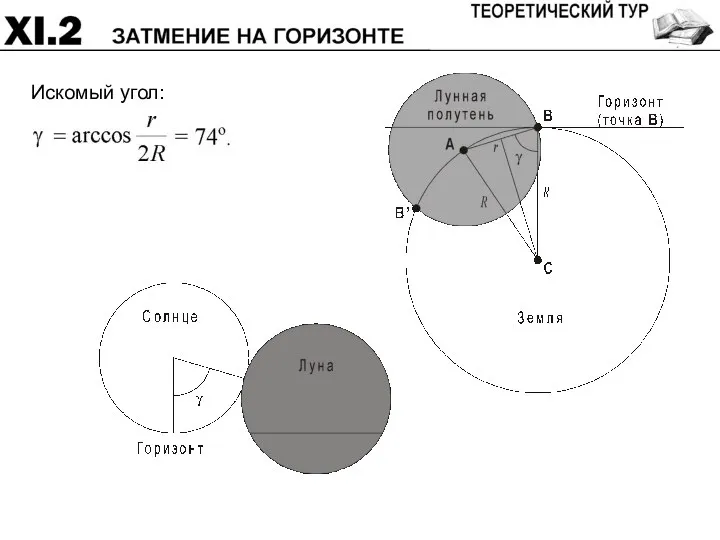
- 48. Радиус лунной полутени r практически равен диаметру Луны (3476 км).
- 50. 3 октября 1986 г.
- 51. Система оценивания: Положение тени и полутени на Земле 4 Вывод об угле γ 4 Размер полутени
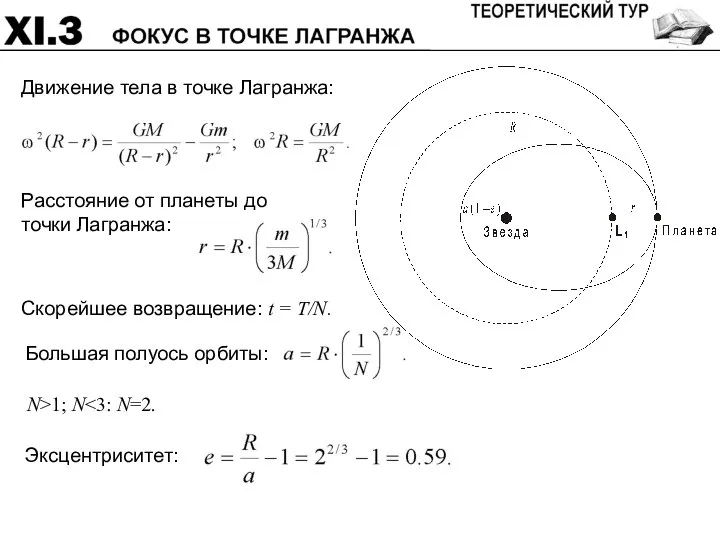
- 52. Планета обращается вокруг звезды с массой M по круговой орбите с радиусом R. С нее стартует
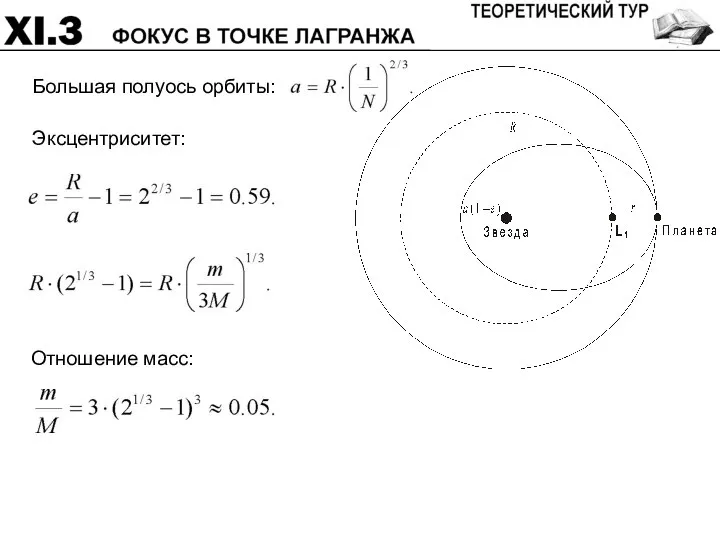
- 53. Движение тела в точке Лагранжа: Скорейшее возвращение: t = T/N. N>1; N
- 54. Эксцентриситет:
- 55. Система оценивания: Расстояние между планетой и точкой Лагранжа 6 Условие скорейшего возвращения 4 Отношение масс 6
- 56. Суть известного эффекта Пойнтинга-Робертсона состоит в тормозящем действии боковых солнечных фотонов, имеющих встречную компоненту скорости относительно
- 57. Эффективная масса Солнца: M’=0.92M.
- 58. Полная энергия частицы:
- 59. Система оценивания: Сравнение сил гравитации и св.давления 2 (либо вычисление эффективной массы Солнца) Выражение для силы
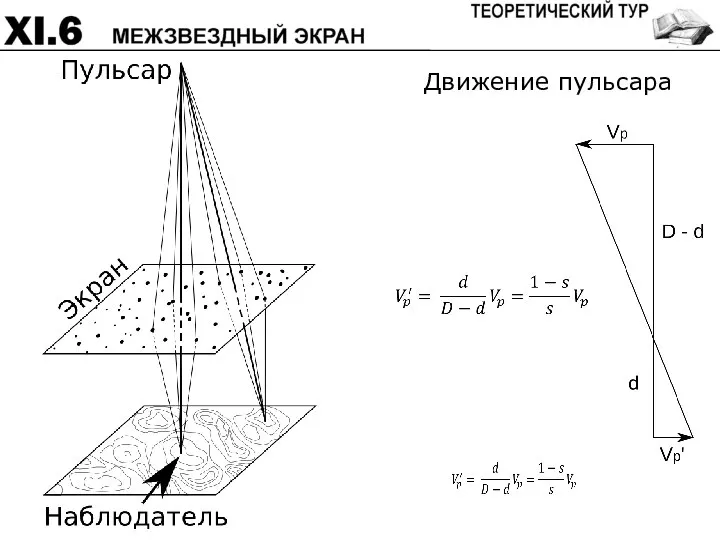
- 60. Излучение пульсара на пути к Земле проходит через тонкий рассеивающий слой (экран), расположенный на расстоянии двух
- 61. Движение пульсара
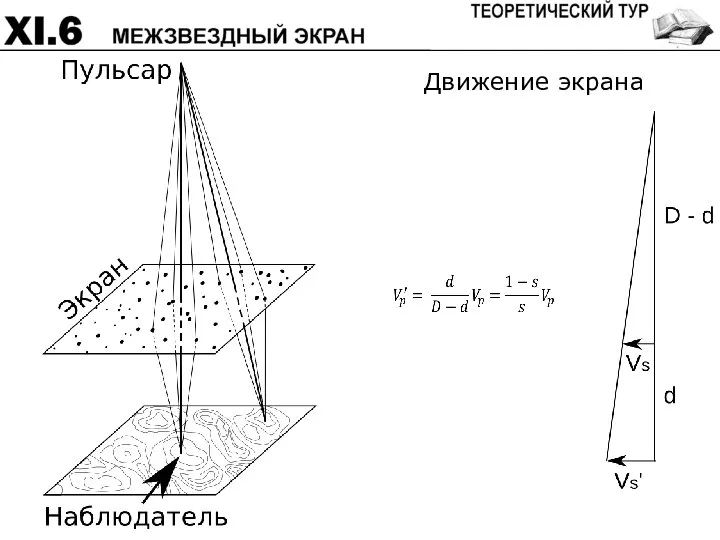
- 62. Движение экрана
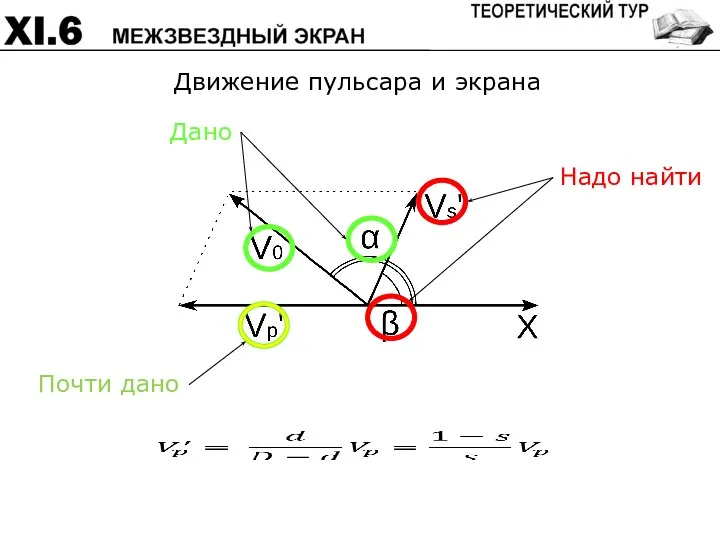
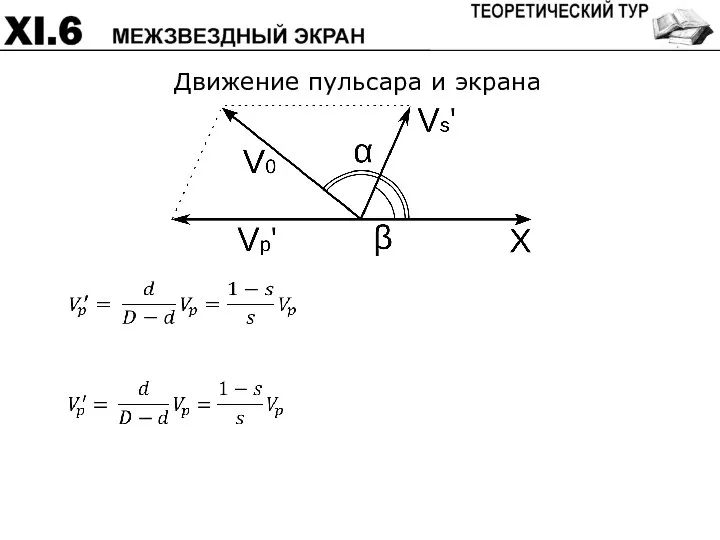
- 63. Движение пульсара и экрана Дано Надо найти Почти дано
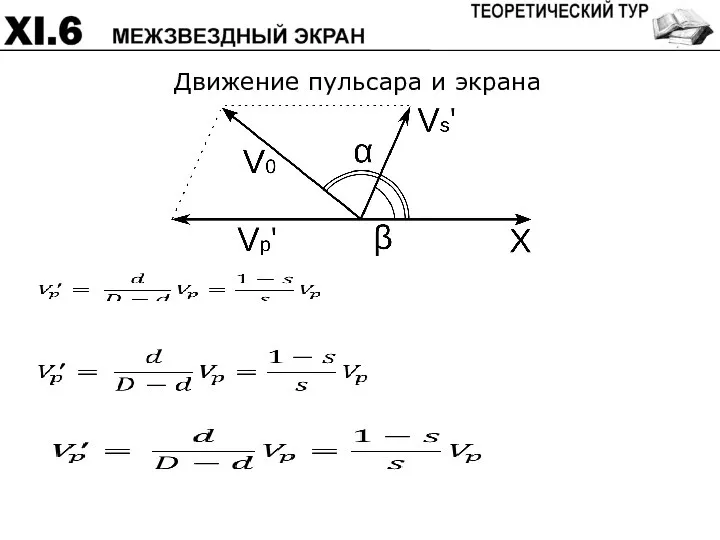
- 64. Движение пульсара и экрана
- 65. Движение пульсара и экрана
- 67. Скачать презентацию







































 12 апреля - - День Космонавтики - презентация по Астрономии скачать бесплатно
12 апреля - - День Космонавтики - презентация по Астрономии скачать бесплатно Мы во Вселенной
Мы во Вселенной Знания о космосе и космонавтах!
Знания о космосе и космонавтах! Звездное небо
Звездное небо  Метеороиды и природа кратеров на луне и других телах солнечной системы
Метеороиды и природа кратеров на луне и других телах солнечной системы Небесные координаты. Звездные карты
Небесные координаты. Звездные карты Наша галактика. Зоряні скупчення та їх асоціації. Туманності. Підсистеми галактики та її спіральні структури
Наша галактика. Зоряні скупчення та їх асоціації. Туманності. Підсистеми галактики та її спіральні структури Космические послания
Космические послания Солнце - ближайшая звезда
Солнце - ближайшая звезда Что такое кометы? - презентация по Астрономии скачать
Что такое кометы? - презентация по Астрономии скачать  Малые тела Солнечной системы (астероиды, карликовые планеты и кометы)
Малые тела Солнечной системы (астероиды, карликовые планеты и кометы) Движение и фазы Луны. Затмения Солнца и Луны
Движение и фазы Луны. Затмения Солнца и Луны Астрономия, как наука. Вселенная
Астрономия, как наука. Вселенная Введение в курс. Окружающий космос
Введение в курс. Окружающий космос Планета Венера
Планета Венера В космосе - презентация по Астрономии скачать бесплатно
В космосе - презентация по Астрономии скачать бесплатно Комета Галлея
Комета Галлея Своя игра, посвященная Дню Космонавтики
Своя игра, посвященная Дню Космонавтики Спутник Земли. Луна - презентация по Астрономии скачать
Спутник Земли. Луна - презентация по Астрономии скачать  Законы Кеплера
Законы Кеплера Пригоди Шустрика та Бистрика. 5 клас
Пригоди Шустрика та Бистрика. 5 клас Квазары. Образование галактик
Квазары. Образование галактик Астрономія та астрологія. Значення астрономії для формування світогляду людини
Астрономія та астрологія. Значення астрономії для формування світогляду людини Загустайская средняя общеобразовательная школа Основы молекулярной физики. Исполнитель: ученица10 класса Сор
Загустайская средняя общеобразовательная школа Основы молекулярной физики. Исполнитель: ученица10 класса Сор Через тернии – к звёздам… Астрономия на координатной плоскости
Через тернии – к звёздам… Астрономия на координатной плоскости Созвездие - Телец
Созвездие - Телец Черные дыры
Черные дыры Проведение экспериментов с животными, для подготовки в последующих полетах человека в космос
Проведение экспериментов с животными, для подготовки в последующих полетах человека в космос