Содержание
- 2. Общие положения Методы преобразования плоскостей проекций применяются для облегчения решения какой-либо поставленной задачи. В пространстве с
- 3. Общие положения Все методы можно разделить на две группы: 1) Объект жестко зафиксирован в пространстве. Вокруг
- 4. Общие положения Независимо от метода преобразования, в задаче выделяется главный элемент, с которым и выполняются преобразования.
- 5. Общие положения Типовые задачи: Главный элемент – прямая Прямую общего положения преобразовать в линию уровня L→
- 6. Общие положения Главный элемент – плоскость 3) Плоскость общего положения преобразовать в проецирующую α→ α‘ ┴
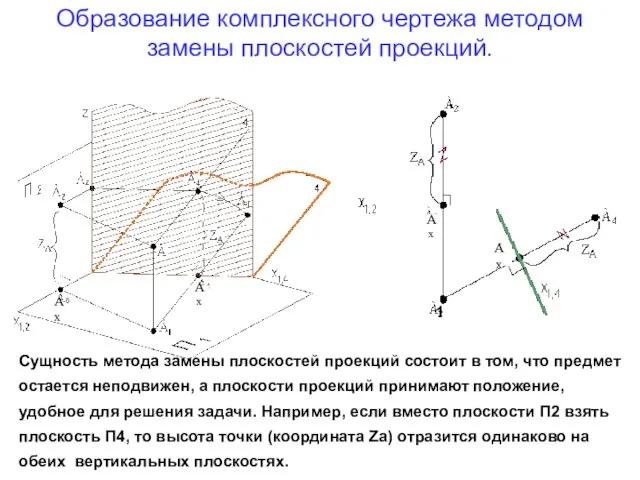
- 7. Образование комплексного чертежа методом замены плоскостей проекций. Ах Ах Ах Ах Сущность метода замены плоскостей проекций
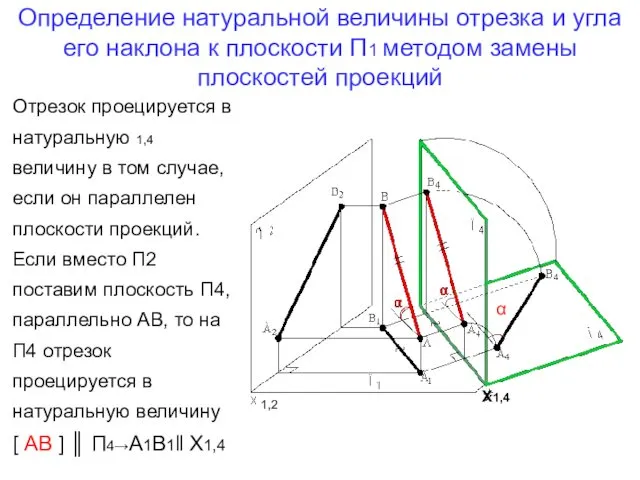
- 8. Определение натуральной величины отрезка и угла его наклона к плоскости П1 методом замены плоскостей проекций Отрезок
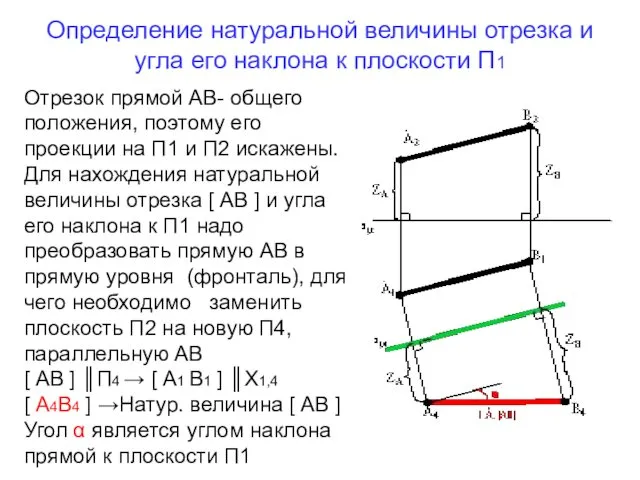
- 9. Определение натуральной величины отрезка и угла его наклона к плоскости П1 Отрезок прямой АВ- общего положения,
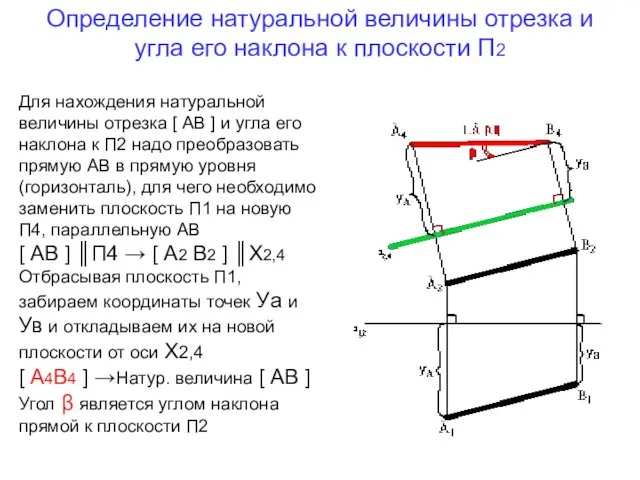
- 10. Определение натуральной величины отрезка и угла его наклона к плоскости П2 Для нахождения натуральной величины отрезка
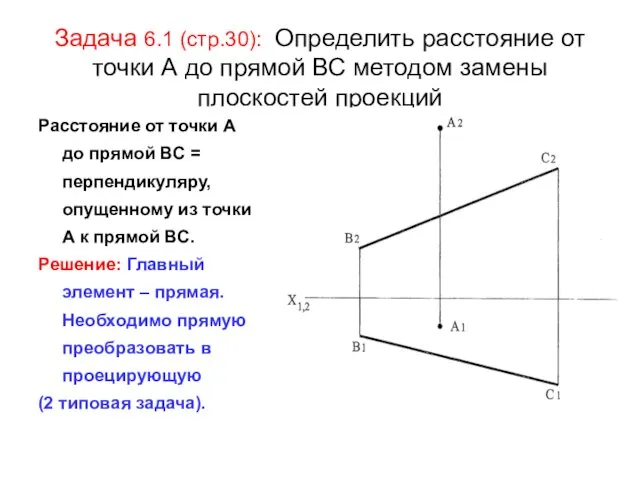
- 11. Задача 6.1 (стр.30): Определить расстояние от точки А до прямой ВС методом замены плоскостей проекций Расстояние
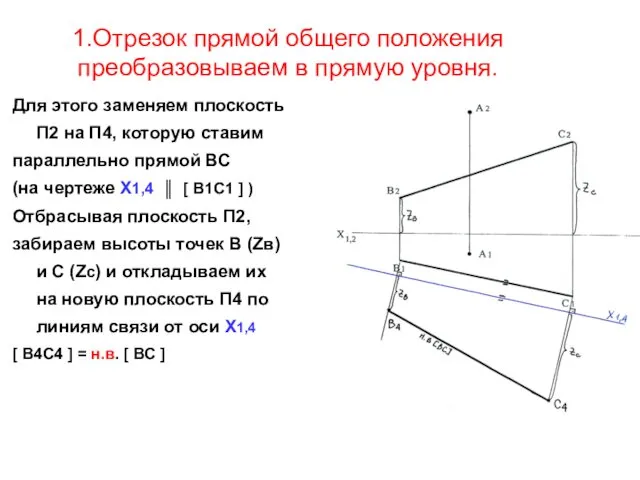
- 12. 1.Отрезок прямой общего положения преобразовываем в прямую уровня. Для этого заменяем плоскость П2 на П4, которую
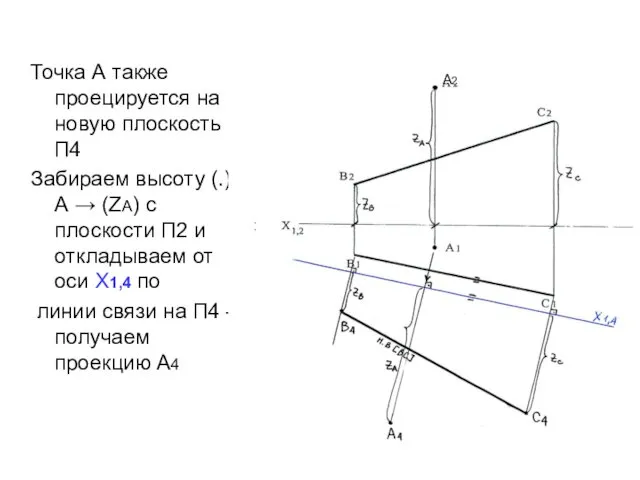
- 13. Точка А также проецируется на новую плоскость П4 Забираем высоту (.)А → (ZА) с плоскости П2
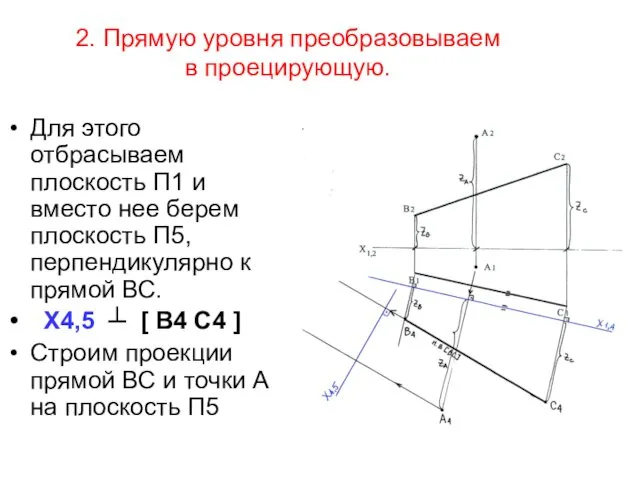
- 14. 2. Прямую уровня преобразовываем в проецирующую. Для этого отбрасываем плоскость П1 и вместо нее берем плоскость
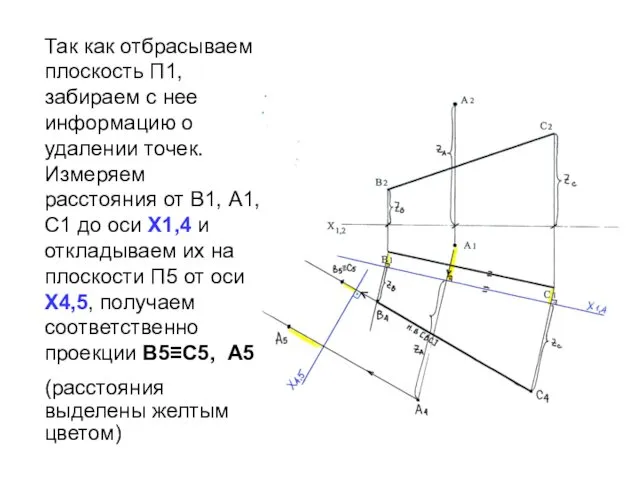
- 15. Так как отбрасываем плоскость П1, забираем с нее информацию о удалении точек. Измеряем расстояния от В1,
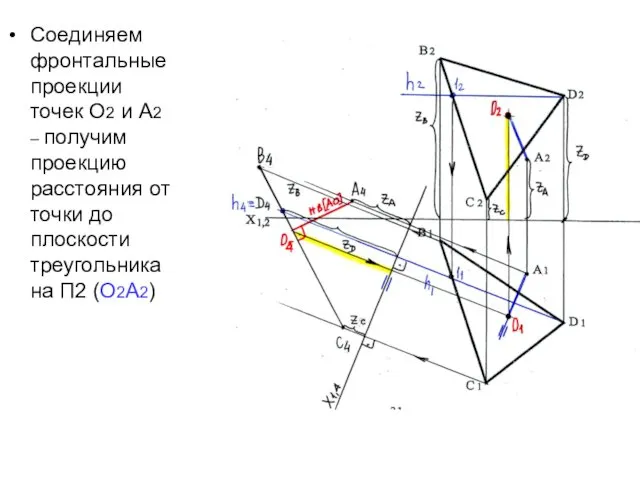
- 16. Соединяем проекции точек А5 и В5≡ С5. Получаем натуральную величину [АО] -расстояния от точки А до
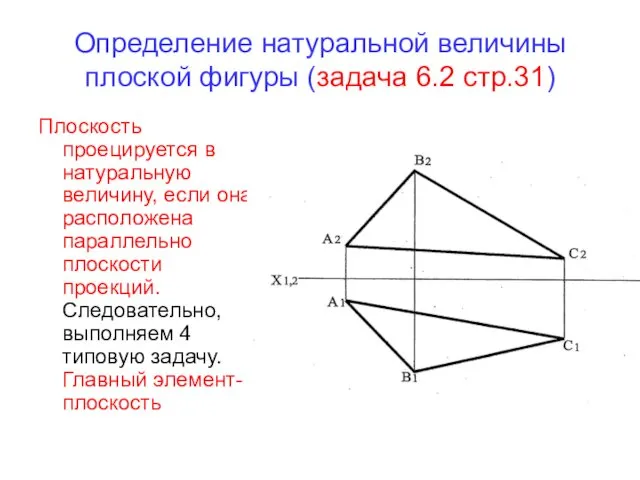
- 17. В задаче необходимо показать, как выглядят проекции отрезка [АО] на исходных плоскостях проекций: П1 и П2.
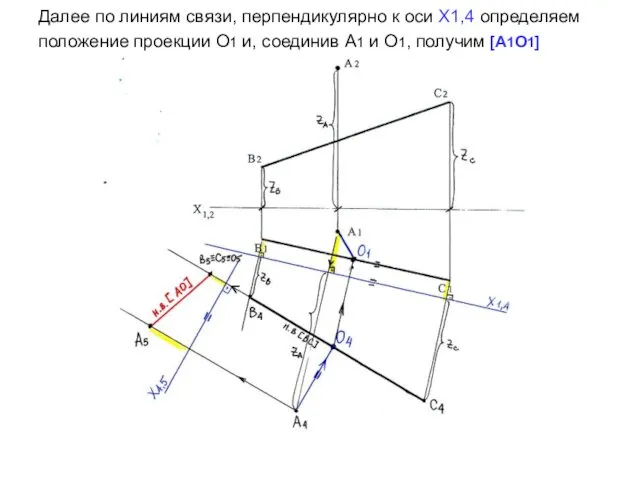
- 18. Далее по линиям связи, перпендикулярно к оси Х1,4 определяем положение проекции О1 и, соединив А1 и
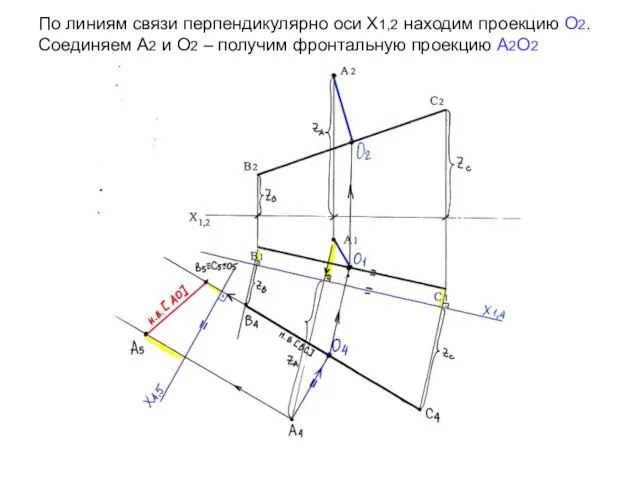
- 19. По линиям связи перпендикулярно оси Х1,2 находим проекцию О2. Соединяем А2 и О2 – получим фронтальную
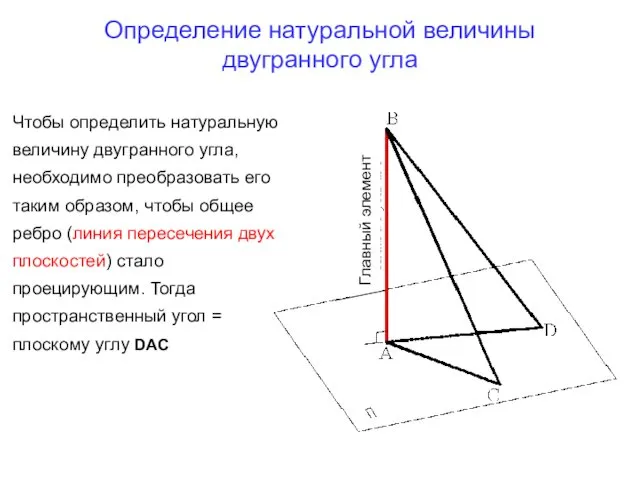
- 20. Определение натуральной величины двугранного угла Главный элемент Чтобы определить натуральную величину двугранного угла, необходимо преобразовать его
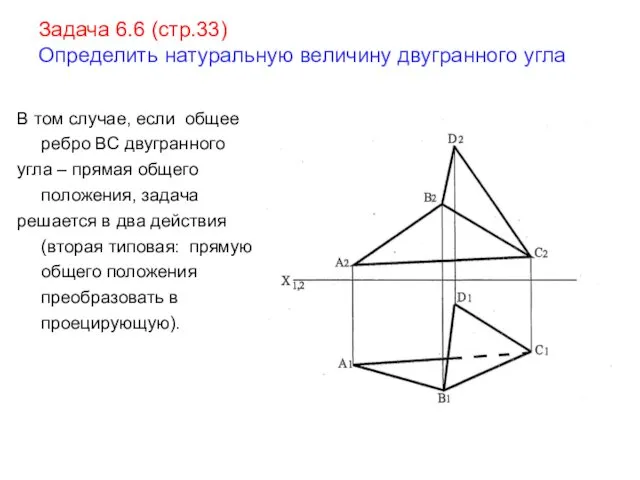
- 21. Задача 6.6 (стр.33) Определить натуральную величину двугранного угла В том случае, если общее ребро ВС двугранного
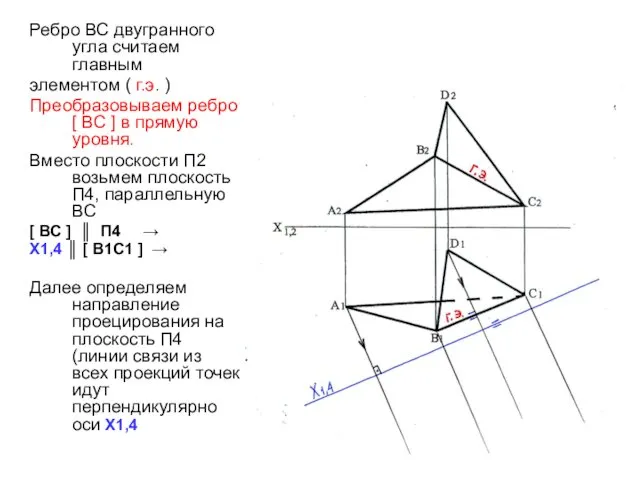
- 22. Ребро ВС двугранного угла считаем главным элементом ( г.э. ) Преобразовываем ребро [ ВС ] в
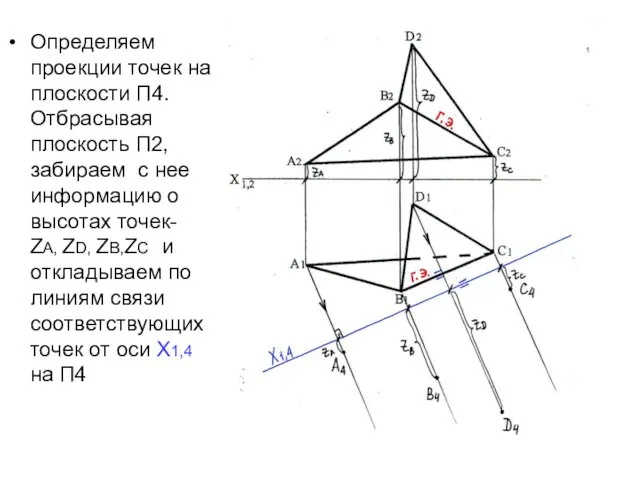
- 23. Определяем проекции точек на плоскости П4. Отбрасывая плоскость П2, забираем с нее информацию о высотах точек-
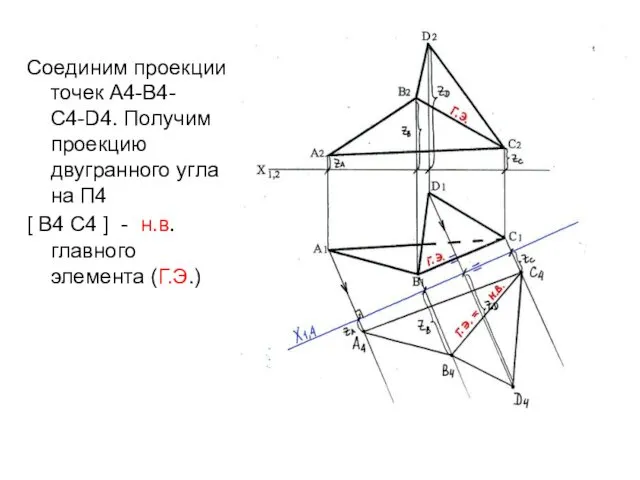
- 24. Соединим проекции точек А4-В4-С4-D4. Получим проекцию двугранного угла на П4 [ В4 С4 ] - н.в.
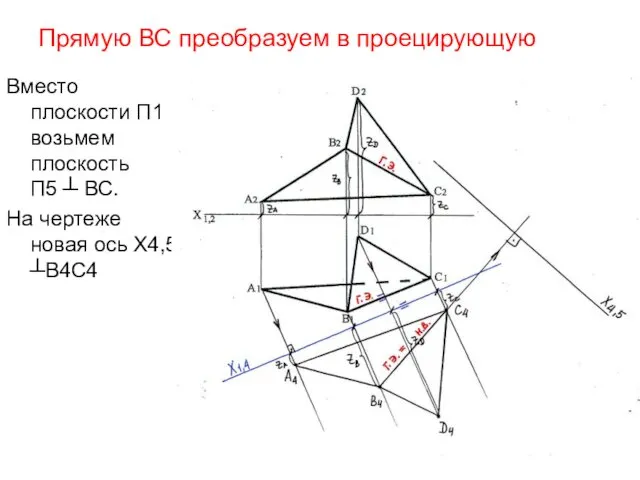
- 25. Прямую ВС преобразуем в проецирующую Вместо плоскости П1 возьмем плоскость П5 ┴ ВС. На чертеже новая
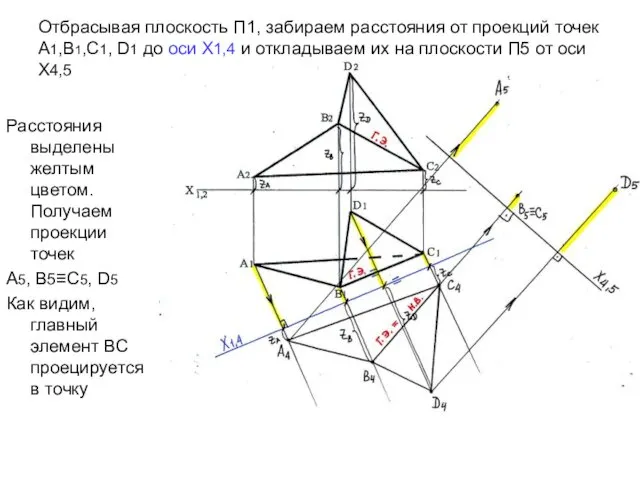
- 26. Отбрасывая плоскость П1, забираем расстояния от проекций точек А1,В1,С1, D1 до оси Х1,4 и откладываем их
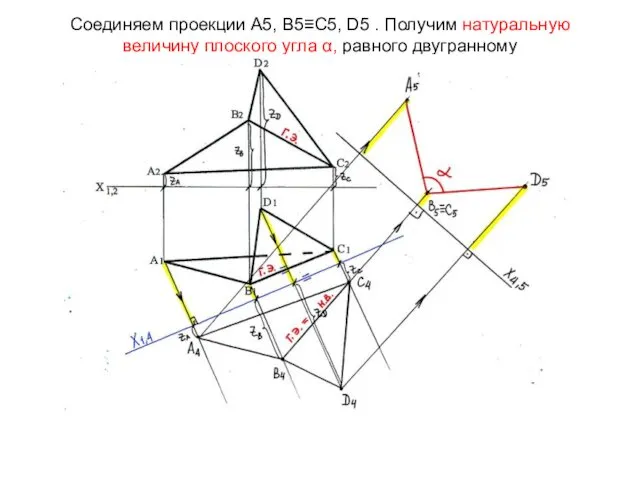
- 27. Соединяем проекции А5, В5≡С5, D5 . Получим натуральную величину плоского угла α, равного двугранному
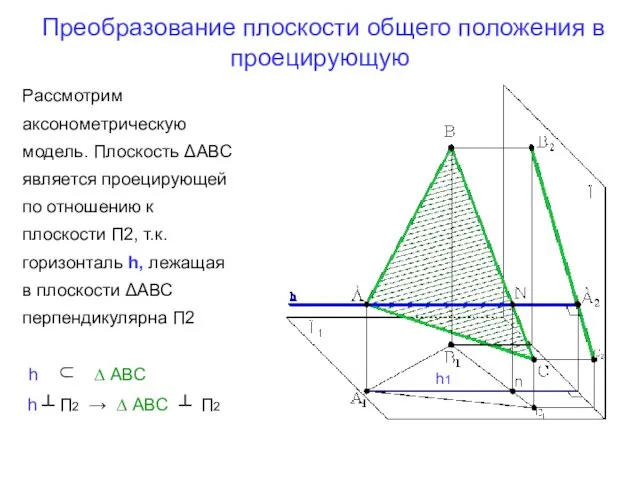
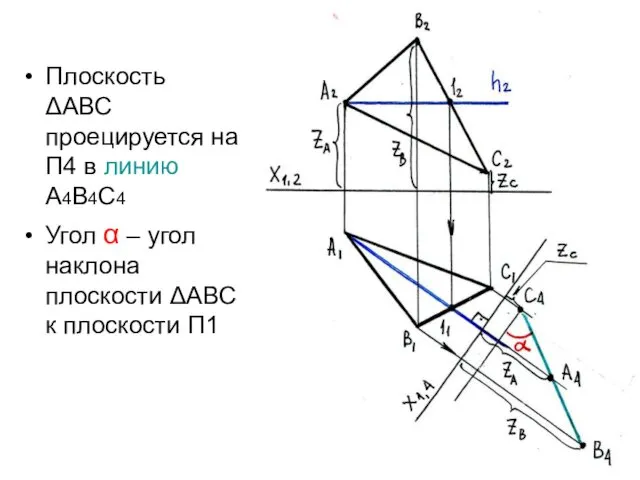
- 28. Преобразование плоскости общего положения в проецирующую Чтобы определить угол наклона плоскости общего положения к плоскости проекций,
- 29. Преобразование плоскости общего положения в проецирующую Рассмотрим аксонометрическую модель. Плоскость ΔАВС является проецирующей по отношению к
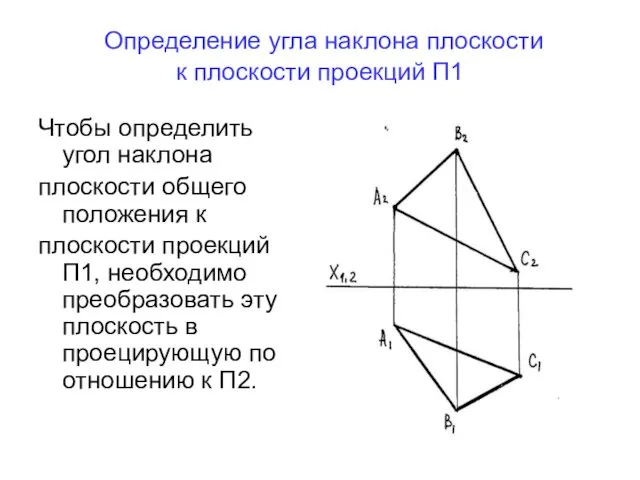
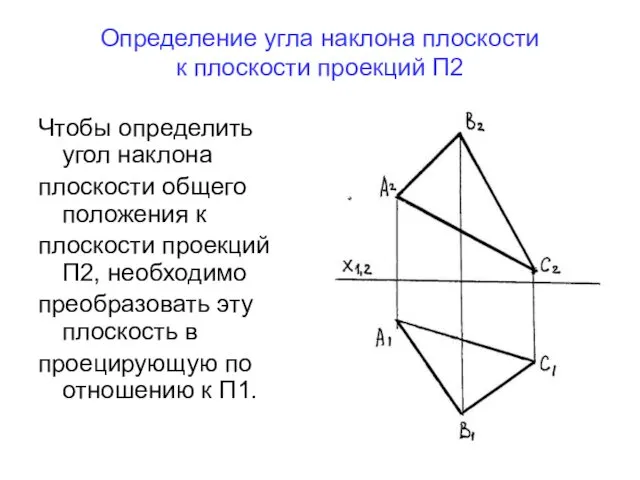
- 30. Определение угла наклона плоскости к плоскости проекций П1 Чтобы определить угол наклона плоскости общего положения к
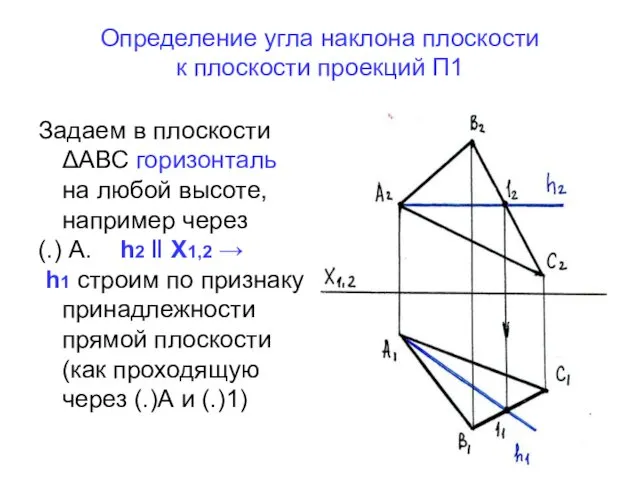
- 31. Определение угла наклона плоскости к плоскости проекций П1 Задаем в плоскости ΔАВС горизонталь на любой высоте,
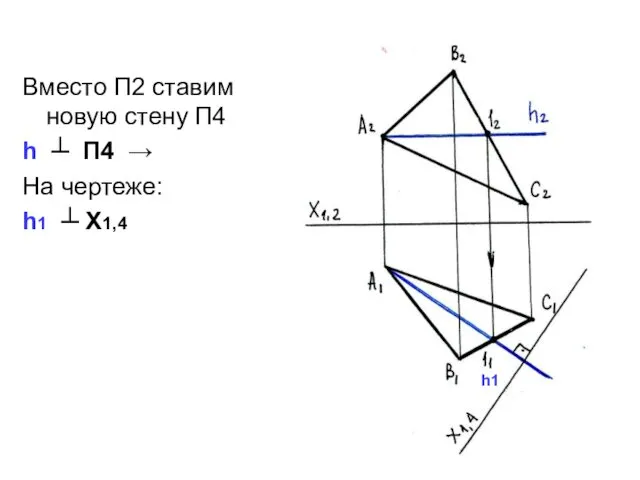
- 32. Вместо П2 ставим новую стену П4 h ┴ П4 → На чертеже: h1 ┴ Х1,4 h1
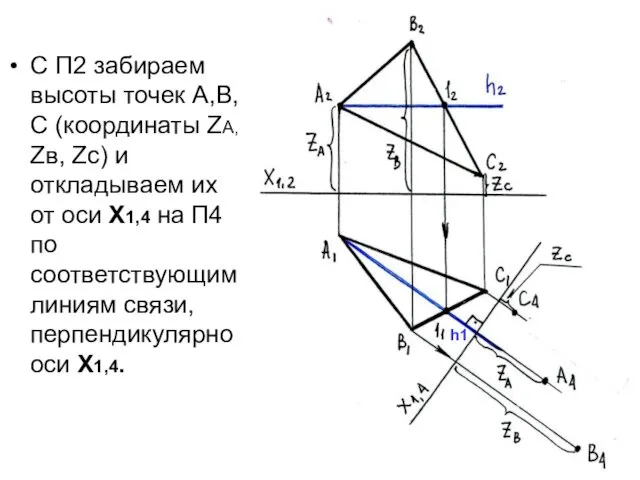
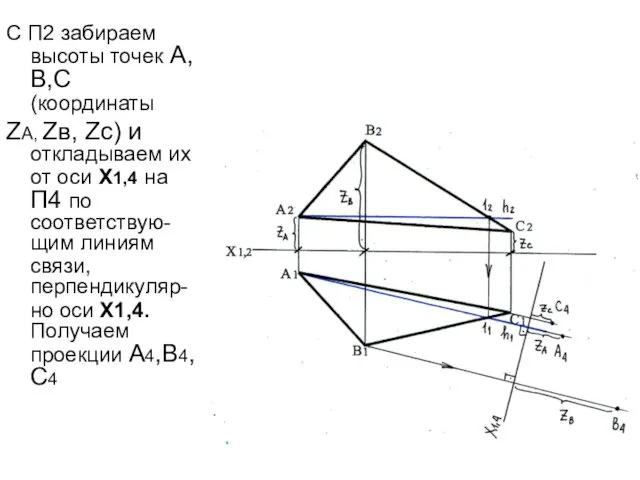
- 33. С П2 забираем высоты точек А,В,С (координаты ZА, Zв, Zс) и откладываем их от оси Х1,4
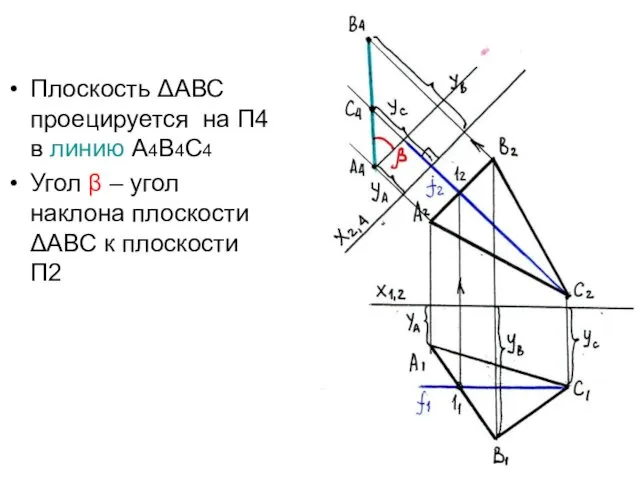
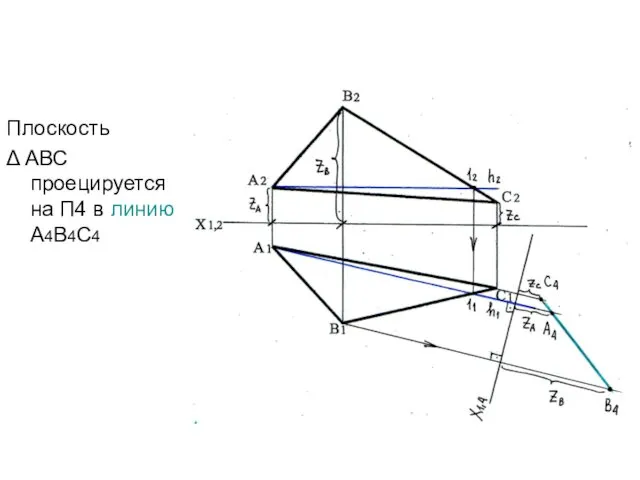
- 34. Плоскость ΔАВС проецируется на П4 в линию А4В4С4 Угол α – угол наклона плоскости ΔАВС к
- 35. Определение угла наклона плоскости к плоскости проекций П2 Чтобы определить угол наклона плоскости общего положения к
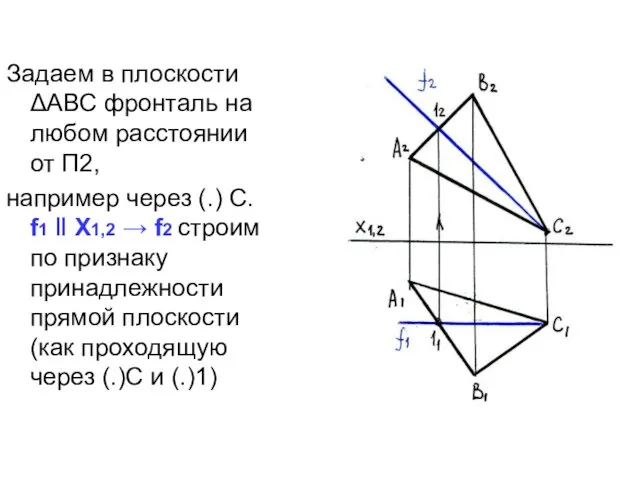
- 36. Задаем в плоскости ΔАВС фронталь на любом расстоянии от П2, например через (.) С. f1 ‖
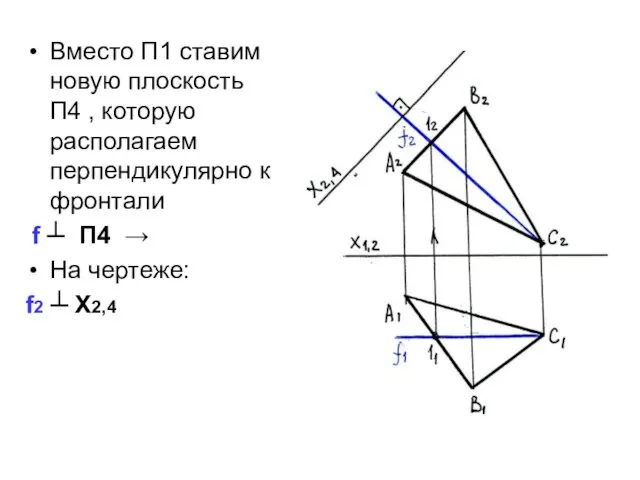
- 37. Вместо П1 ставим новую плоскость П4 , которую располагаем перпендикулярно к фронтали f ┴ П4 →
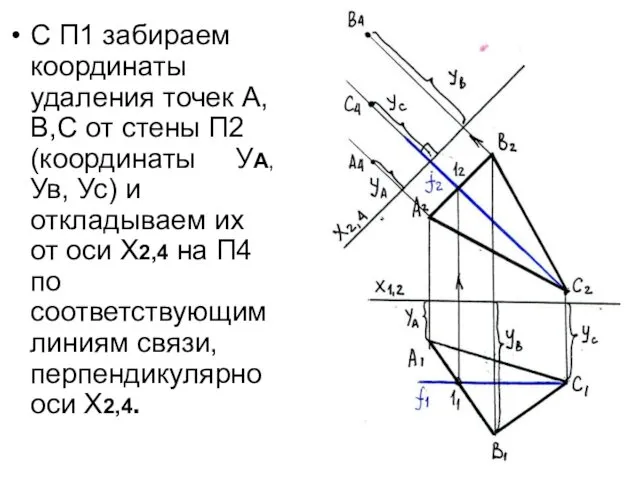
- 38. С П1 забираем координаты удаления точек А,В,С от стены П2 (координаты УА, Ув, Ус) и откладываем
- 39. Плоскость ΔАВС проецируется на П4 в линию А4В4С4 Угол β – угол наклона плоскости ΔАВС к
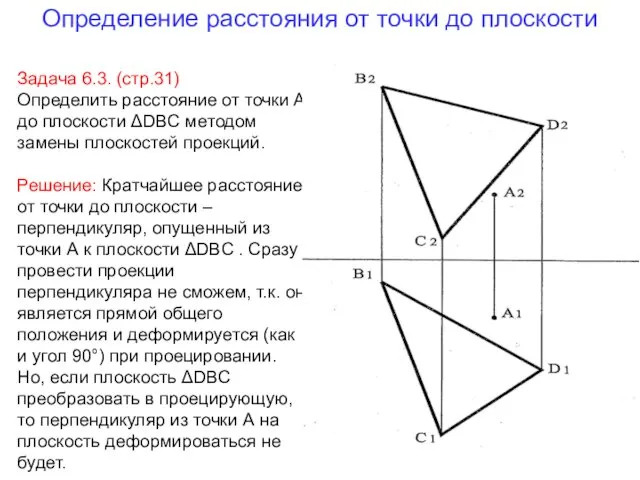
- 40. Определение расстояния от точки до плоскости Задача 6.3. (стр.31) Определить расстояние от точки А до плоскости
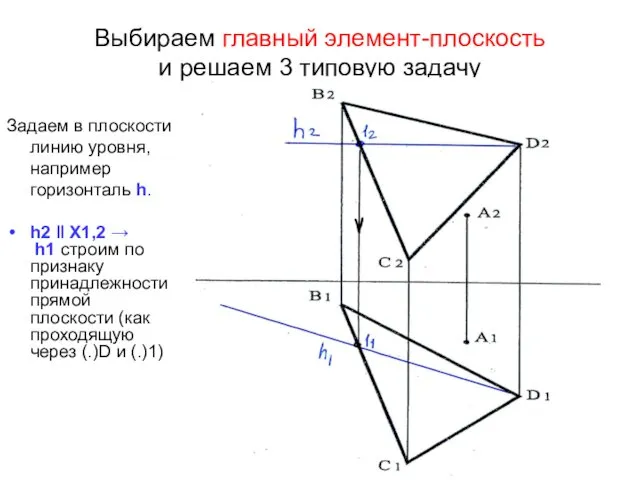
- 41. Выбираем главный элемент-плоскость и решаем 3 типовую задачу Задаем в плоскости линию уровня, например горизонталь h.
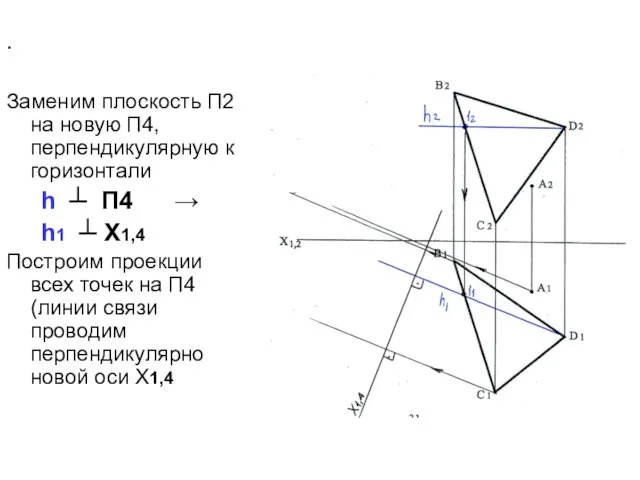
- 42. . Заменим плоскость П2 на новую П4, перпендикулярную к горизонтали h ┴ П4 → h1 ┴
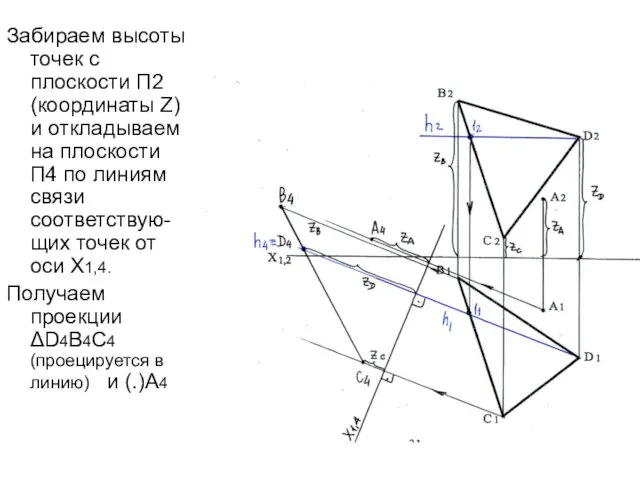
- 43. Забираем высоты точек с плоскости П2 (координаты Z) и откладываем на плоскости П4 по линиям связи
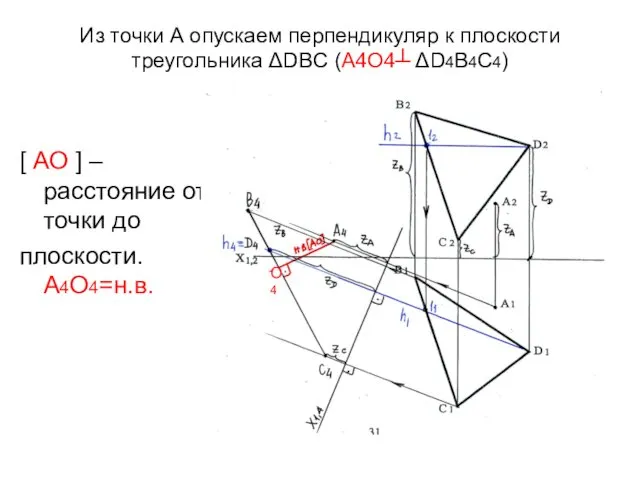
- 44. Из точки А опускаем перпендикуляр к плоскости треугольника ΔDBC (А4О4┴ ΔD4B4C4) [ АО ] – расстояние
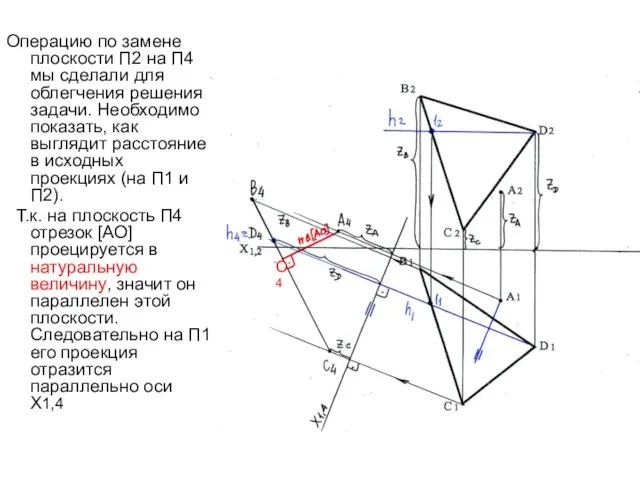
- 45. Операцию по замене плоскости П2 на П4 мы сделали для облегчения решения задачи. Необходимо показать, как
- 46. 4 Определим проекции [АО] на П1 и П2: А1О1‖Х1,4 ; По линии связи с О4 определяем
- 47. 4 Определим проекции [АО] на П2: находим проекцию О2→высота точки О на П4 и П2 одинакова
- 48. Соединяем фронтальные проекции точек О2 и А2 – получим проекцию расстояния от точки до плоскости треугольника
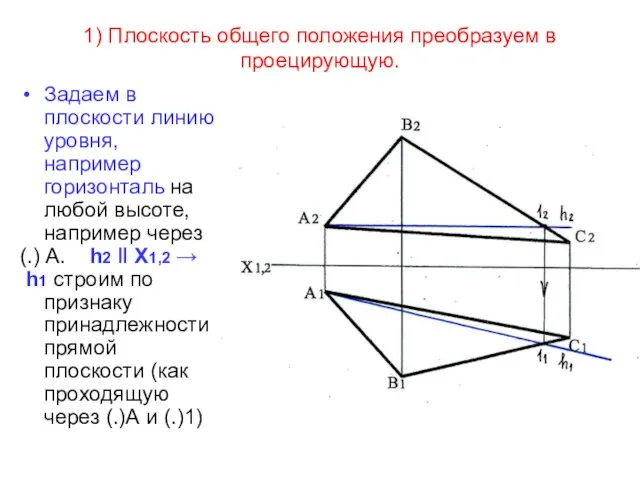
- 49. Определение натуральной величины плоской фигуры (задача 6.2 стр.31) Плоскость проецируется в натуральную величину, если она расположена
- 50. 1) Плоскость общего положения преобразуем в проецирующую. Задаем в плоскости линию уровня, например горизонталь на любой
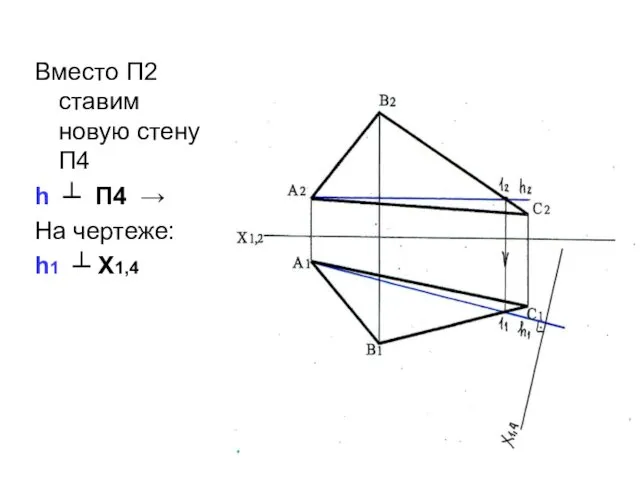
- 51. Вместо П2 ставим новую стену П4 h ┴ П4 → На чертеже: h1 ┴ Х1,4
- 52. С П2 забираем высоты точек А,В,С (координаты ZА, Zв, Zс) и откладываем их от оси Х1,4
- 53. Плоскость Δ АВС проецируется на П4 в линию А4В4С4
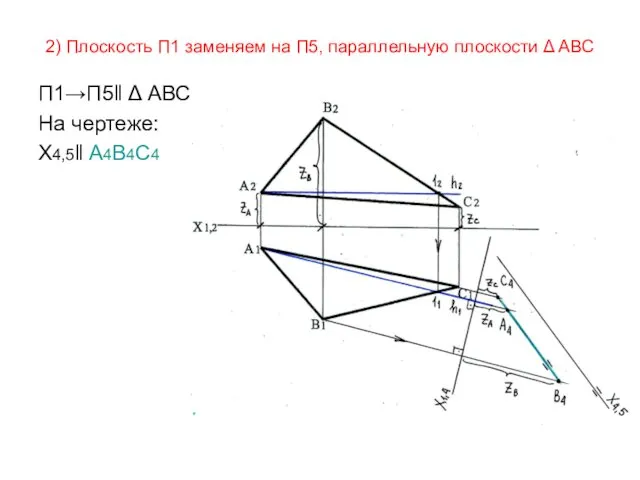
- 54. 2) Плоскость П1 заменяем на П5, параллельную плоскости Δ АВС П1→П5‖ Δ АВС На чертеже: Х4,5‖
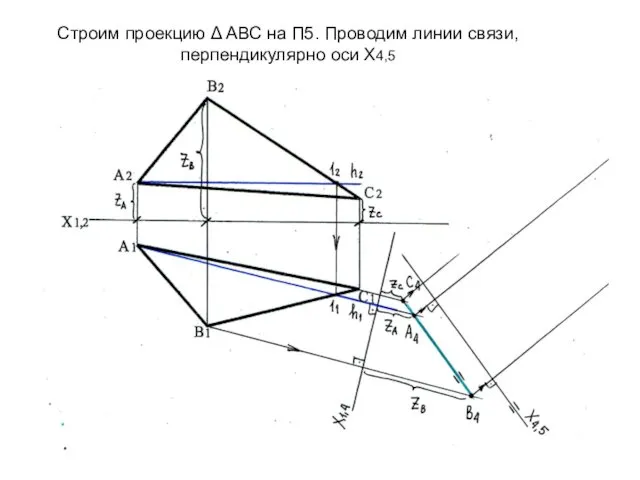
- 55. Строим проекцию Δ АВС на П5. Проводим линии связи, перпендикулярно оси Х4,5
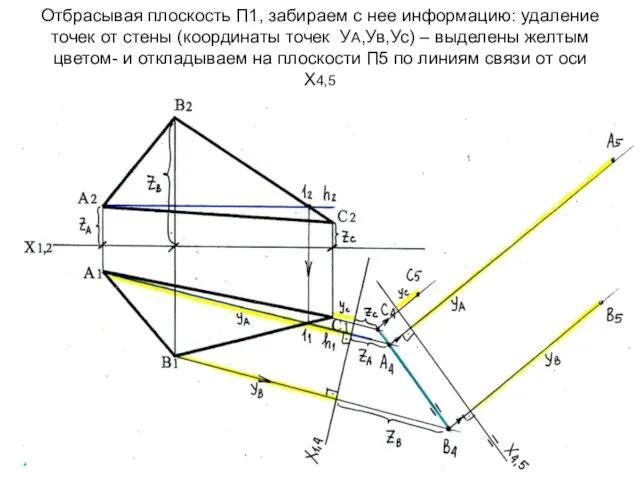
- 56. Отбрасывая плоскость П1, забираем с нее информацию: удаление точек от стены (координаты точек УА,Ув,Ус) – выделены
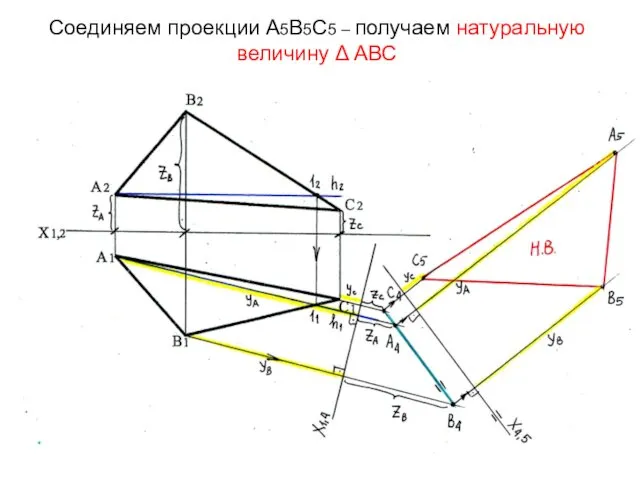
- 57. Соединяем проекции А5В5С5 – получаем натуральную величину Δ АВС
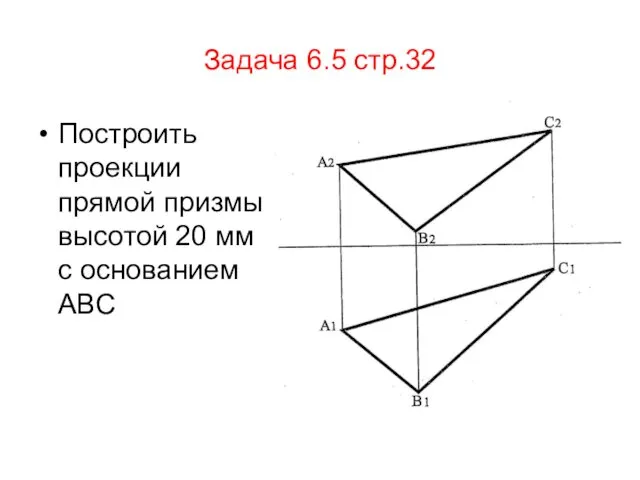
- 58. Задача 6.5 стр.32 Построить проекции прямой призмы высотой 20 мм с основанием АВС
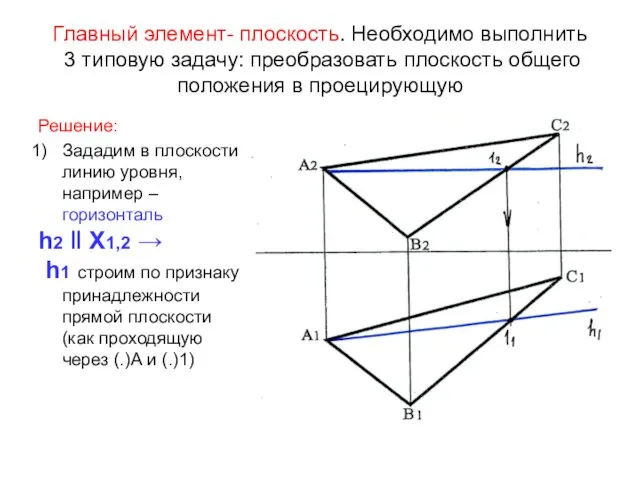
- 59. Главный элемент- плоскость. Необходимо выполнить 3 типовую задачу: преобразовать плоскость общего положения в проецирующую Решение: Зададим
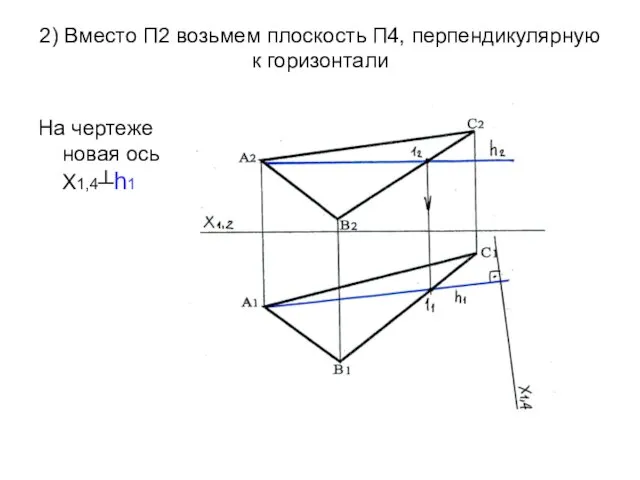
- 60. 2) Вместо П2 возьмем плоскость П4, перпендикулярную к горизонтали На чертеже новая ось Х1,4┴h1
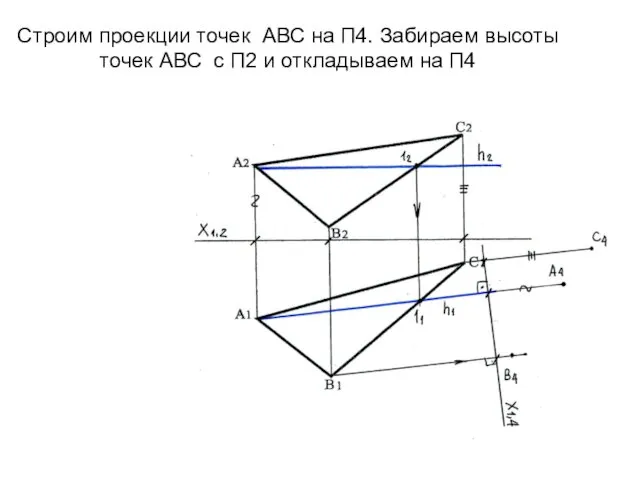
- 61. Строим проекции точек АВС на П4. Забираем высоты точек АВС с П2 и откладываем на П4
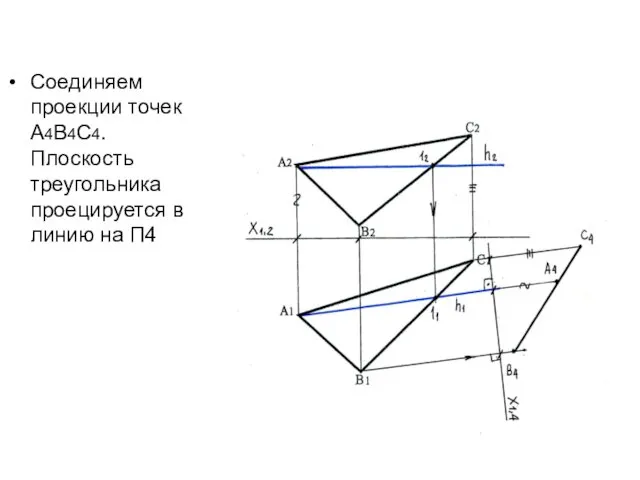
- 62. Соединяем проекции точек А4В4С4. Плоскость треугольника проецируется в линию на П4
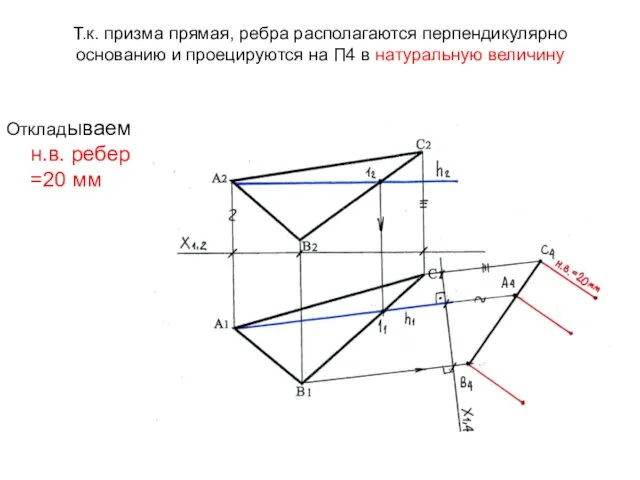
- 63. Т.к. призма прямая, ребра располагаются перпендикулярно основанию и проецируются на П4 в натуральную величину Откладываем н.в.
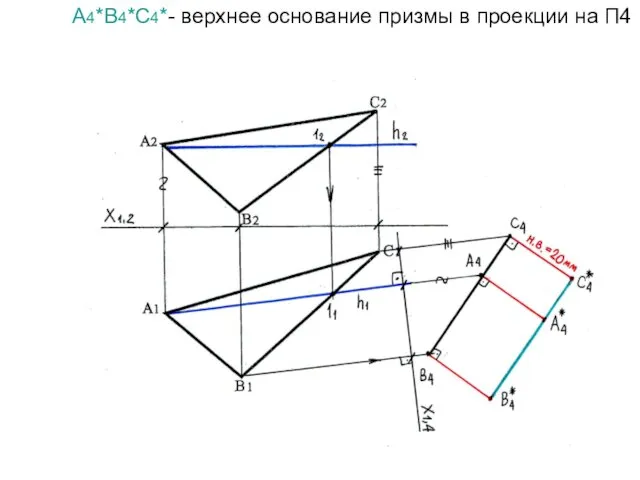
- 64. А4*В4*С4*- верхнее основание призмы в проекции на П4
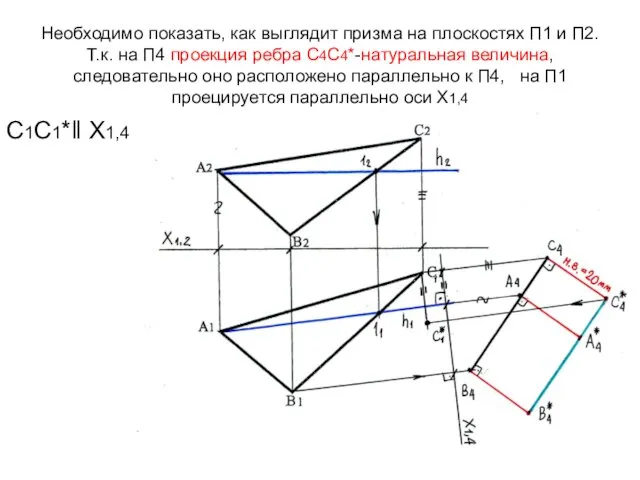
- 65. Необходимо показать, как выглядит призма на плоскостях П1 и П2. Т.к. на П4 проекция ребра С4С4*-натуральная
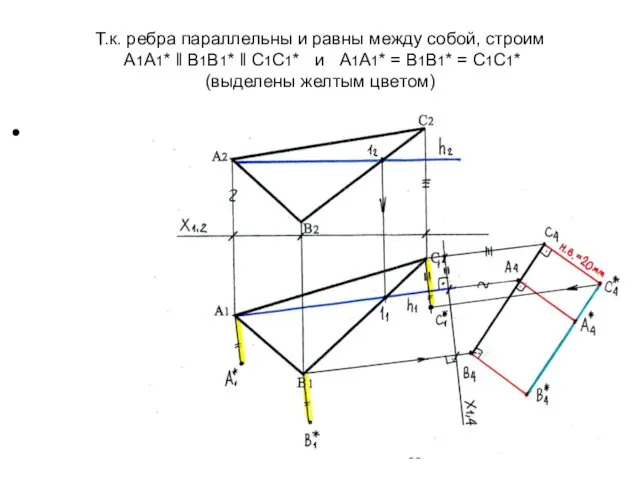
- 66. Т.к. ребра параллельны и равны между собой, строим А1А1* ‖ В1В1* ‖ С1С1* и А1А1* =
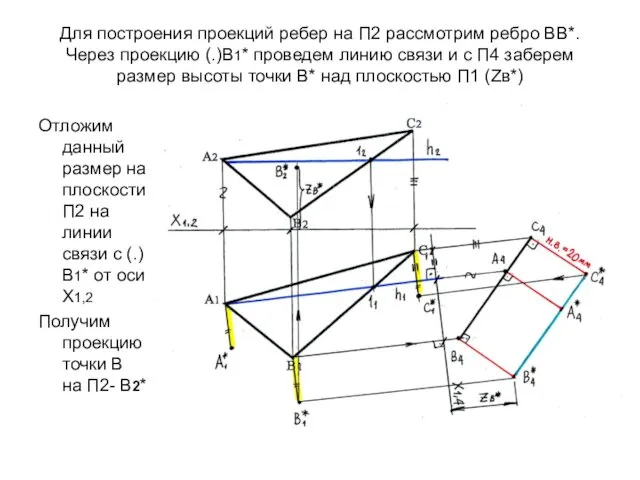
- 67. Для построения проекций ребер на П2 рассмотрим ребро ВВ*. Через проекцию (.)В1* проведем линию связи и
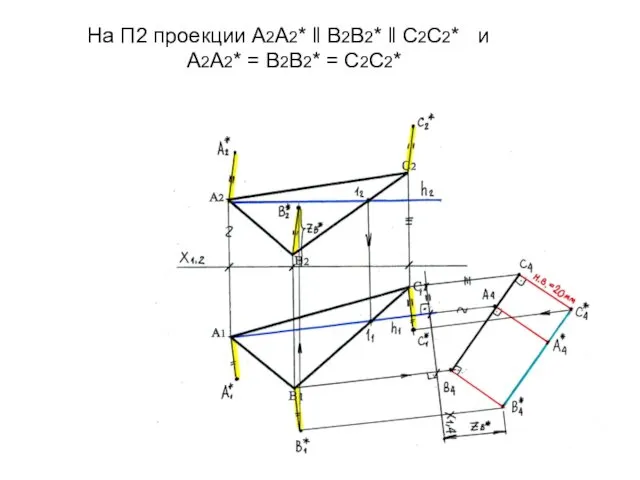
- 68. На П2 проекции А2А2* ‖ В2В2* ‖ С2С2* и А2А2* = В2В2* = С2С2*
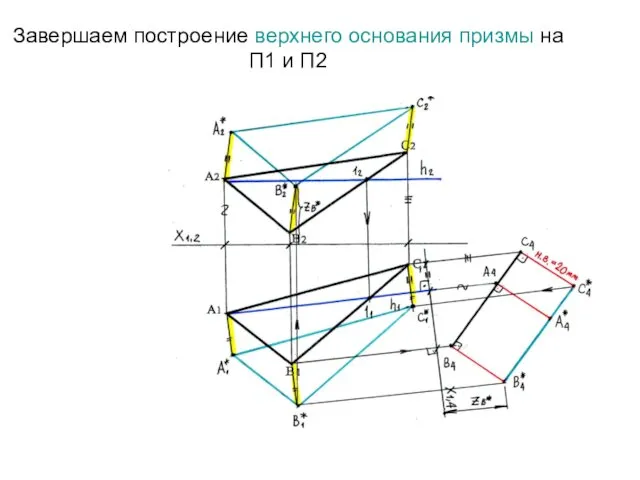
- 69. Завершаем построение верхнего основания призмы на П1 и П2
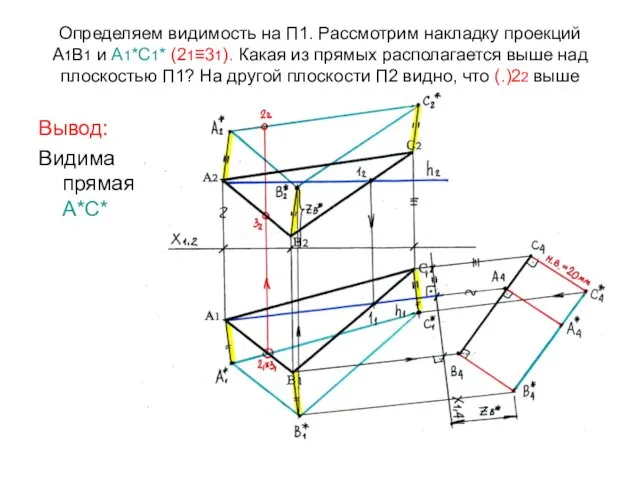
- 70. Определяем видимость на П1. Рассмотрим накладку проекций А1В1 и А1*С1* (21≡31). Какая из прямых располагается выше
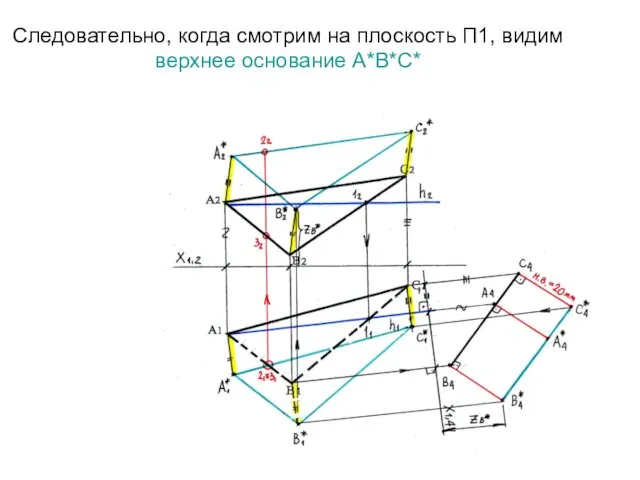
- 71. Следовательно, когда смотрим на плоскость П1, видим верхнее основание А*В*С*
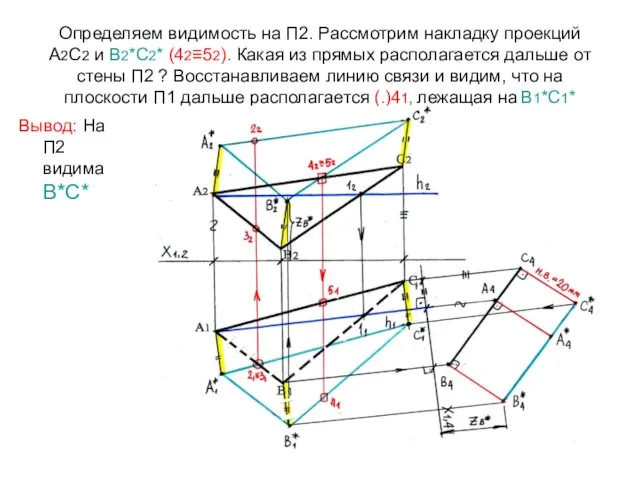
- 72. Определяем видимость на П2. Рассмотрим накладку проекций А2С2 и В2*С2* (42≡52). Какая из прямых располагается дальше
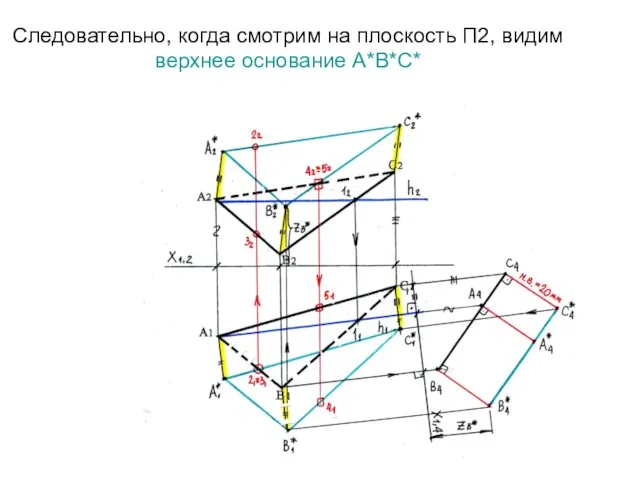
- 73. Следовательно, когда смотрим на плоскость П2, видим верхнее основание А*В*С*
- 75. Скачать презентацию





![Соединяем проекции точек А5 и В5≡ С5. Получаем натуральную величину [АО]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/491269/slide-15.jpg)
![В задаче необходимо показать, как выглядят проекции отрезка [АО] на исходных](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/491269/slide-16.jpg)

![4 Определим проекции [АО] на П1 и П2: А1О1‖Х1,4 ; По](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/491269/slide-45.jpg)
![4 Определим проекции [АО] на П2: находим проекцию О2→высота точки О](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/491269/slide-46.jpg)
 Нанесение размеров на чертежах. Применение и обозначение масштабов
Нанесение размеров на чертежах. Применение и обозначение масштабов Работа над ошибками. Что мы упустили в графической работе?
Работа над ошибками. Что мы упустили в графической работе? Неразъёмные соединения. (Лекция 12)
Неразъёмные соединения. (Лекция 12) Проект планировки участка линейного объекта улично-дорожной сети – районы Алексеевский и Ростокино
Проект планировки участка линейного объекта улично-дорожной сети – районы Алексеевский и Ростокино Построение изображений. Лабораторная работа № 3
Построение изображений. Лабораторная работа № 3 Сечения и разрезы
Сечения и разрезы Фасад. Креслення
Фасад. Креслення Аксонометрические проекции
Аксонометрические проекции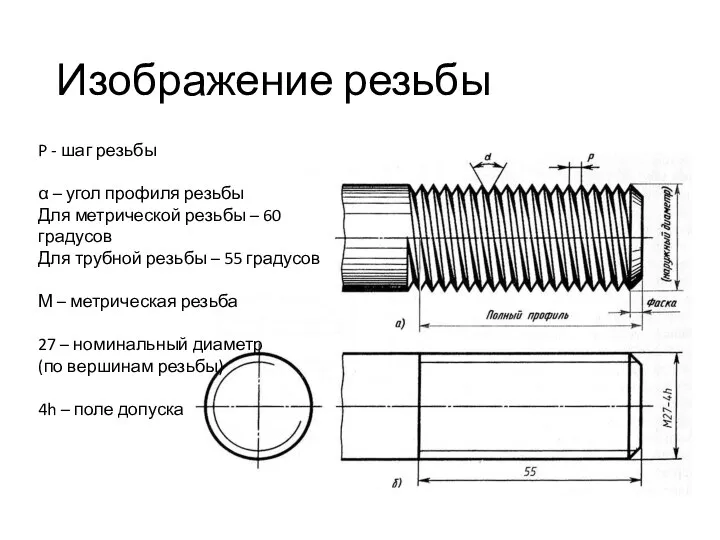 Изображение резьбы
Изображение резьбы Точка роста. Типы линий
Точка роста. Типы линий Условности и упрощения пpи выполнении изображении
Условности и упрощения пpи выполнении изображении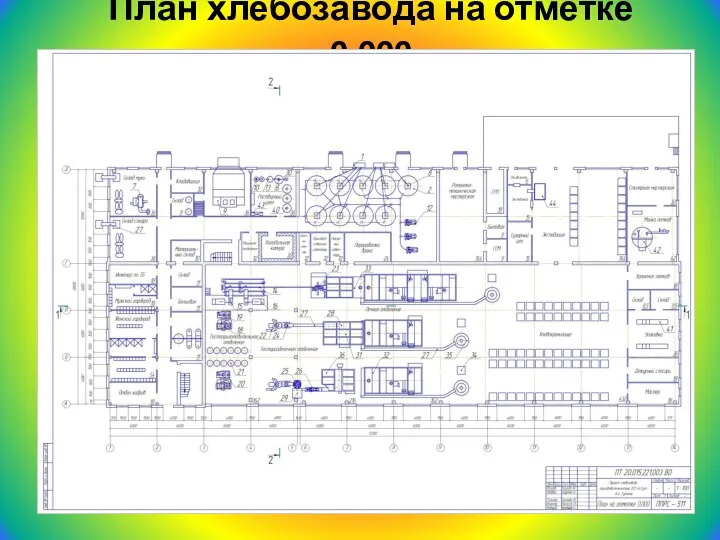 Проектирования предприятия отрасли
Проектирования предприятия отрасли Графический материал к отчету по учебной практике
Графический материал к отчету по учебной практике Электронный учебный курс по дисциплине ОП.01 Инженерная графика
Электронный учебный курс по дисциплине ОП.01 Инженерная графика Шероховатость и волнистость поверхностей
Шероховатость и волнистость поверхностей Выполнение и чтение чертежей
Выполнение и чтение чертежей Схемы и их выполнение
Схемы и их выполнение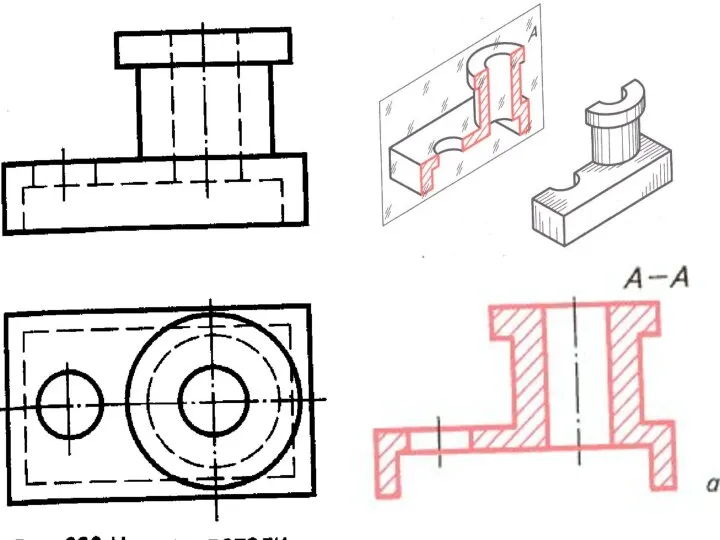 Разрезы
Разрезы Графическая документация
Графическая документация Конструкторская и технологическая документация. Урок 5-6
Конструкторская и технологическая документация. Урок 5-6 Элементы, конструктивные схемы и классификация зданий
Элементы, конструктивные схемы и классификация зданий Виды и типы схем. Код схемы. Правила выполнения структурных схем
Виды и типы схем. Код схемы. Правила выполнения структурных схем Сопряжения. Применение сопряжений в конструировании
Сопряжения. Применение сопряжений в конструировании Инженерная графика
Инженерная графика Образы МИП
Образы МИП Пересечение поверхности плоскостью
Пересечение поверхности плоскостью Графические изображения
Графические изображения Резьба
Резьба