Modeling and forecasting. Volatility

Outline

Introduction: Why ARCH?
ARCH Models
Extensions: GARCH, T-GARCH, Q-GARCH, GARCH-M, Box-Cox GARCH
Estimation
Multivariate GARCH

1. Introduction: Why ARCH?

Why ARCH?

ARMA and VAR models are based on the conditional mean

Some example series: UST10Y

Dow Jones

Symmetric Shocks?

Homoskedastic?

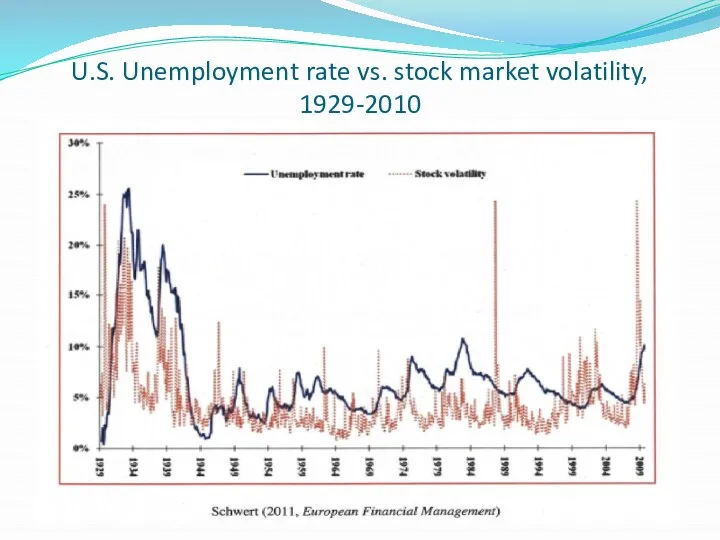
U.S. Unemployment rate vs. stock market volatility, 1929-2010

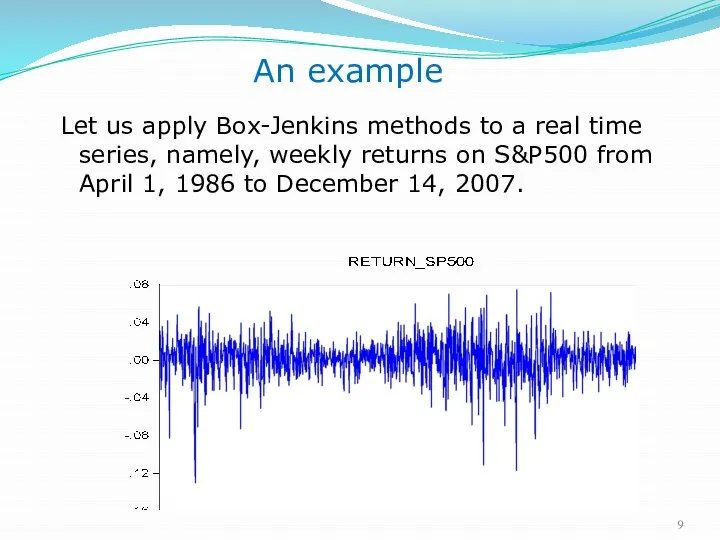
U.S. Realized Volatility (kernel based) 1997-2009

An example

Let us apply Box-Jenkins methods to a real time series,

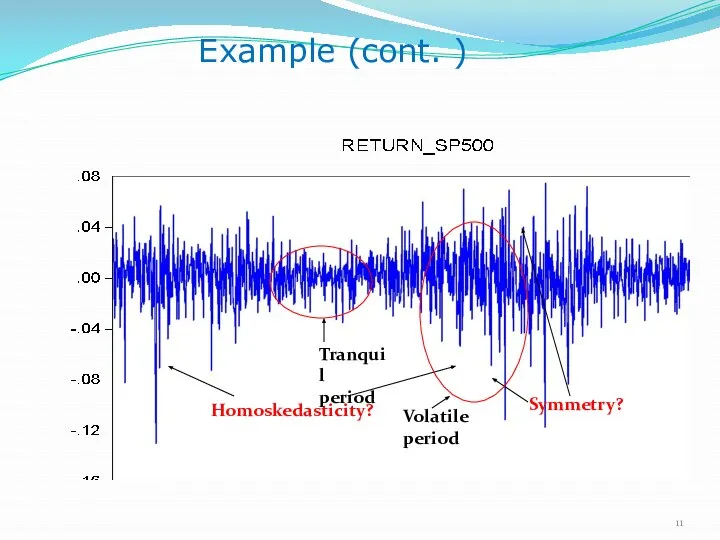
Example (cont.)

Note:

Tranquil
period

Volatile period

Example (cont. )

Homoskedasticity?

Symmetry?

Tranquil
period

Volatile period

Example (cont.)

Both ACF and PACF are flat, suggesting p=0 and q=0

Example (cont. )

Look at the histogram and some summary statistics of

Skewness

The shape of a uni-modal distribution can be symmetric or

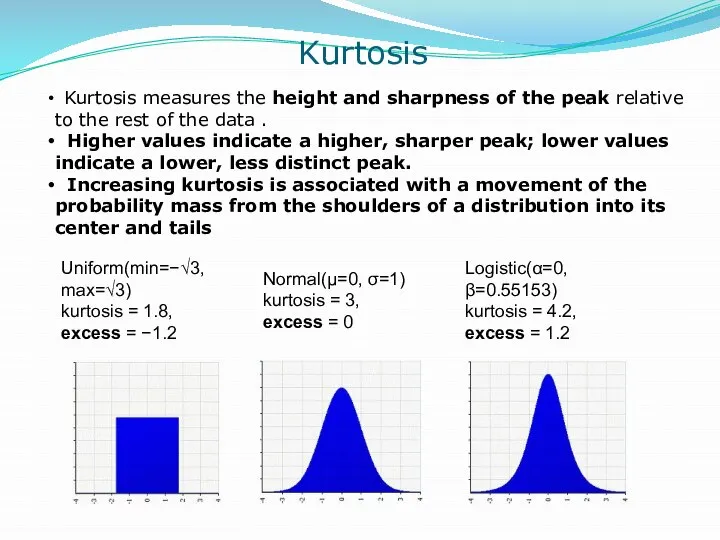
Kurtosis

Kurtosis measures the height and sharpness of the peak relative

Remarks

Gaussian ARMA models are not able to generate asymmetric or fat-tailed

Example

Variance of financial returns is often referred to as volatility.
To understand

EViews Example – Daily S&P 500 Returns

When we learn about GARCH(1,1)…

We’ll be able to make squared residuals white noise

Quality of TGARCH predictions: 1% quantiles, VaR(0.01), from August 1, 2007

2. ARCH Models

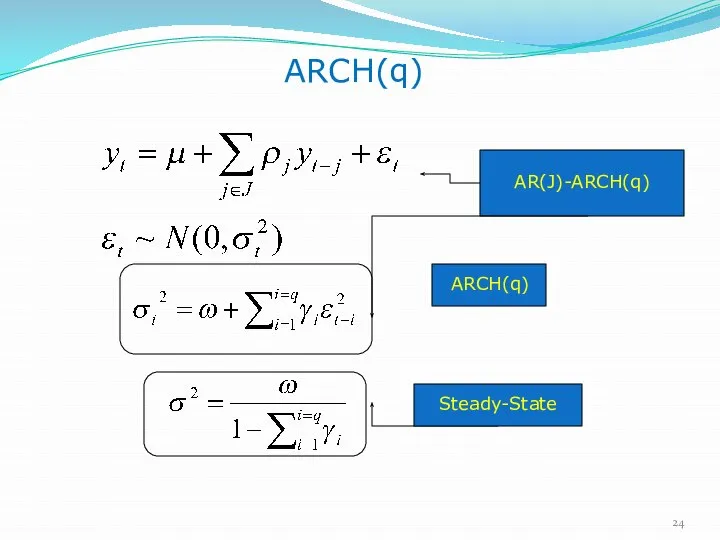
ARCH(q)

AR(J)-ARCH(q)

AR(J)-ARCH(q)

ARCH(q)

Steady-State

A special case: ARCH(1)
Properties [It-1 = y1,..,yt-1]
with the AR coefficient

Testing for the ARCH effects
Regress on .
Calculate , which is

3. Extensions

GARCH(p,q)

AR(J)-ARCH(q)

AR(J)-GARCH(p,q)

GARCH(p,q)

Steady-State

Additivity
No negativity

GARCH(1,1)

The most popular ARCH-type model

Volatility ( )

VaR=1.645σ

Properties of GARCH(1,1)
1. follows an ARMA(1,1) with the AR coefficient ,

I-GARCH

If the coefficients of the GARCH model sum to 1, then

Impulse

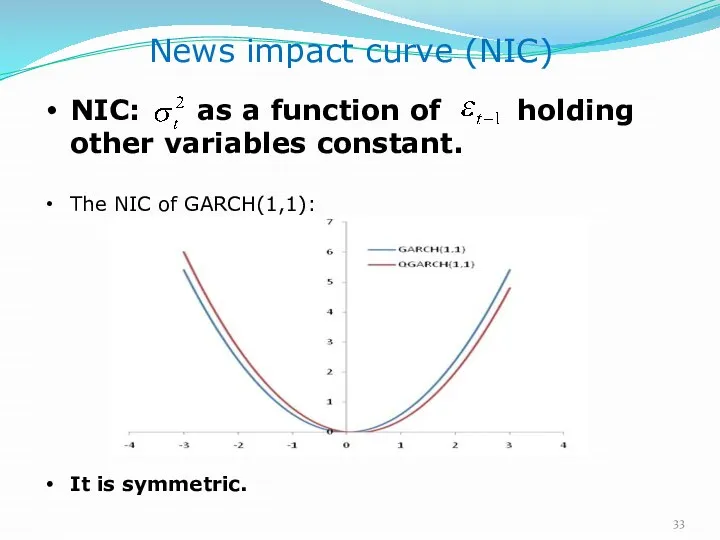
NIC: as a function of holding other variables constant.
The NIC

Student t -- GARCH(1,1)
where
Compared to the Gaussian GARCH, the Student t-GARCH

T-GARCH (Asymmetry)
NIC is asymmetric.
If , bad news has a larger

IRFs

T-GARCH (Asymmetry)

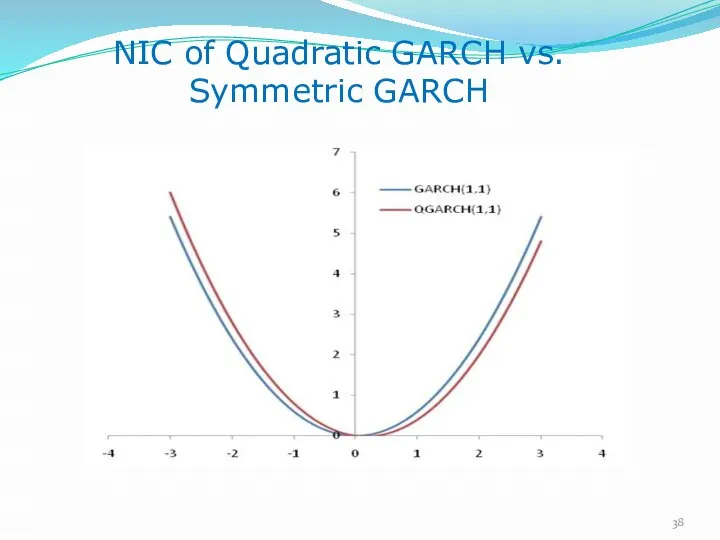
Asymmetric Volatility

Q(uadratic)-GARCH (Asymmetry)

NIC of Quadratic GARCH vs.
Symmetric GARCH

GARCH-M

An important application of the ARCH-type models is in modeling

Box-Cox GARCH(1,1)
We model the power transformation of volatility.
As long

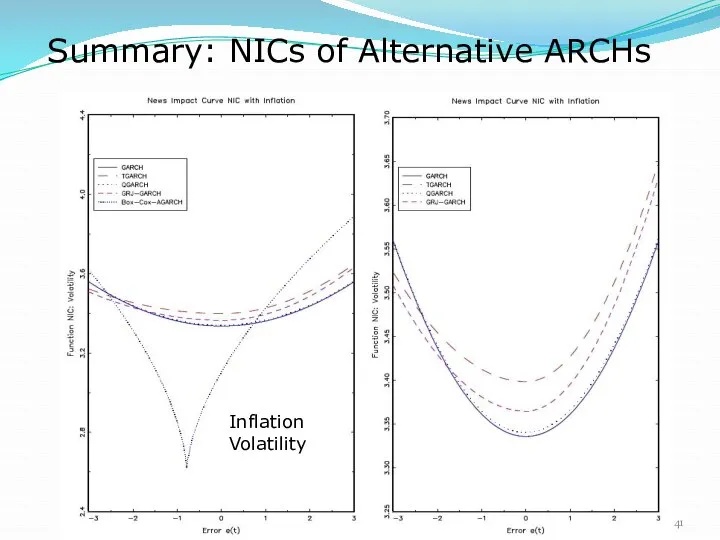
Summary: NICs of Alternative ARCHs

Inflation Volatility

Summing up (see Appendix for an expanded list)

Asymmetric Models

Non linear

3. Estimation

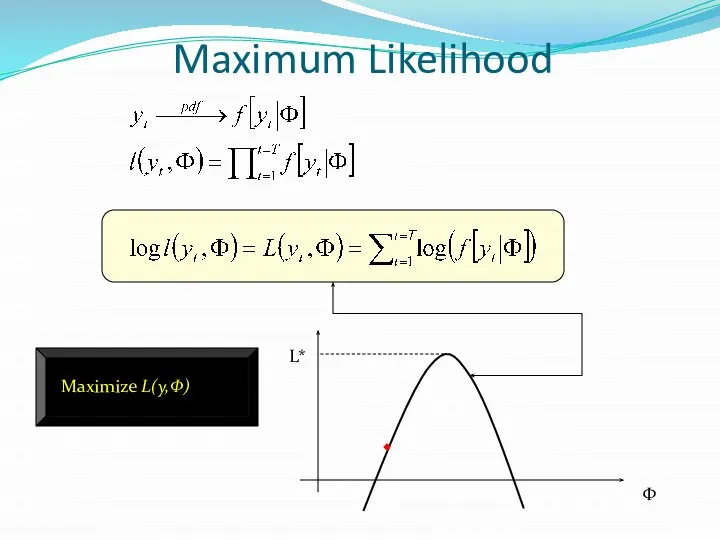
Maximum Likelihood

Maximize L(y,Φ)

Φ

L*

Maximum Likelihood (continued)

The maximum likelihood decomposes in a “mean” and

Optimization

Newton’s Method
Stochastic Newton Method

Gradient and Hill Climbing Techniques

Multiple Solutions

Monte Carlo
Genetic Algorithms

4. Multivariate models

Multivariate GARCH Models

A natural extension of the time-varying variance models based

Vech Model (2 variables)
The conditional variance of each variable depends on

BEKK Model
C is a NxN lower triangular matrix of unknown parameters

Diagonal Vech Model (2 variables)
Variances and covariances are GARCH(1,1)
Parameters are now

CCC
(Constant Conditional Correlation) Model

3 variables
The correlation coefficients are all time

An extension: VAR + CCC

3 variables

A further extension:
VAR + CCC+ GARCH-M

Interactions between Markets
Contagion

An example of volatility “contagion’’

5. Application: Value-at-Risk (VaR)

VaR

What is the most I can lose on an investment?
VaR

Value-at-Risk (VaR)

VaR summarizes the expected maximum loss over a time horizon

Value-at-Risk (VaR) - Continued

The simplest assumption: daily gains/losses are normally distributed

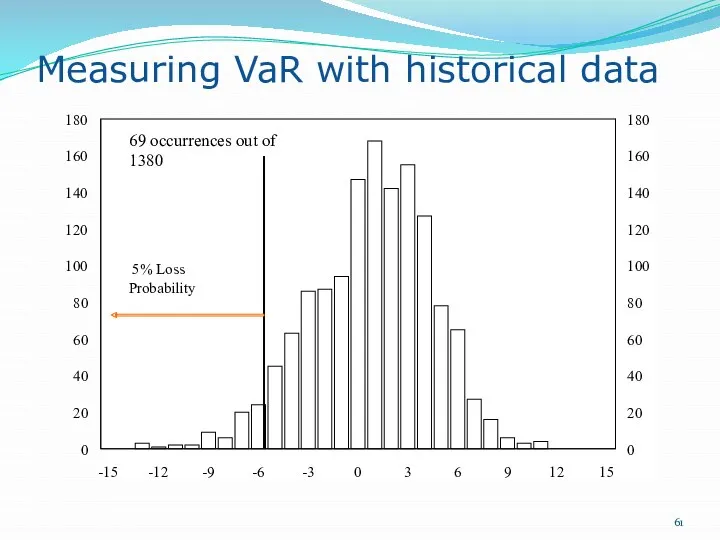
Measuring VaR with historical data

0

20

40

60

80

100

120

140

160

180

-15

-12

-9

-6

-3

0

3

6

9

12

15

0

20

40

60

80

100

120

140

160

180

Probability

Assuming a Normal distribution

Mean Return (μ)

Standard Deviation (σ)

Assume that asset returns

VaR with Normally Distributed Returns

The probability of the return falling below

Portfolio VaR

When we have more than one asset in our portfolio

An Example

Let us consider the following investment
US$200 million invested in 5-year

An Example (cont.)

Suppose we want to compute the 95% VaR.
The

An Example of Portfolio VaR

Two securities
30-year zero-coupon U.S. Treasury bond
5-year zero-coupon

An Example of Portfolio VaR

95% confidence level
30 year zero VaR
1.65

VaR of the Portfolio

Suppose the correlation between the two bonds is

The problem with Normality: Kurtosis

Extreme asset price changes occur more often

Fat Tails and underestimation of VaR

If we assume that returns are

Backtesting

Model backtesting involves systematic comparisons of the calculated VaRs with the

Relevance: Basel VaR Guidelines

VaR computed daily, holding period is 10 days.
The

Summing up

A host of research has examined
a. how best to

Thank you!

Appendix – GARCH univariate families

Source: Bollerslev 2010, Engle Festschrift

APPENDIX II – Software