Содержание
- 2. Область определения функции. Асимптоты. Точки разрыва. Четность, нечетность функции. Периодичность. Точки пересечения с осями координат. Интервалы
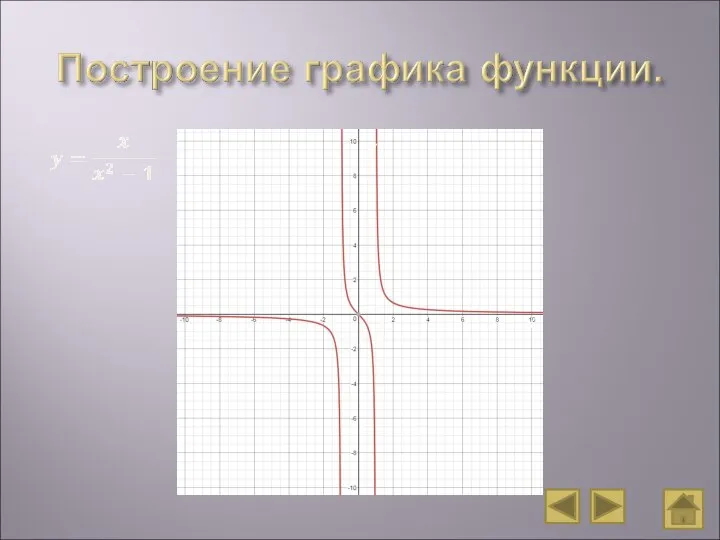
- 3. Областью определения функции y=f(x), заданной аналитически, называют множество всех действительных значений независимой переменной х, для каждого
- 4. Наклонные и горизонтальные асимптоты: , где . Вертикальные асимптоты следует искать в точках разрыва функции. Точки
- 5. Если f(-x)=f(x), то функция f(x) называется четной. График четной функции симметричен относительно оси ординат (оси Oy).
- 6. С Ох: y=0. Решить F(x)=0. С Оу: x=0. Найти y=F(0). Числовые промежутки, на которых функция сохраняет
- 7. Для этого: вычисляем производную f’(x) и находим критические точки функции, т.е. точки, в которых f’(x)=0 или
- 8. если производная меняет знак при переходе через критическую точку xo є D, то xo – точка
- 9. Для этого: вычисляем вторую производную f’’(x) и находим точки, принадлежащие области определения функции, в которых f''(x)=0
- 10. если f’’(x) если f’’(x)>0, то график функции имеет выпуклость вниз; если вторая производная меняет знак при
- 11. Y X
- 13. Скачать презентацию









 Строение атомов, магнетизм микрочастиц, молекулярные спектры
Строение атомов, магнетизм микрочастиц, молекулярные спектры Презентация по физике "21-22. Двигатель внутреннего сгорания" - скачать бесплатно
Презентация по физике "21-22. Двигатель внутреннего сгорания" - скачать бесплатно Атомдардың рентгендік спектрі. (Лекция14)
Атомдардың рентгендік спектрі. (Лекция14) Презентация по физике "Развитие энергетики республики Башкортостан" - скачать
Презентация по физике "Развитие энергетики республики Башкортостан" - скачать  Законы электродинамики. Их физический смысл
Законы электродинамики. Их физический смысл Импульс.Закон сохранения импульса ФИЗИКА – 9 класс
Импульс.Закон сохранения импульса ФИЗИКА – 9 класс Движение в поле силы тяжести. Свободное падение
Движение в поле силы тяжести. Свободное падение Тематический проект «Виды теплообмена»
Тематический проект «Виды теплообмена»  Никель-кадмиевые аккумуляторные батареи
Никель-кадмиевые аккумуляторные батареи Разумное потребление батареек
Разумное потребление батареек Радиоактивность. Строение атома
Радиоактивность. Строение атома Өткен сабақты игеру барысын тексеру
Өткен сабақты игеру барысын тексеру Аналогии физических свойств сегнетоэлектрических и ферромагнитных кристаллов
Аналогии физических свойств сегнетоэлектрических и ферромагнитных кристаллов Контрольная работа по теме Кинематика
Контрольная работа по теме Кинематика Презентация по физике "Производство передача и использование электроэнергии" - скачать
Презентация по физике "Производство передача и использование электроэнергии" - скачать  Источники звука. Звуковые колебания
Источники звука. Звуковые колебания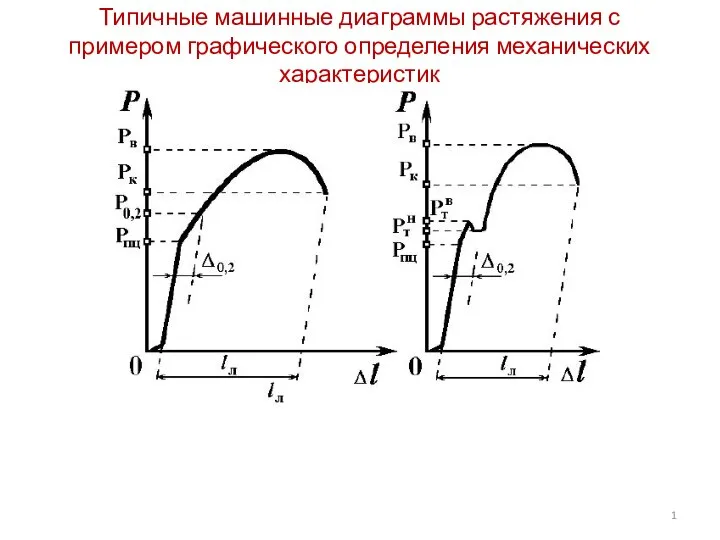 Типичные машинные диаграммы растяжения с примером графического определения механических характеристик
Типичные машинные диаграммы растяжения с примером графического определения механических характеристик Планетарная модель атома. Ядерная модель атома. Квантовые постулаты Бора
Планетарная модель атома. Ядерная модель атома. Квантовые постулаты Бора Оптика. Прохождение света через границу раздела двух сред. (Лекция 3)
Оптика. Прохождение света через границу раздела двух сред. (Лекция 3) Применение в фармацевтическом анализе рефрактометрии, поляриметрии, полярографии
Применение в фармацевтическом анализе рефрактометрии, поляриметрии, полярографии СВОБОДНЫЕ И ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ. УСЛОВИЯ ВОЗНИКНОВЕНИЯ СВОБОДНЫХ КОЛЕБАНИЙ.
СВОБОДНЫЕ И ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ. УСЛОВИЯ ВОЗНИКНОВЕНИЯ СВОБОДНЫХ КОЛЕБАНИЙ. Полевая геофизика. Магниторазведка (лекция 2 )
Полевая геофизика. Магниторазведка (лекция 2 ) Фазированные антенные решетки и их назначение. Задача адаптации в общем виде
Фазированные антенные решетки и их назначение. Задача адаптации в общем виде Основи гемодинаміки
Основи гемодинаміки Ауыстырмалы-төкпелі пункттардағы жүктерді тиеп-түсіру жұмыстарының технологиясы және механикалары
Ауыстырмалы-төкпелі пункттардағы жүктерді тиеп-түсіру жұмыстарының технологиясы және механикалары Презентация по физике "Радиоактивность в физике" - скачать
Презентация по физике "Радиоактивность в физике" - скачать  Електростатичне поле
Електростатичне поле  Проектирование системы обеспечения теплового режима космического полета
Проектирование системы обеспечения теплового режима космического полета