Содержание
- 2. ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ
- 3. В 1824 году французом Араго было обнаружено, что ко-лебания свободно подвешенной магнитной стрелки затухают значительно быстрее,
- 4. Фарадей провел ряд опытов. На немагнитный стержень намотаны два куска медного про-вода. Один(1) подсоединен к батарее
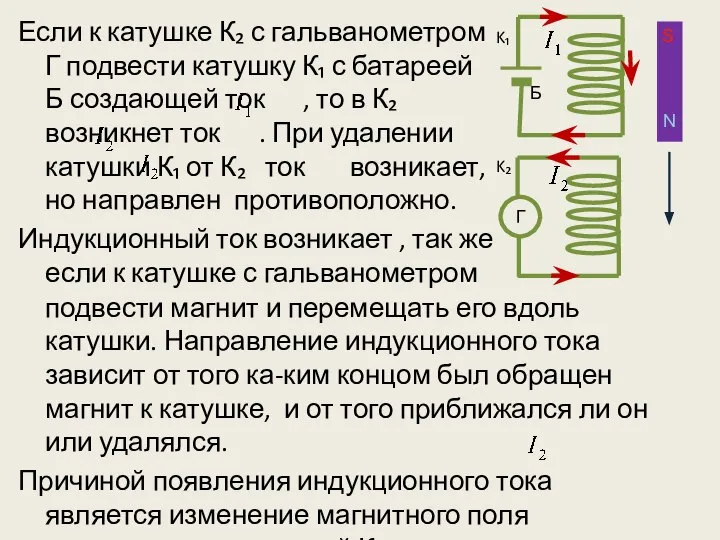
- 5. Если к катушке К₂ с гальванометром Г подвести катушку К₁ с батареей Б создающей ток ,
- 6. ЗАКОН ФАРАДЕЯ
- 7. ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ Открытое Фарадеем явление получило название : ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ – возникновение электродвижущей силы в проводнике
- 8. ЗАКОН ЭЛЕКТРОМАГНИТНОЙ ИНДУКЦИИ ФАРАДЕЯ ЭДС электромагнитной индукции в контуре численно рав-на и противоположна по знаку скорости
- 9. ПРАВИЛО ЛЕНЦА Знак «-» – показывает что увеличение потока вызывает ЭДС индукции меньше нуля то есть
- 10. Для объяснения возникновения ЭДС индукции в непод-вижных проводниках Максвелл предположил, что вся-кое переменное магнитное поле возбуждает
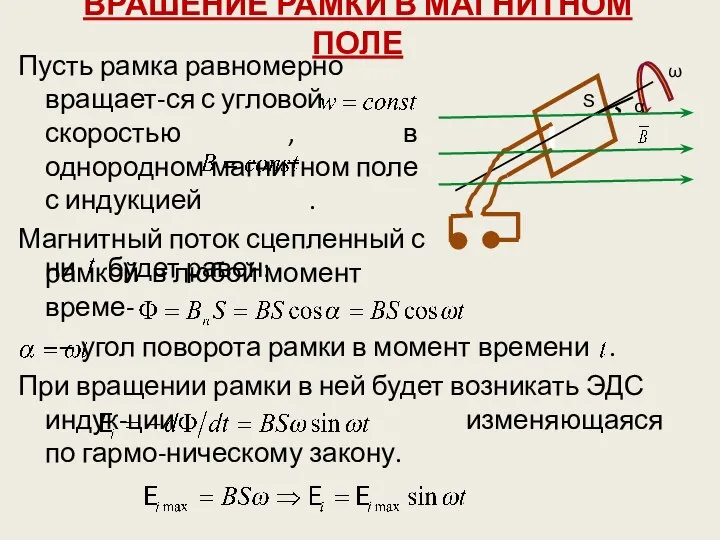
- 11. ВРАШЕНИЕ РАМКИ В МАГНИТНОМ ПОЛЕ Пусть рамка равномерно вращает-ся с угловой скоростью , в однородном магнитном
- 12. Если в однородном магнитном поле вращается рамка, то в ней возникает переменная ЭДС изменяющаяся по гармоническому
- 13. ВИХРЕВЫЕ ТОКИ (ТОКИ ФУКО) Индукционный ток возникает не только в тонких проводах, но и в массивных
- 14. лить по правилу Ленца: если первичный ток увеличи-вается ( ) то токи Фуко направлены против на-правления
- 15. ИНДУКТИВНОСТЬ КОНТУРА САМОИНДУКЦИЯ ВЗАИМНАЯ ИНДУКЦИЯ ТРАНСФОРМАТОРЫ
- 16. ИНДУКТИВНОСТЬ. САМОИНДУКЦИЯ Электрический ток текущий в контуре создает вокруг се-бя электромагнитное поле, индукция которого про-порциональна току.
- 17. Единица измерения индуктивности – Генри (Гн). 1 Гн – индуктивность такого контура, магнитный поток самоиндукции которого
- 18. ЭДС САМОИНДУКЦИИ Индуктивность контура зависит в общем случае только от геометрической формы, размеров и магнитной про
- 19. Знак «-» показывает, что наличие индуктивности в конту-ре приводит к замедлению изменения тока в нём. Если
- 20. ТОКИ ПРИ РАЗМЫКАНИИ И ЗАМЫКАНИИ ЦЕПИ При всяком изменении силы тока в проводящем контуре возникает ЭДС
- 21. по правилу Ленца уменьшению тока. В каждый момент времени ток определяется законом Ома: Интегрируя это выражение
- 22. ется ток в цепи при размыкании. При замыкании цепи помимо внешней ЭДС ,возникает ЭДС самоиндукции препятствующая
- 23. ВЗАИМНАЯ ИНДУКЦИЯ Рассмотрим два неподвижных кон-тура 1 и 2 расположенных близко друг от друга. В контуре
- 24. Аналогично, при протекании в контуре 2 тока получим: Явление возникновения ЭДС в одном из контуров, при
- 25. Рассчитаем взаимную индуктивность двух катушек, намотанных на об-щий тороидальный сердечник. Магнитная индукция поля, создава- емая первой
- 26. Так как потокосцепление создается током то: Если вычислить магнитный поток создаваемый катуш-кой 2 сквозь катушку 1,
- 27. ТРАНСФОРМАТОРЫ Впервые трансформаторы были сконструированы русскими эле-ктротехником П.Н. Яблочковым (1847-1894) и физиком И.Ф. Уса- гиным (1855-1919).
- 28. полностью локализованный в железном сердечнике, а значит, целиком пронизывающий витки вторичной обмотки. Изменение этого потока вызывает
- 29. ЭДС взаимной индукции возникающая во вторичной об-мотке: Сравнив значения ЭДС взаимной и самоиндукций получим: – ЭДС
- 31. Скачать презентацию


























 Атмосферное оптическое явление - гало
Атмосферное оптическое явление - гало Тракторы МТЗ-82
Тракторы МТЗ-82 Проектирование ТРДДФ для многоцелевого истребителя с модификацией маслосистемы
Проектирование ТРДДФ для многоцелевого истребителя с модификацией маслосистемы Негативное воздействие электромагнитного излучения на организм человека
Негативное воздействие электромагнитного излучения на организм человека Устройство, техническое обслуживание и ремонт системы смазки грузового автомобиля КамАЗ 4310
Устройство, техническое обслуживание и ремонт системы смазки грузового автомобиля КамАЗ 4310 Машина переменного тока. Лекция 15
Машина переменного тока. Лекция 15 Диэлектриктердегі электр өрісі үшін
Диэлектриктердегі электр өрісі үшін Физические свойства воды в разных агрегатных состояниях
Физические свойства воды в разных агрегатных состояниях Опыт Э.Резерфорда по строению атома
Опыт Э.Резерфорда по строению атома Исследование зависимости силы тока в проводнике от напряжения на его концах. Лабораторная работа
Исследование зависимости силы тока в проводнике от напряжения на его концах. Лабораторная работа Термодинамикалық жүйе, процесс және тепе-теңдік
Термодинамикалық жүйе, процесс және тепе-теңдік Волновая оптика. Поляризация света. Тепловое излучение (Лекция 3)
Волновая оптика. Поляризация света. Тепловое излучение (Лекция 3) Создание источника электричества из овощей и фруктов
Создание источника электричества из овощей и фруктов Электропроводность полупроводников
Электропроводность полупроводников Физика 8 класс.
Физика 8 класс.  Самостоятельная работа 66 урок
Самостоятельная работа 66 урок Механика. Глава 3. Работа и энергия
Механика. Глава 3. Работа и энергия Монохроматоры. Аппаратура в спектрофотометрических методах анализа
Монохроматоры. Аппаратура в спектрофотометрических методах анализа Виштовхувальна сила. Закон Архімеда
Виштовхувальна сила. Закон Архімеда Физические свойства строительных материалов
Физические свойства строительных материалов Магнитное поле Земли
Магнитное поле Земли  Презентация по физике "Условие равновесия рычага. Правило моментов" - скачать
Презентация по физике "Условие равновесия рычага. Правило моментов" - скачать  Презентация по физике Как все двигается с точки зрения физики
Презентация по физике Как все двигается с точки зрения физики  Визначення опору навантаження лінії передачі методом еквівалентного перетину. (Лекция 15)
Визначення опору навантаження лінії передачі методом еквівалентного перетину. (Лекция 15) Технология компрессии изображений «Smart Compression of Images»
Технология компрессии изображений «Smart Compression of Images» Галогенная лампа
Галогенная лампа Виды спектров. Спектральный анализ.
Виды спектров. Спектральный анализ. Энергия. Кинетическая энергия
Энергия. Кинетическая энергия