Содержание
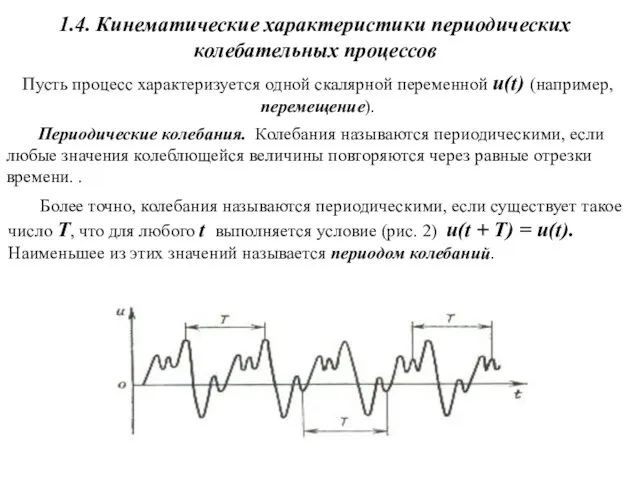
- 2. 1.4. Кинематические характеристики периодических колебательных процессов Периодические колебания. Колебания называются периодическими, если любые значения колеблющейся величины
- 3. В технике период колебаний обычно измеряется в секундах; частота f, следовательно, имеет размерность 1/с ( с
- 4. Гармонические колебания. Простейшим (и наиболее важным) видом периодических колебаний являются гармонические (синусоидальные) колебания, при которых колеблющаяся
- 5. Для этого на плоскости вводится вектор длиной А, который вращается с постоянной угловой скоростью, равной Проектируя
- 6. Скорость при гармонических колебаниях а ускорение Скорость v(t) и ускорение w(t) при гармонических колебаниях также изменяются
- 7. Сумма двух гармонических колебаний с одинаковыми частотами будет гармоническим колебанием с той же частотой: Амплитуда и
- 8. Полигармонические колебания. Полигармоническими называют колебания, которые могут быть представлены в виде суммы двух или более гармонических
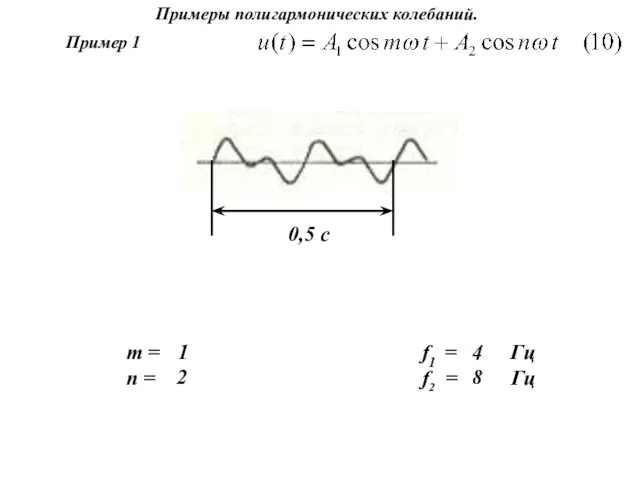
- 9. Примеры полигармонических колебаний. m = n = 1 0,5 c f1 = Гц f2 = Гц
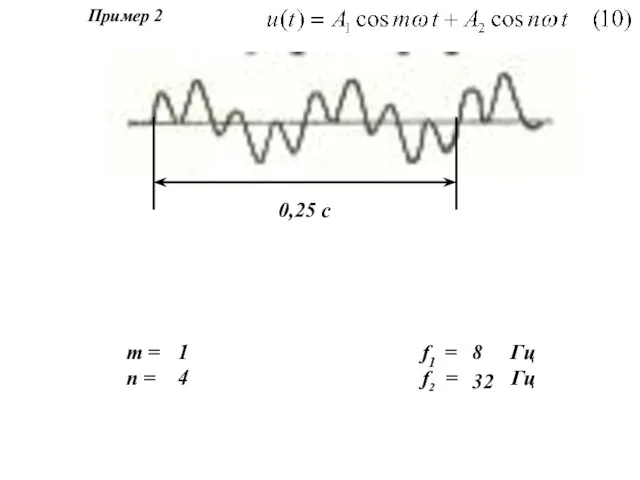
- 10. m = n = 1 0,25 c f1 = Гц f2 = Гц 8 Пример 2
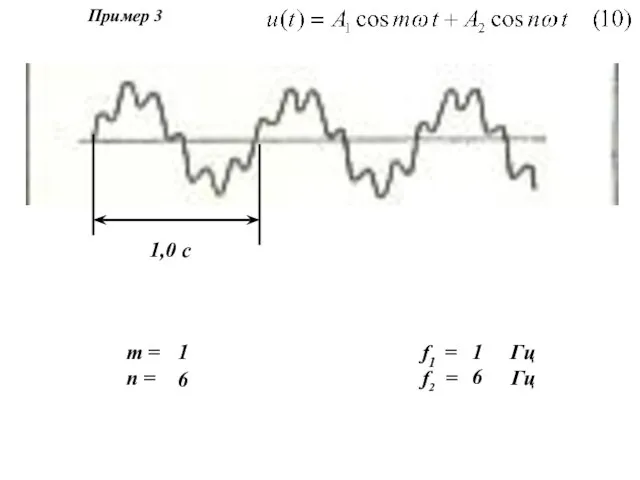
- 11. m = n = 1 1,0 c f1 = Гц f2 = Гц 1 Пример 3
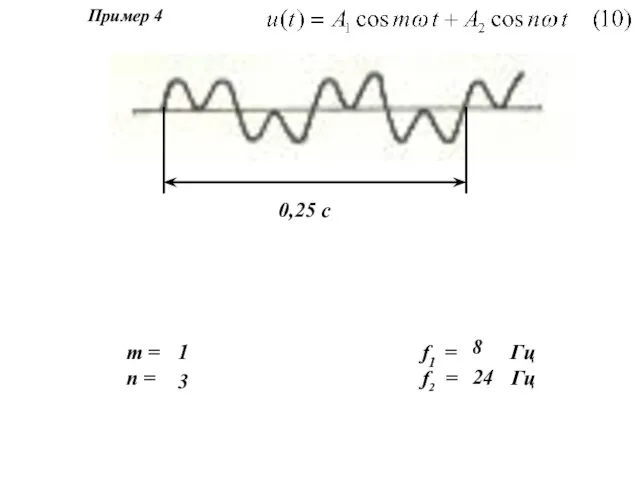
- 12. m = n = 1 0,25 c f1 = Гц f2 = Гц 8 Пример 4
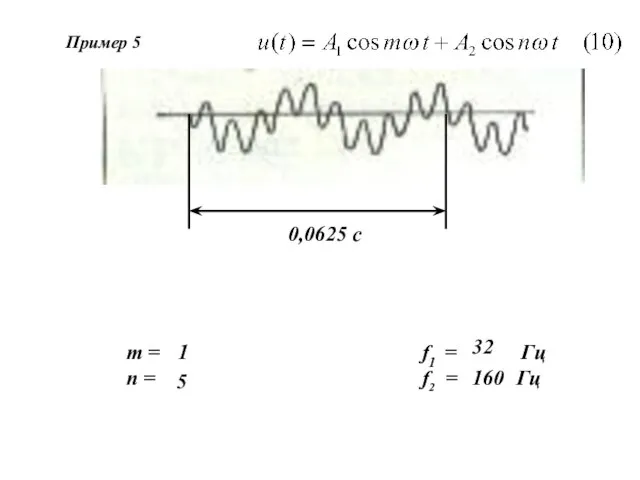
- 13. m = n = 1 0,0625 c f1 = Гц f2 = Гц 32 Пример 5
- 15. Скачать презентацию






 Презентация по физике "Электризация тел. Два рода электрических зарядов. Электрическое поле" -
Презентация по физике "Электризация тел. Два рода электрических зарядов. Электрическое поле" -  Электрический ток в полупроводниках
Электрический ток в полупроводниках Характеристика систем электроснабжения воздушных судов. Состав, назначение и классификация систем электроснабжения. (Тема 1.1)
Характеристика систем электроснабжения воздушных судов. Состав, назначение и классификация систем электроснабжения. (Тема 1.1) Презентация по физике "Сила Лоренца" - скачать
Презентация по физике "Сила Лоренца" - скачать  Плотность вещества
Плотность вещества Свойства водяного пара. Основные понятия и определения
Свойства водяного пара. Основные понятия и определения Параметры звукового поля
Параметры звукового поля Текстура рекристаллизации
Текстура рекристаллизации Элементы физической кинетики
Элементы физической кинетики Электромагнитные волны. Шкала электромагнитных волн
Электромагнитные волны. Шкала электромагнитных волн Топки. Пылеприготовление. Котельные установки
Топки. Пылеприготовление. Котельные установки Водяной пар в атмосфере
Водяной пар в атмосфере Тема:«Рентгеновское излучение» Работу выполнила ученица 11«А» класса МОУ «СОШ №95 им. Н. Щукина п.Архара» Гогулова Кристина Вал
Тема:«Рентгеновское излучение» Работу выполнила ученица 11«А» класса МОУ «СОШ №95 им. Н. Щукина п.Архара» Гогулова Кристина Вал Квазікласичне наближення для рівняння Дірака зі скалярно-векторним зв’язком кулонівського типу
Квазікласичне наближення для рівняння Дірака зі скалярно-векторним зв’язком кулонівського типу Интерференция волн
Интерференция волн Электромагнитные колебания
Электромагнитные колебания Ефект Доплера
Ефект Доплера Перемещение при прямолинейном равномерном движении
Перемещение при прямолинейном равномерном движении ОТКРЫТИЕ ЭЛЕКТРОМАГНИТНОЙ ИНДУКЦИИ (1831Г., М.ФАРАДЕЙ)
ОТКРЫТИЕ ЭЛЕКТРОМАГНИТНОЙ ИНДУКЦИИ (1831Г., М.ФАРАДЕЙ) Передающие среды
Передающие среды Конструкция двигателя НК-8-2У
Конструкция двигателя НК-8-2У Актуальные вопросы преподавания физики в 2019/2020 учебном году
Актуальные вопросы преподавания физики в 2019/2020 учебном году Твердотельные лазеры
Твердотельные лазеры Радиационный контроль
Радиационный контроль Аттестационная работа. Методическая разработка к проекту Выдающиеся ученые-физики
Аттестационная работа. Методическая разработка к проекту Выдающиеся ученые-физики Фотоэффект. Дискретное представление света
Фотоэффект. Дискретное представление света Електричні апарати. (Лекция 7)
Електричні апарати. (Лекция 7) Wind Energy Technology. (Lecture 8)
Wind Energy Technology. (Lecture 8)