Содержание
- 2. Температурное поле К числу основных задач теории теплообмена относится установление зависимости между тепловым потоком и распределением
- 3. Температурный градиент При любом температурном поле в теле всегда имеются точки с одинаковой температурой. Если соединить
- 4. Основной закон теплопроводности Условием передачи теплоты путём теплопроводности является наличие разности температур в различных точках тела.
- 5. Дифференциальное уравнение теплопроводности Из уравнения (1) распределение температуры можно определить только для тел простой конфигурации –
- 6. Теплопроводность плоской стенки при стационарном режиме Рассмотрим однородную стенку толщиной δ. Температура изменяется только в направлении
- 7. Теплопроводность плоской стенки при стационарном режиме Подставив значения C1 и C2 в уравнение (5), получим Расчётная
- 8. Теплопроводность цилиндрической стенки Рассмотрим однородную цилиндрическую стенку длиной l с внутренним диаметром d1 и внешним диаметром
- 10. Скачать презентацию
Температурное поле
К числу основных задач теории теплообмена относится установление зависимости между
Температурное поле
К числу основных задач теории теплообмена относится установление зависимости между
В наиболее общем случае температура в данной точке t зависит от координат точки (x, y, z) и изменяется во времени τ, т.е. температурное поле выражается функцией вида: t = f(x, y, z, τ) – уравнение неустановившегося (нестационарного) температурного поля.
Если температура тела есть функция только координат и не изменяется с течением времени, то температурное поле будет стационарным
t = f(x, y, z); dz/dτ = 0
Температура в теле может изменяться в направлении одной, двух и трёх координатных осей. В соответствии с этим температурное поле может быть одно-, двух- и трёхмерным.
Одномерной, например, является задача о переносе теплоты в стенке, у которой длина и ширина бесконечно велики по сравнению с толщиной. Для этого случая уравнение температурного поля для режима
нестационарного: t = f(x, τ); dt/dy = dt/dz = 0
стационарного: t = f(x); dz/dτ = 0 и dt/dy = dt/dz = 0
Температурный градиент
При любом температурном поле в теле всегда имеются точки с
Температурный градиент
При любом температурном поле в теле всегда имеются точки с
Пусть разность температур между двумя близлежащими изотермическими поверхностями составляет Δt. Кратчайшим расстоянием между этими поверхностями является расстояние по нормали Δn. При сближении указанных поверхностей отклонение Δt/Δn стремится к пределу
Производная температура по нормали к изотермической поверхности называется температурным градиентом. Этот градиент является вектором, направление которого соответствует повышению температуры. Перемещение тепла происходит по линии температурного градиента, но направлено в сторону, противоположную этому градиенту: q ~ (dt/dn)
Основной закон теплопроводности
Условием передачи теплоты путём теплопроводности является наличие разности температур
Основной закон теплопроводности
Условием передачи теплоты путём теплопроводности является наличие разности температур
dQ = - λ⋅dF⋅dτ⋅(dt/dn), Дж/ккал (1)
Знак минус показывает, что в направлении теплового потока температура убывает.
- коэффициент теплопроводности. Он характеризует собой способность вещества проводить тепло. Размерность λ находится из уравнения (1)
dQ dn Дж ⋅ м Вт
[λ] = [−−−−−−−] = [−−−−−−−−−−−] = [−−−−−−−],
df dτ dt м2 ⋅ с ⋅ град м⋅ град
При выражении Q в ккал/ч
ккал ккал Вт
[λ] = [−−−−−−−], причём 1 [−−−−−−−−] = 1,16 [−−−−−−],
м ⋅ ч ⋅ К м ⋅ ч ⋅ К м ⋅ К
Теплопроводность твёрдых тел является линейной функцией температуры: λ = λо(1 + bt),
где λ - теплопроводность при данной температуре, (t, oC), λo – теплопроводность при 0oC, b – const для данного материала. Для большинства жидкостей с увеличением температуры значение λ уменьшается (давление не влияет). Теплопроводность газов возрастает с повышением температуры и мало зависит от давления. Зависимость λ газов от температуры устанавливается формулой: λ = λо ⋅ (273 + С)\(Т + С) ⋅ (Т\273)3/2, где T – абсолютная температура, C – опытная const, λо – теплопроводность при 0oC
Дифференциальное уравнение теплопроводности
Из уравнения (1) распределение температуры можно определить только для
Дифференциальное уравнение теплопроводности
Из уравнения (1) распределение температуры можно определить только для
где а = λ/сρ, называется коэффициентом температуропроводности, м2/сек, равная отношению коэффициента теплопроводности к объёмной удельной теплоёмкости вещества и является мерой быстроты выравнивания температурного поля. Он характеризует теплоинерционные свойства тела: при прочих равных условиях быстрее нагревается или охлаждается то тело, которое обладает большим коэффициентом температуропроводности. Уравнение (2), описывающее пространственное и временное изменение температуры, относится к неустановившимся процессам теплопроводности. Для установившихся процессов dθ/dτ = 0, и уравнение теплопроводности принимает тогда более простой вид:
Уравнения (2) и (3) предполагают одновременное изменение температур тела по направлениям всех трёх осей координат, поэтому их часто называют уравнениями трёхмерных температурных полей.
(2)
(3)
Теплопроводность плоской стенки при стационарном режиме
Рассмотрим однородную стенку толщиной δ. Температура
Теплопроводность плоской стенки при стационарном режиме
Рассмотрим однородную стенку толщиной δ. Температура
При этих условиях количество теплоты, которое передаётся теплопроводностью через поверхность стенки f за время τ, согласно закону Фурье: dQ = - λ⋅dF⋅dτ⋅(dt/dn) (1)
На основании дифференциального уравнения теплопроводности распределение температур только вдоль оси x представится в виде:
Интегрирование этого уравнения приводит к функции t = C1x + C2 (5),
где C1 и C2 - константы интегрирования.
Уравнение (5) показывает, что по толщине плоской стенки температура изменяется прямолинейно. Константы интегрирования можно определить, приняв соответствующие граничные условия:
если х = 0, то t = tст1 и уравнение (5) примет вид: tст1 = C2
Если х = δ, то t = tст2 и tст2 = C1δ + C2 или tст2 = C1δ + tст1
откуда
(4)
Теплопроводность плоской стенки при стационарном режиме
Подставив значения C1 и C2 в
Теплопроводность плоской стенки при стационарном режиме
Подставив значения C1 и C2 в
Расчётная формула теплопроводности для установившегося теплового потока через многослойную плоскую стенку выводится из уравнения теплопроводности для отдельных слоёв. В общем виде уравнение имеет вид:
откуда
Подставив найденное значение температурного градиента в уравнение теплопроводности (1), получим
или
Теплопроводность цилиндрической стенки
Рассмотрим однородную цилиндрическую стенку длиной l с внутренним диаметром
Теплопроводность цилиндрической стенки
Рассмотрим однородную цилиндрическую стенку длиной l с внутренним диаметром
Обозначим:
Температура изменяется только в радиальном направлении. Выделим в стенке кольцевой слой с радиусом r и толщиной dr. Согласно закону Фурье, количество тепла, проходящего через такой слой, равно
Q = - λ⋅F⋅τ⋅(dt/dr) = - λ⋅2πrL⋅(dt/dr) (6)
Разделив переменные, получим
dt = - Q/(2πLλ) ⋅ dr/r (7)
Интегрируя уравнение (7) в пределах tст1 до tст2 и r1 и r2, получим
t1 - t2 = Q/(2πLλ) ⋅ lnr2/r1
Откуда
Q = 2πL (tст1 – tст2)/(1/λ ⋅ lnd2/d1) (8)
Выражение (8) является уравнением теплопроводности однородной цилиндрической стенки для установившегося теплового потока.







 Физика в маслёнке Выполнила: Васнева Анастасия Сергеевна Ученица 9 «В» класса ГОУ СОШ № 1338 САО Наставник и руководител
Физика в маслёнке Выполнила: Васнева Анастасия Сергеевна Ученица 9 «В» класса ГОУ СОШ № 1338 САО Наставник и руководител Cолнечная система
Cолнечная система Заготовительные операции ювелирного производства
Заготовительные операции ювелирного производства Полет в космос
Полет в космос Решение задач по теме «Законы Ньютона»
Решение задач по теме «Законы Ньютона» Коэффициент полезного действия (КПД) тепловых двигателей
Коэффициент полезного действия (КПД) тепловых двигателей Молекулярнокинетическая теория
Молекулярнокинетическая теория Броуновское движение. Силы взаимодействия молекул. Строение газообразных, жидких и твердых тел
Броуновское движение. Силы взаимодействия молекул. Строение газообразных, жидких и твердых тел Электричество и магнетизм (Лекция 10)
Электричество и магнетизм (Лекция 10) Дифференциальное уравнение теплопроводности
Дифференциальное уравнение теплопроводности Презентация Ломоносов-первый российский академик
Презентация Ломоносов-первый российский академик Элементы физической кинетики
Элементы физической кинетики Методы наблюдения и регистрации элементарных частиц
Методы наблюдения и регистрации элементарных частиц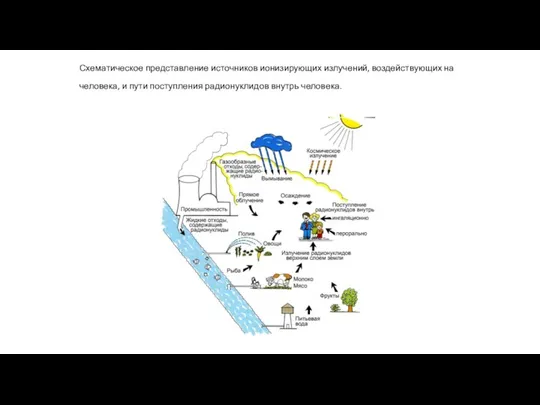 Схематическое представление источников ионизирующих излучений, воздействующих на человека
Схематическое представление источников ионизирующих излучений, воздействующих на человека Температура и термометры
Температура и термометры Основные положения спектроскопии
Основные положения спектроскопии History of welding
History of welding Работа и мощность
Работа и мощность Строение атома. Опыт Резерфорда
Строение атома. Опыт Резерфорда Дифузія в побуті
Дифузія в побуті Жас физик
Жас физик Нанотехнологии и наночастицы. Новые факторы в гигиене труда
Нанотехнологии и наночастицы. Новые факторы в гигиене труда Презентация по физике "Строение атома ( АZX )" - скачать
Презентация по физике "Строение атома ( АZX )" - скачать  Червячные передачи
Червячные передачи Основные сведения о переходном процессе в электроэнергетике в электрической дуге
Основные сведения о переходном процессе в электроэнергетике в электрической дуге Потенциальная энергия
Потенциальная энергия Презентация по физике "Спектры и спектральный анализ" - скачать
Презентация по физике "Спектры и спектральный анализ" - скачать  Радиоактивность. Открытие радиоактивности. Природа радиоактивных излучений. Радиоактивные превращения. Изотопы
Радиоактивность. Открытие радиоактивности. Природа радиоактивных излучений. Радиоактивные превращения. Изотопы