Содержание
- 2. Прямая задача кинематики криволинейного движения. Критерии: угол поворота, угловая скорость, угловое ускорение. Обратная задача кинематики криволинейного
- 3. Движение по окружности и его кинематические характеристики. Описание движения по окружности. Для начала рассмотрим один из
- 4. Движение частицы по окружности в декартовой системе координат.
- 5. Угловые кинематические характеристики. Рассмотрим движение частицы в плоскости XY в полярных координатах: ρ = const, φ
- 6. Вектор угловой скорости и ускорения. То, что величина элементарного углового перемещения действительно является вектором, можно доказать,
- 7. Вектор углового ускорения вводится по аналогии с поступательным движением, т.е. как производная от угловой скорости по
- 8. Криволинейное движение. Нормальное и тангенциальное ускорения. Нормальное ускорение. Поскольку вектор ускорения при криволинейном движении сориентирован по
- 10. Скачать презентацию







 Інфразвук. Джерела інфразвуку
Інфразвук. Джерела інфразвуку Электромобиль – экологически чистое транспортное средство
Электромобиль – экологически чистое транспортное средство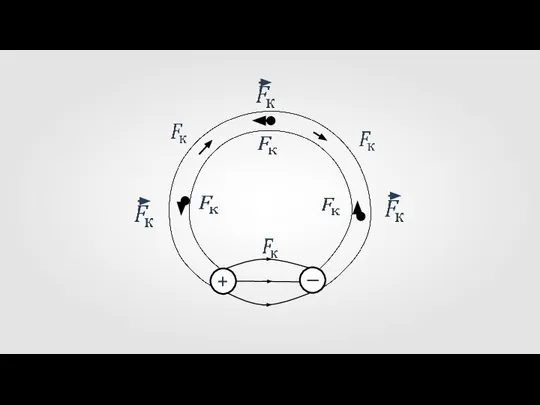 Cторонние силы
Cторонние силы Эрнест Резерфорд
Эрнест Резерфорд МОБІЛЬНИЙ ЗВ’ЯЗОК Основні поняття Статистичні дані Принцип дії Вплив випромінювання Ситуація в Україні
МОБІЛЬНИЙ ЗВ’ЯЗОК Основні поняття Статистичні дані Принцип дії Вплив випромінювання Ситуація в Україні  Тормозные жидкости автомобилей
Тормозные жидкости автомобилей История фотоаппарата
История фотоаппарата Плюсы солнечных батарей
Плюсы солнечных батарей Природа и эволюция звезд
Природа и эволюция звезд Основы гидравлики
Основы гидравлики Izoparametriski procesi
Izoparametriski procesi Моделирование электростатического поля
Моделирование электростатического поля Техническая термодинамика. Циклы энергетических установок. (Лекция 7)
Техническая термодинамика. Циклы энергетических установок. (Лекция 7) Вечный двигатель Китавнин Андрей, 10 «Б» класс
Вечный двигатель Китавнин Андрей, 10 «Б» класс Сила
Сила Электроскоп. Назначение. Принцип действия
Электроскоп. Назначение. Принцип действия Применение термолюминесцентной дозиметрии для измерение полей рентгеновского излучения
Применение термолюминесцентной дозиметрии для измерение полей рентгеновского излучения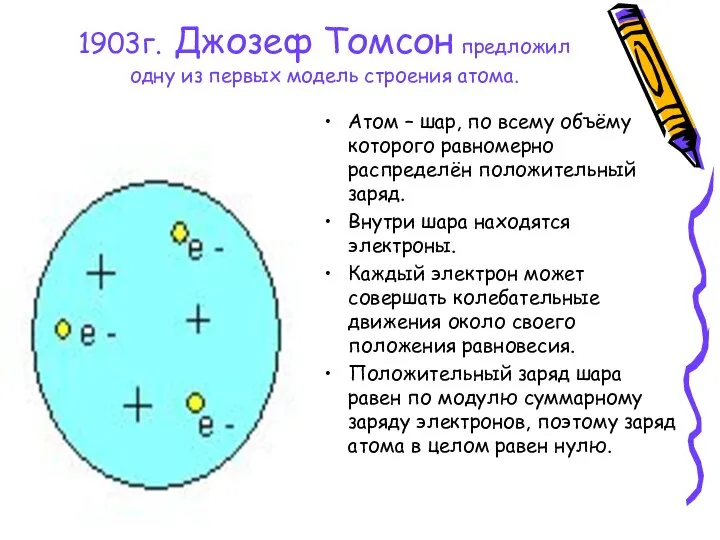 1903г. Джозеф Томсон предложил одну из первых модель строения атома.
1903г. Джозеф Томсон предложил одну из первых модель строения атома.  Презентация по физике "КВАНТОВІ ГЕНЕРАТОРИ. ПРИНЦИП ДІЇ ТА ЗАСТОСУВАННЯ" - скачать
Презентация по физике "КВАНТОВІ ГЕНЕРАТОРИ. ПРИНЦИП ДІЇ ТА ЗАСТОСУВАННЯ" - скачать 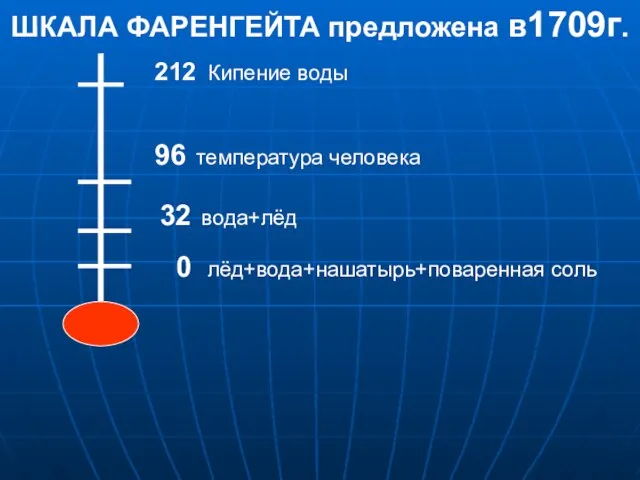 Презентация по физике "Шкала Фаренгейта предложена в 1709г" - скачать
Презентация по физике "Шкала Фаренгейта предложена в 1709г" - скачать  Магниторазведка
Магниторазведка Масса тел
Масса тел Резонанс у медицині Підготувала Учениця 11 класу Герасименко Анастасія
Резонанс у медицині Підготувала Учениця 11 класу Герасименко Анастасія  Аўтаматызацыя вымярэнняў і дыстанцыйнае кіраванне тэхналагічнымі аб’ектамі нафтаправоднага транспарту
Аўтаматызацыя вымярэнняў і дыстанцыйнае кіраванне тэхналагічнымі аб’ектамі нафтаправоднага транспарту Электрические свойства биоткани на переменном токе
Электрические свойства биоткани на переменном токе Презентация Давление. Гидравлический пресс
Презентация Давление. Гидравлический пресс  Презентация по физике "Архимедова сила и плавание тел" - скачать
Презентация по физике "Архимедова сила и плавание тел" - скачать  Проверочная работа по теме «Электрический ток»
Проверочная работа по теме «Электрический ток»