Содержание
- 2. Лекция 7 Плоское потенциальное движение
- 3. Применение функций комплексного переменного Как уже отмечали, для для плоских потенци-альных течений существуют функции, связан-ные соотношениями
- 4. Применение функций комплексного переменного В теории функций комплексного переменного доказывается, что если две функции φ(х,у) и
- 5. Применение функций комплексного переменного х Re z Im z у r z = x + iy
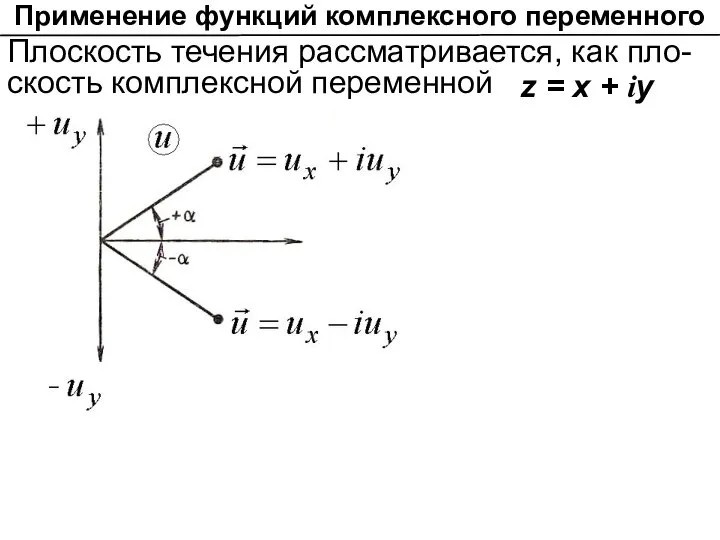
- 6. Применение функций комплексного переменного Плоскость течения рассматривается, как пло-скость комплексной переменной z = x + iy
- 7. Комплексное число также можно изображать радиус-вектором. Длина радиус-вектора, изоб- ражающего комплексное число , называется модулем комплексного
- 8. Применение функций комплексного переменного О комплексных числах Модуль любого ненулевого комплексного чис- ла есть положительное число.
- 9. Модуль произведения (частного) двух комп- лексных чисел равен произведению (частно- му) модулей каждого из чисел. Применение
- 10. Применение функций комплексного переменного Тригонометрической формой комплексного числа называется выражение Показательной формой комплексного числа называется выражение
- 11. Для того, чтобы функция w (z)= φ +iψ=φ(x,y)+iψ(x,y), определенная в некоторой области, была дифференцируемой в точке
- 12. Применение функций комплексного переменного Такая функция называется аналитической. Следовательно, любую аналитическую функ-цию w(z) можно рассматривать как
- 13. Применение функций комплексного переменного
- 14. действительная часть которой равна проекции скорости иx, а мнимая – взятой с обратным знаком проекции иу
- 15. Применение функций комплексного переменного При сложении течений комплексные потенци- алы суммируются: W(z) = W1(z) + W2(z)
- 16. Применение функций комплексного переменного В плоскости течения могут находиться точки, в которых производная комплексного потенци-ала обращается
- 17. (и =0) пересекаются две или несколько (конеч-ное число) линий тока. Эти точки называются точками разветвления, а
- 18. Применение функций комплексного переменного Величину называют сопряженной скopо-стью. В комплексной плоскости иx, иу называ-емой плоскостью годографа
- 19. Во-вторых, можно, задавшись аналитической функцией W, выделить в ней действительную и мнимую части (т. е. φ
- 20. Рассмотрим, как выразится комплексный потенциал для элементарных потоков.
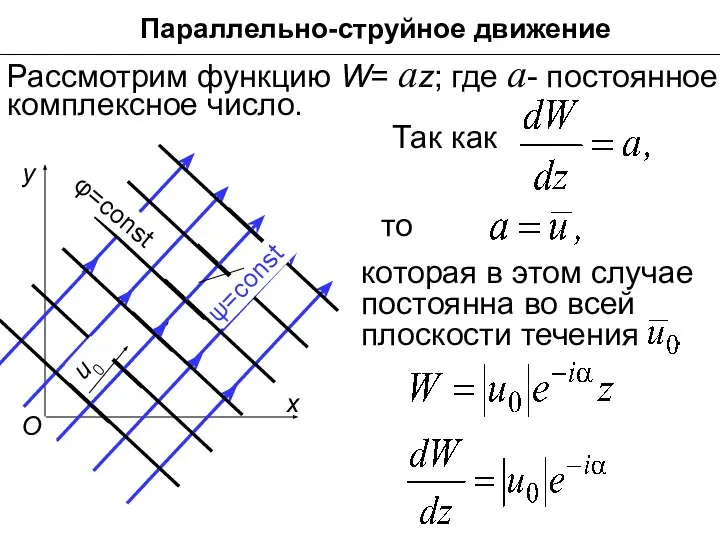
- 21. Параллельно-струйное движение Рассмотрим функцию W= az; где а- постоянное комплексное число. Так как то которая в
- 22. Параллельно-струйное движение Вдоль линий тока ψ= const и, следовательно, их уравнение запишется, в виде Это уравнение
- 23. Параллельно-струйное движение Эквипотенциали представляют собой дpyгoе семейство параллельных прямых, ортогональ-ное к первому.
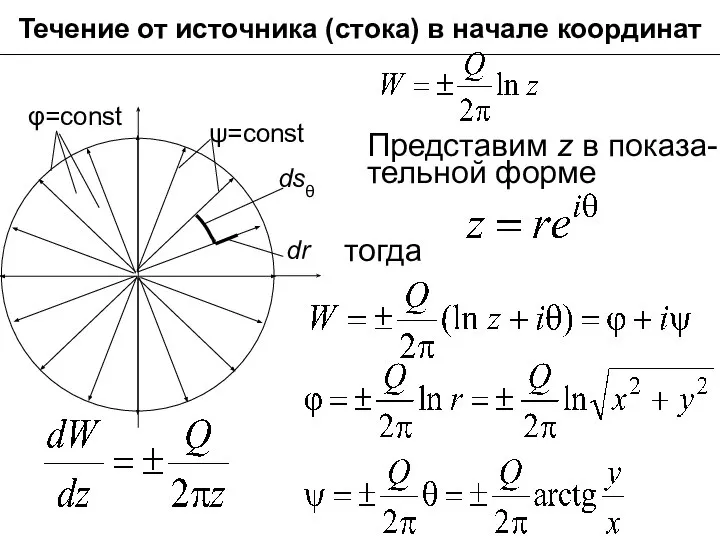
- 24. Течение от источника (стока) в начале координат dsθ Представим z в показа-тельной форме тогда
- 25. Течение от источника (стока) в начале координат Линии тока (ψ= cоnst или у/х =const) представ-ляют собой
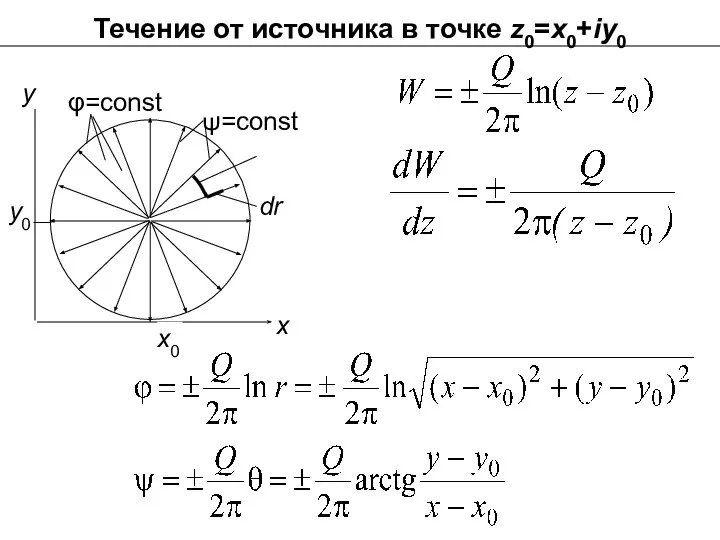
- 26. Течение от источника в точке z0=x0+iy0 ψ=const dr φ=const x x0 y0 y
- 27. Течение от вихря в точке z0=x0+iy0 y0 x x0 y0 y
- 29. Скачать презентацию






















 Властивості рідин. Поверхневий натяг. Змочування
Властивості рідин. Поверхневий натяг. Змочування Дифференциальное уравнение энергии трехмерной нестационарной теплопроводности твердых тел
Дифференциальное уравнение энергии трехмерной нестационарной теплопроводности твердых тел Упругое рассеяние в центральном поле
Упругое рассеяние в центральном поле Кинематика. Решение задач
Кинематика. Решение задач Физики, именами которых названы единицы измерения
Физики, именами которых названы единицы измерения Густина речовини. Одиниці густини
Густина речовини. Одиниці густини Современная система дозиметрических величин
Современная система дозиметрических величин Сила. Явление тяготения. Сила тяжести
Сила. Явление тяготения. Сила тяжести Радиоспектроскопические методы исследования, часть 1
Радиоспектроскопические методы исследования, часть 1 Применение фотоэффекта
Применение фотоэффекта Первый этап в развитии физики элементарных частиц. От электрона до позитрона: 1897-1932
Первый этап в развитии физики элементарных частиц. От электрона до позитрона: 1897-1932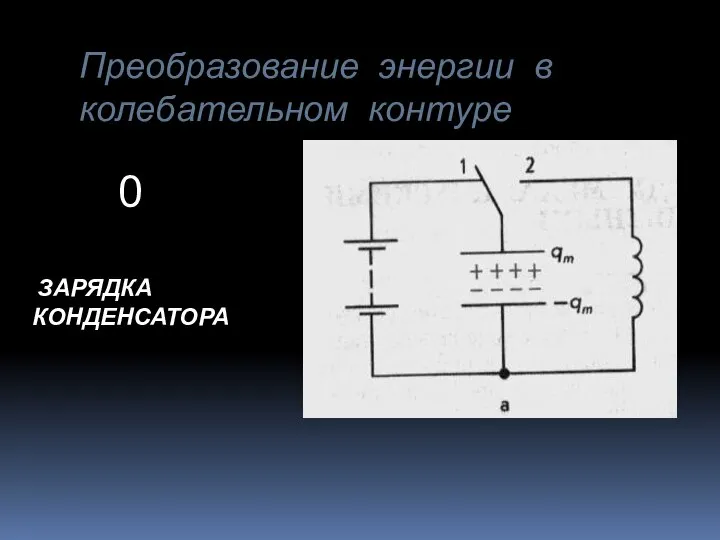 Преобразование энергии в колебательном контуре
Преобразование энергии в колебательном контуре  Диэлектриктердегі электр өрісі үшін
Диэлектриктердегі электр өрісі үшін Физика 10 класс 1 урок в разделе «Молекулярная физика»
Физика 10 класс 1 урок в разделе «Молекулярная физика» «Производство и использование электрической энергии»
«Производство и использование электрической энергии»  Презентация по физике "Работа теплового двигателя" - скачать
Презентация по физике "Работа теплового двигателя" - скачать  Физические величины. Измерение физических величин. Точность и погрешность измерений
Физические величины. Измерение физических величин. Точность и погрешность измерений Электростатическое поле в проводниках. Тема 4
Электростатическое поле в проводниках. Тема 4 Презентация по физике "Механические колебания (11 класс)" - скачать бесплатно
Презентация по физике "Механические колебания (11 класс)" - скачать бесплатно Основы динамики. Три закона Ньютона
Основы динамики. Три закона Ньютона Агрегатные состояния вещества. Строение твердых, жидких и газообразных тел (в стихах)
Агрегатные состояния вещества. Строение твердых, жидких и газообразных тел (в стихах) Буландыру. Буландыру әдістері
Буландыру. Буландыру әдістері Частные случаи движения точки
Частные случаи движения точки Разработка подвески багги
Разработка подвески багги Роль фізики в екологічній освіті
Роль фізики в екологічній освіті Уравнение газового состояния. Решение задач
Уравнение газового состояния. Решение задач Гироскопы МЭМС
Гироскопы МЭМС Термомеханический эффект
Термомеханический эффект