Содержание
- 2. § 1. Классификация связей Связями называются любого вида ограничения, которые накладываются на положения и скорости точек
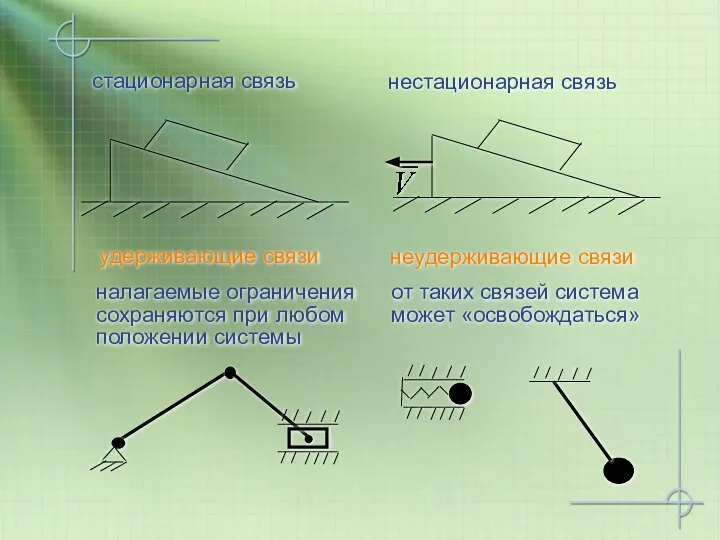
- 3. удерживающие связи налагаемые ограничения сохраняются при любом положении системы стационарная связь нестационарная связь неудерживающие связи от
- 4. § 2. Возможные перемещения системы Влияние связей Появление сил реакции Перемещения, которые могут иметь точки системы
- 5. Возможные перемещения характеризуются тем, что могут и не происходить (воображаемые) бесконечно малые происходят с сохранением всех
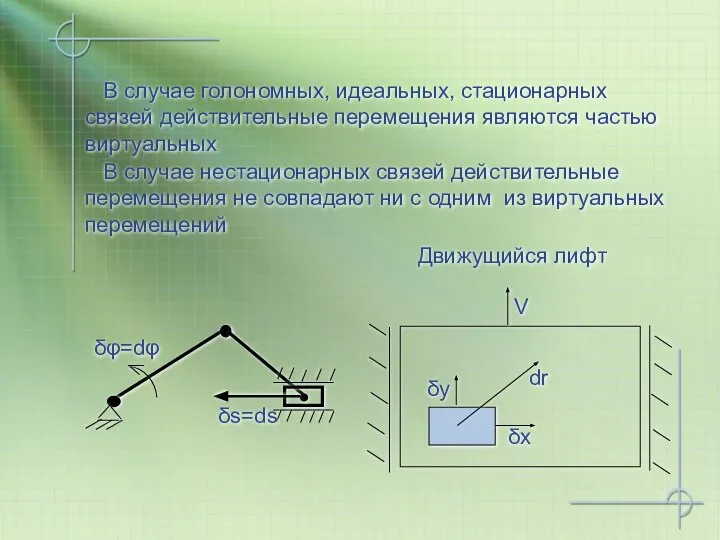
- 6. В случае нестационарных связей действительные перемещения не совпадают ни с одним из виртуальных перемещений В случае
- 7. Механическая система одновременно может иметь несколько возможных перемещений Число независимых между собой возможных перемещений механической системы
- 9. Выполняется в инерциальных системах отсчета Устанавливает общее условие равновесия механической системы в целом Все точки системы
- 10. Все связи будем считать стационарными Связь называется идеальной, если работа реакций этих связей на любых возможных
- 11. Андре-Мари Ампер (фр. Andre Marie Ampere; 22 января 1775 — 10 июня 1836) — знаменитый французский
- 12. Принцип возможных перемещений (ПВП) первым без доказательства сформулировал Иоганн Бернулли Иоганн Бернулли (нем. Johann Bernoulli, 27
- 13. Принцип возможных перемещений (ПВП) Для удерживающих связей Для освобождающихся связей Первым доказал и сформулировал в общем
- 14. Жозеф Луи Лагранж (фр. Joseph Louis Lagrange 25 января 1736, Турин – 10 апреля 1813, Париж)
- 15. Михаил Васильевич Остроградский (12(24) сентября 1801−20 декабря 1861(1 января 1862) − российский и украинский математик и
- 16. − уравнение возможных работ Уравнение возможных работ в аналитической форме Для равновесия механической системы с идеальными
- 17. Необходимость: Пусть механическая система находится под действием внешних сил, главный вектор которых Тогда для каждой точки
- 18. Достаточность: Пусть механическая система с идеальными связями, удовлетворяющая неравенству При стационарных связях действительные перемещения совпадают с
- 19. Если не все связи, наложенные на систему, являются идеальными, например, негладкие опорные поверхности, то к задаваемым
- 20. § 4. Решение задач с помощью ПВП а) определяют степени свободы Для этого останавливают поступательное или
- 21. План решения геометрическим способом в случае, когда система обладает одной степенью свободы 1. Изобразить все активные
- 22. 3. Задать возможное перемещение одной из точек системы (δφk или δsk) и выразить возможные перемещения точек
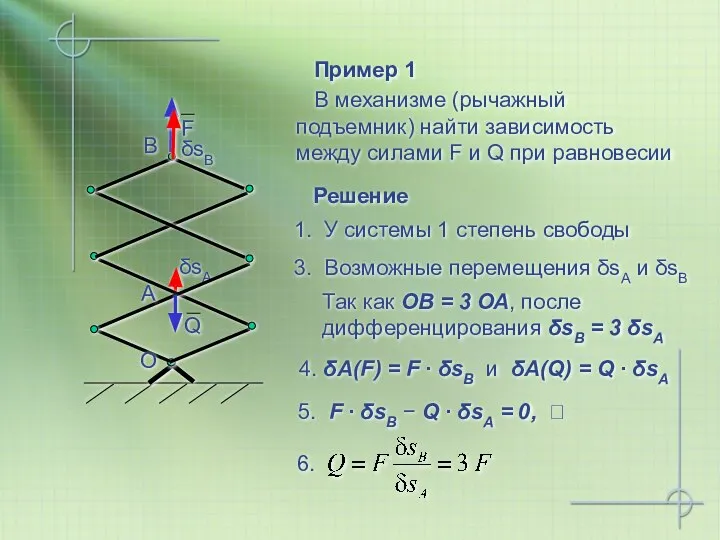
- 23. Пример 1 В механизме (рычажный подъемник) найти зависимость между силами F и Q при равновесии О
- 24. α Пример 2 Вес бревна Q, вес каждого из двух цилиндрических катков, на которые оно положено,
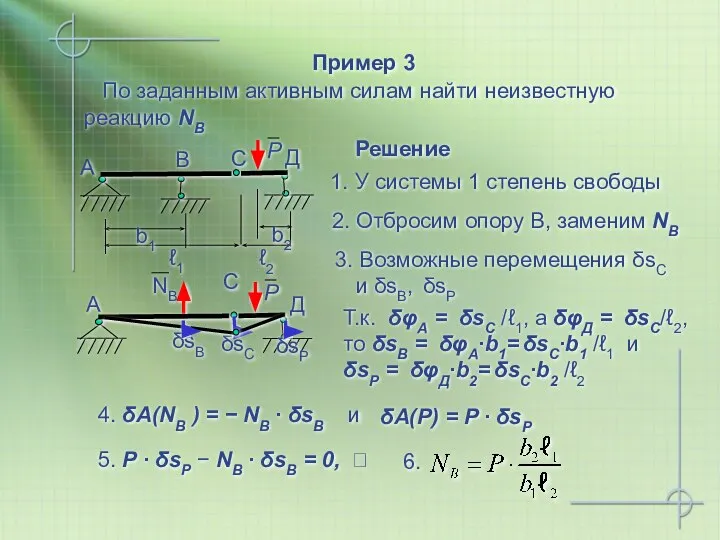
- 25. Пример 3 По заданным активным силам найти неизвестную реакцию NВ 1. У системы 1 степень свободы
- 26. Применяя одновременно п-п Даламбера и ПВП, можно определить общий метод решения задач динамики Рассмотрим систему материальных
- 27. Получим п-п Даламбера-Лагранжа При движении механической системы с идеальными связями в каждый момент времени сумма элементарных
- 28. Жа́н Леро́н Д’Аламбе́р (фр. Jean Le Rond d'Alembert; 16 ноября 1717 – 29 октября 1783) –
- 29. Пример Если система состоит из нескольких твердых тел, то к действующим на каждое тело силам нужно
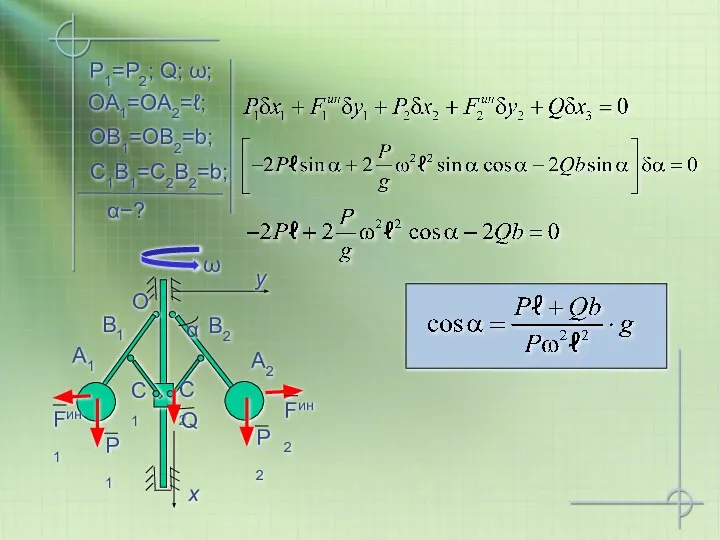
- 30. Р1=Р2; Q; ω; При определенном соотношении сил наступает равновесие ОА1=ОА2=ℓ; ОВ1=ОВ2=b; C1В1=C2В2=b; α−? Продифференцируем координаты
- 31. Р1=Р2; Q; ω; ОА1=ОА2=ℓ; ОВ1=ОВ2=b; C1В1=C2В2=b; α−?
- 32. Пример 2 Определить ускорение груза подъемника при постоянном вращающем моменте М Р1, Р2, Q, М r1,
- 34. Скачать презентацию

























 Изотопная геология (введение)
Изотопная геология (введение) Диэлектрические потери
Диэлектрические потери Импульс, энергия, законы сохранения. Решение задач
Импульс, энергия, законы сохранения. Решение задач Классификация методов синтеза наноматериалов
Классификация методов синтеза наноматериалов Презентація з фізичного практикуму на тему:”Фізика й науково-технічний прогрес” підготувала: учениця 11-А класу Харківської ЗОШ І-ІІІ ст №102 Антіпова Марія
Презентація з фізичного практикуму на тему:”Фізика й науково-технічний прогрес” підготувала: учениця 11-А класу Харківської ЗОШ І-ІІІ ст №102 Антіпова Марія  Презентация по физике "Напряжение" - скачать
Презентация по физике "Напряжение" - скачать  Зубчатые передачи
Зубчатые передачи Нагревание проводников электрическим током. Закон Джоуля-Ленца
Нагревание проводников электрическим током. Закон Джоуля-Ленца Штормгласс - предсказатель бурь
Штормгласс - предсказатель бурь Передача и использование электроэнергии
Передача и использование электроэнергии Электрическое поле. (лекция 1а)
Электрическое поле. (лекция 1а) Механическое движение и его виды
Механическое движение и его виды Действие магнитного поля на проводник с током. Электрический двигатель
Действие магнитного поля на проводник с током. Электрический двигатель Физические основы термодинамики
Физические основы термодинамики Теплопроводность при наличии внутренних источников теплоты
Теплопроводность при наличии внутренних источников теплоты Ультразвук и инфразвук в природе
Ультразвук и инфразвук в природе Вес воздуха. Атмосферное давление. Выполнил: студент 4 курса Специальность физика Д.Е. Таргоний
Вес воздуха. Атмосферное давление. Выполнил: студент 4 курса Специальность физика Д.Е. Таргоний Движение под действием нескольких сил
Движение под действием нескольких сил Современные проблемы технической физики. Самые дорогие научные проекты
Современные проблемы технической физики. Самые дорогие научные проекты Макс Карл Эрнст Людвиг Планк (23.05.1858-04.10.1947)
Макс Карл Эрнст Людвиг Планк (23.05.1858-04.10.1947) Лабораторные работы по физике 8 класс
Лабораторные работы по физике 8 класс Принципы радиосвязи. (8 класс)
Принципы радиосвязи. (8 класс) Индикаторлық галоидты жанарғы
Индикаторлық галоидты жанарғы Электрическое поле
Электрическое поле ПРОЕКТ «Определение средней скорости моего движения.» Выполнил ученик 7Б класса
ПРОЕКТ «Определение средней скорости моего движения.» Выполнил ученик 7Б класса  Светодиодные лампы
Светодиодные лампы Внутренняя энергия. Термодинамика
Внутренняя энергия. Термодинамика Термодинамика поверхностных явлений. (Часть 2)
Термодинамика поверхностных явлений. (Часть 2)