Содержание
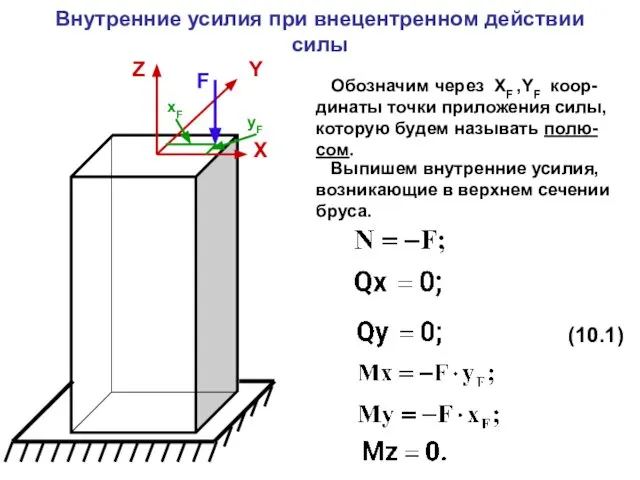
- 2. Внутренние усилия при внецентренном действии силы Обозначим через XF ,YF коор-динаты точки приложения силы, которую будем
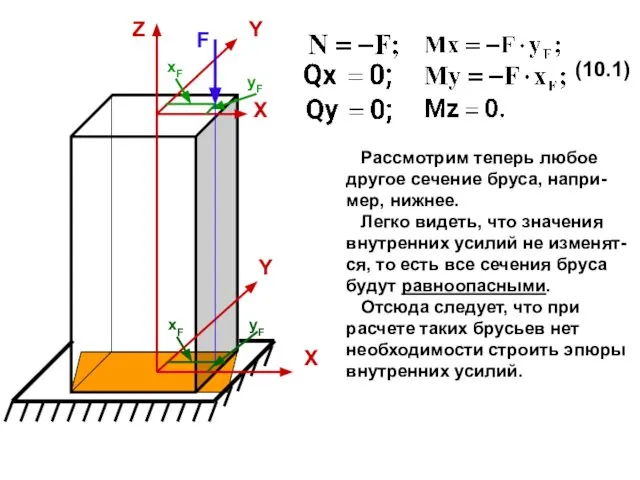
- 3. xF yF Рассмотрим теперь любое другое сечение бруса, напри-мер, нижнее. Легко видеть, что значения внутренних усилий
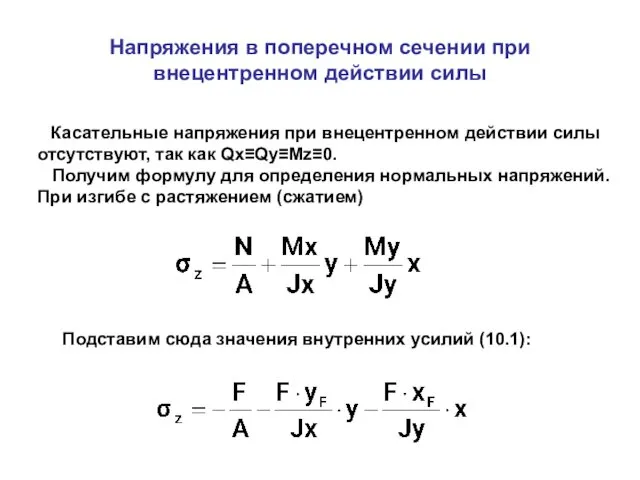
- 4. Напряжения в поперечном сечении при внецентренном действии силы Касательные напряжения при внецентренном действии силы отсутствуют, так
- 5. Вынесем за скобку величину Теперь учтем, что , а также случай действия растягивающей силы, при которой
- 6. В формуле (10.2) xF ,yF -координаты точки приложения силы (полюса); x,y -координаты точки, в которой определяются
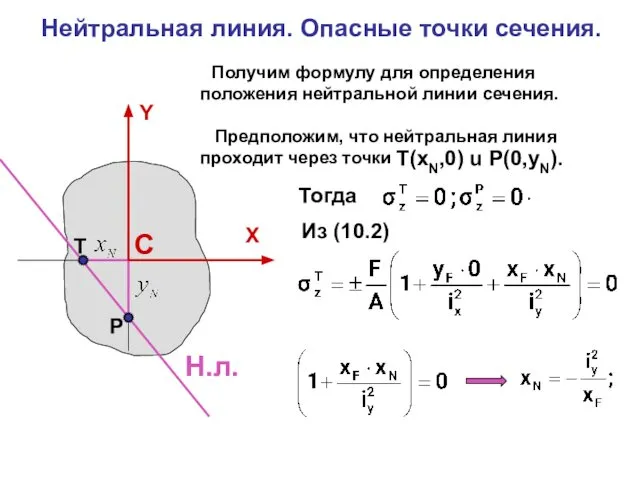
- 7. Нейтральная линия. Опасные точки сечения. Н.л. С Тогда Из (10.2) Р T Получим формулу для определения
- 8. (10.3) Аналогично из условия получим Таким образом, получены формулы для определения положения нейтральной линии:
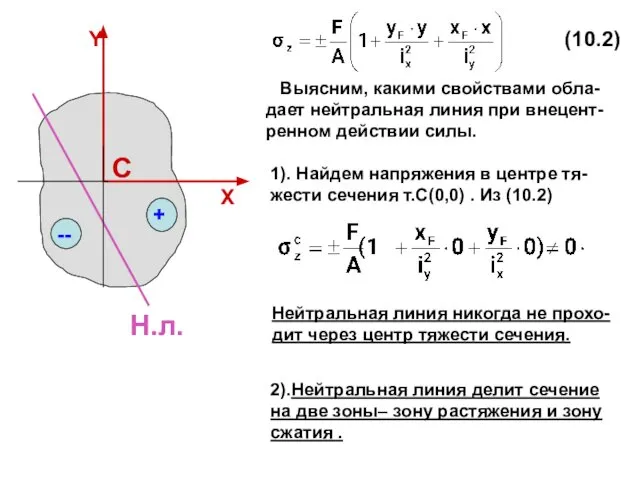
- 9. 1). Найдем напряжения в центре тя-жести сечения т.С(0,0) . Из (10.2) Нейтральная линия никогда не прохо-дит
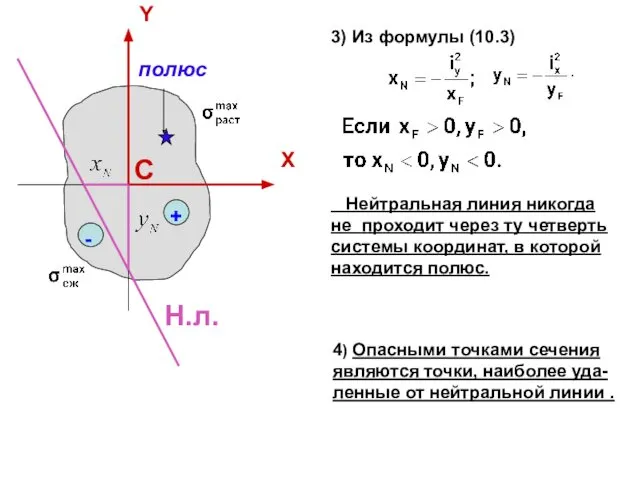
- 10. Н.л. С 3) Из формулы (10.3) 4) Опасными точками сечения являются точки, наиболее уда-ленные от нейтральной
- 11. С 5) Предположим, что полюс лежит на одной из осей координат, напри-мер, на оси Х. Тогда
- 12. Ядро сечения Внецентренное действие силы часто возникает в стойках, колоннах, выполненных из хрупких материалов– бетон, камень,
- 13. Внецентренное сжатие или если точка приложе-ния силы находится в осо-бой области сечения, на-зываемой ядром сечения .
- 14. При некотором положении полюса нейтральная линия коснется границы сечения . Н.л полюс Ядро сечения Н.л Ядро
- 15. Н.Л. Н.Л.
- 16. Это обстоятельство мож-но использовать при опре-делении положения ядра сечения. Рассмотрим, на-пример, прямоугольное се-чение . Предположим, что
- 17. 3 1 2 h b У1 А В Отсюда Из (10.2) : Аналогично можно найти коор-
- 18. 1 2 А В К Это уравнение прямой линии. 4 3 Покажем, что при повороте нейтральной
- 20. Скачать презентацию











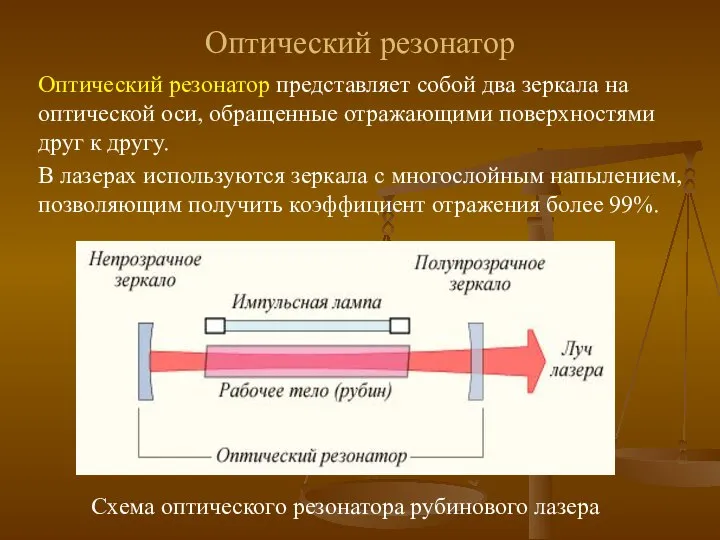 Оптический резонатор
Оптический резонатор Светодиодные лампы
Светодиодные лампы Основные положения корпускулярной теории Ньютона
Основные положения корпускулярной теории Ньютона Первое начало термодинамики. Внутренняя энергия. Работа и теплота. Теплоемкость идеального газа. (Лекция 7)
Первое начало термодинамики. Внутренняя энергия. Работа и теплота. Теплоемкость идеального газа. (Лекция 7) Презентация по физике "Различные магниты" - скачать
Презентация по физике "Различные магниты" - скачать  Стакан чая и физика
Стакан чая и физика Виконала Учениця 11-А класу Кіронда Яна
Виконала Учениця 11-А класу Кіронда Яна  Проверка закона Ома для участка цепи. Виды соединений
Проверка закона Ома для участка цепи. Виды соединений Гидравлический удар
Гидравлический удар Жылутехникасы жјне термодинамика
Жылутехникасы жјне термодинамика Применение кристаллов в науке и технике
Применение кристаллов в науке и технике Спектры и спектральные закономерности. Спектры электромагнитного излучения
Спектры и спектральные закономерности. Спектры электромагнитного излучения Презентация по физике "Изопроцессы" - скачать
Презентация по физике "Изопроцессы" - скачать  Схемы электрических соединений на стороне 6-10 кВ. (Лекция 12)
Схемы электрических соединений на стороне 6-10 кВ. (Лекция 12) Процессы, происходящие в веществе при его бомбардировке электронами
Процессы, происходящие в веществе при его бомбардировке электронами Проект урока подготовила: учитель I категории: Харькова И.В. Решение задач по теме: «Статика».
Проект урока подготовила: учитель I категории: Харькова И.В. Решение задач по теме: «Статика». Свойства канонического ансамбля. Поступательная сумма и интеграл по состояниям. Формула Закура-Тетроде. Лекция 20
Свойства канонического ансамбля. Поступательная сумма и интеграл по состояниям. Формула Закура-Тетроде. Лекция 20 Энергияның негізгі көздері, электрстанцияларының сипаттамасы
Энергияның негізгі көздері, электрстанцияларының сипаттамасы Атомная физика. Корпускулярно-волновой дуализм свойств материи. Гипотеза Луи де Бройля. Формула де Бройля
Атомная физика. Корпускулярно-волновой дуализм свойств материи. Гипотеза Луи де Бройля. Формула де Бройля Оптические приборы
Оптические приборы Ядерные технологии
Ядерные технологии Самые крутые подвесные дороги мира. Как работает канатная дорога?
Самые крутые подвесные дороги мира. Как работает канатная дорога? Механическое движение
Механическое движение Презентация по физике "Звуковые волны" - скачать бесплатно
Презентация по физике "Звуковые волны" - скачать бесплатно Услуги спецтехники. Компания RSG
Услуги спецтехники. Компания RSG Сила тока. Повторение
Сила тока. Повторение Электрические цепи переменного тока
Электрические цепи переменного тока Соединение деталей из тонколистового металла
Соединение деталей из тонколистового металла