Содержание
- 2. Угловой момент Движение в центральном поле. Атом водорода: волновые функции и уровни энергии Вопрос 7
- 3. Угловой момент Собственные значения операторов квадрата и проекции момента импульса, квадрата орбитального момента и проекции орбитального
- 4. Сферические гармоники и полиномы Лежандра: пример расчета в Maple
- 5. Сферические гармоники и присоединенные функции Лежандра
- 6. Сферические гармоники и гипергеометрическая функция
- 7. Сферические гармоники: пример расчета в Maple
- 8. Движение в центральном поле для атома Н
- 9. Атом водорода: уровни энергии и спектр излучения Hα Hβ Спектры излучения атомов H, Hg и молекулы
- 10. Атом водорода: спектральные серии, уровни энергии и волновые функции l − орбитальное квантовое число n −
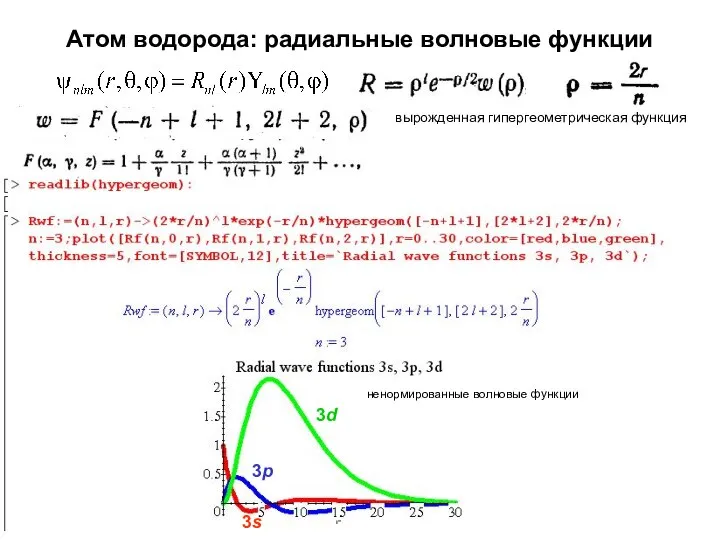
- 11. Атом водорода: радиальные волновые функции вырожденная гипергеометрическая функция ненормированная волновая функция
- 12. Атом водорода: радиальные волновые функции вырожденная гипергеометрическая функция 3s 3d 3p ненормированные волновые функции
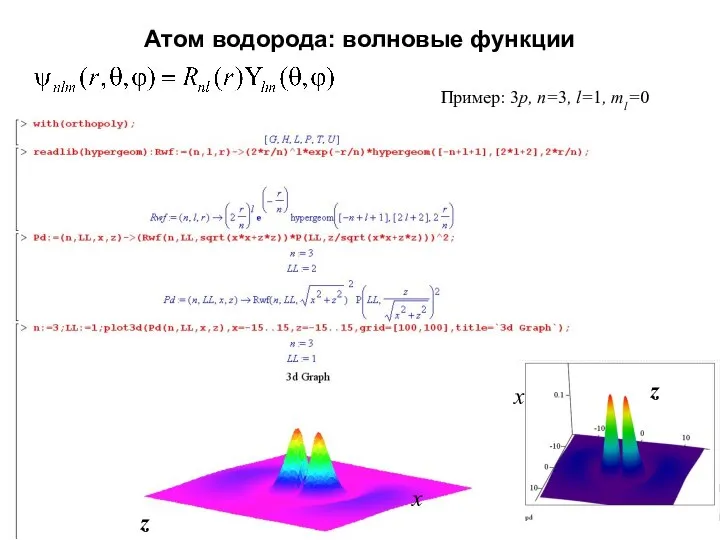
- 13. Атом водорода: волновые функции Пример: 3p, n=3, l=1, ml=0 z x x z
- 14. Вопрос 8. Теория упругого рассеяния: дифференциальное сечение рассеяния, волновая функция и амплитуда рассеяния Борновское приближение. Парциальное
- 15. Дифференциальное сечение рассеяния Основным источником сведений о распределении электрического заряда в атомном ядре явилось исследование рассеяния
- 16. Волновая функция ψ и амплитуда рассеяния f(θ) z Плотность потока вдоль оси z Плоская волна расходящаяся
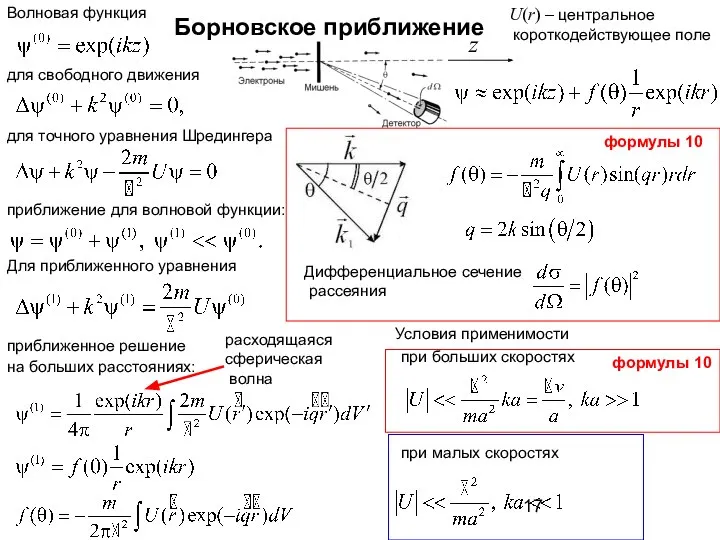
- 17. Борновское приближение для точного уравнения Шредингера для свободного движения приближенное решение на больших расстояниях: Условия применимости
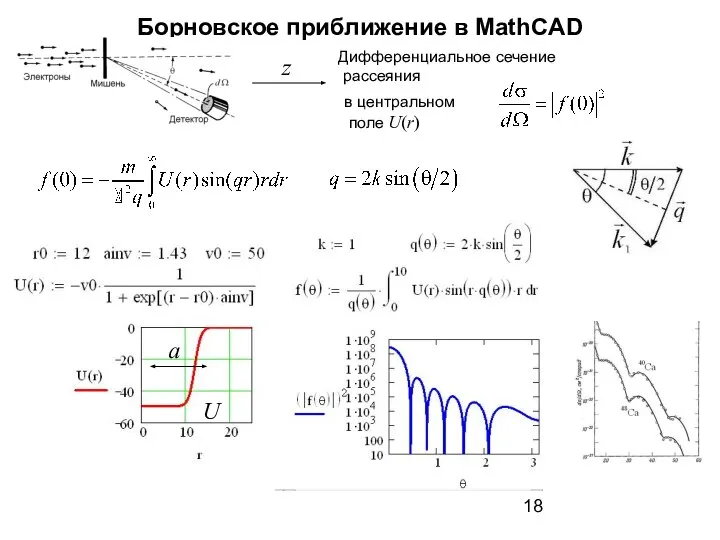
- 18. Борновское приближение в MathCAD Дифференциальное сечение рассеяния z a U в центральном поле U(r)
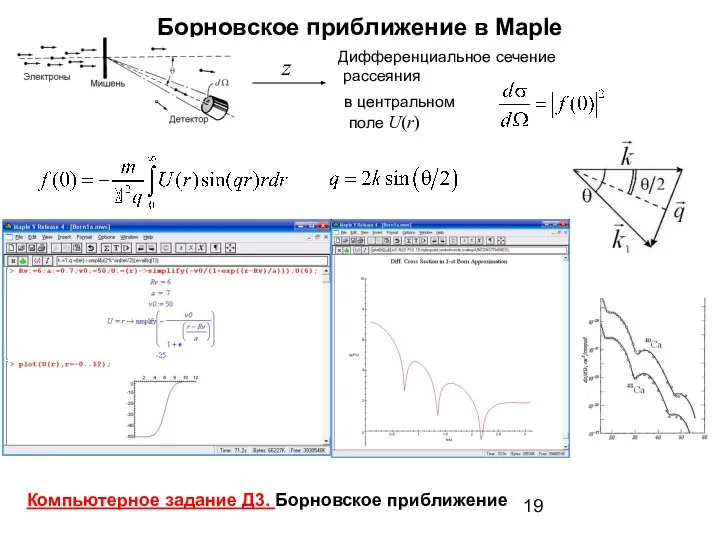
- 19. Борновское приближение в Maple Дифференциальное сечение рассеяния z в центральном поле U(r) Компьютерное задание Д3. Борновское
- 20. Борновское приближение в Maple Дифференциальное сечение рассеяния z в центральном поле U(r) Компьютерное задание Д3. Борновское
- 21. Парциальное разложение амплитуды рассеяния: волновая функция частицы в центральном поле Стационарное уравнение Шредингера
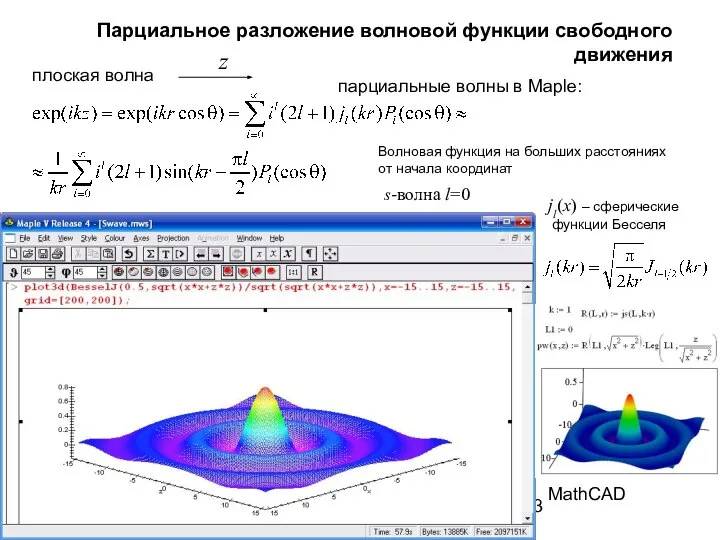
- 22. Парциальное разложение волновой функции свободного движения z плоская волна Волновая функция на больших расстояниях от начала
- 23. Парциальное разложение волновой функции свободного движения z плоская волна Волновая функция на больших расстояниях от начала
- 24. Парциальное разложение волновой функции свободного движения z плоская волна Волновая функция на больших расстояниях от начала
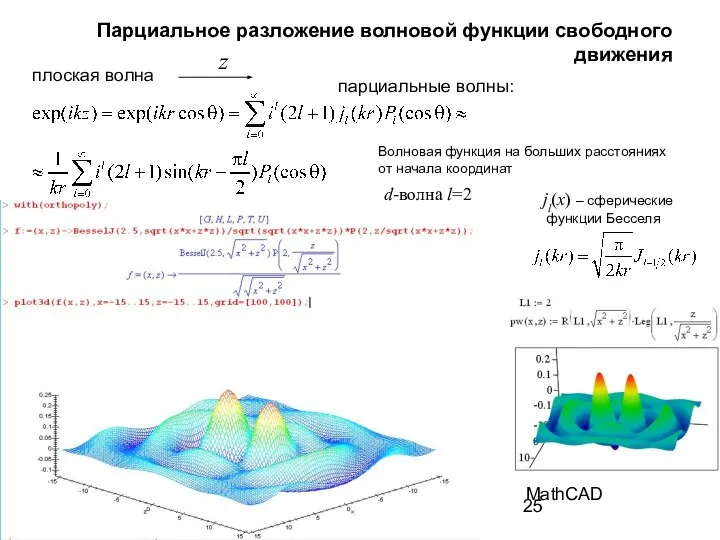
- 25. Парциальное разложение волновой функции свободного движения z плоская волна Волновая функция на больших расстояниях от начала
- 26. Парциальное разложение волновой функции и амплитуды рассеяния z Амплитуда рассеяния Плоская волна Волновая функция на больших
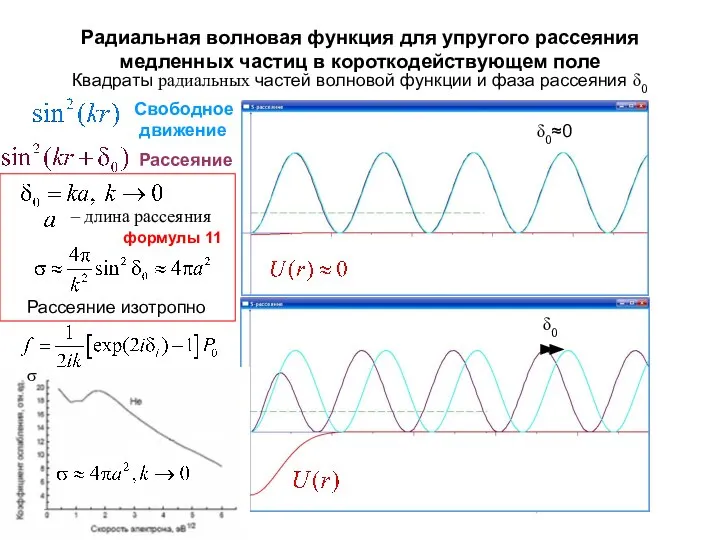
- 27. Радиальная волновая функция для упругого рассеяния медленных частиц в короткодействующем поле Квадраты радиальных частей волновой функции
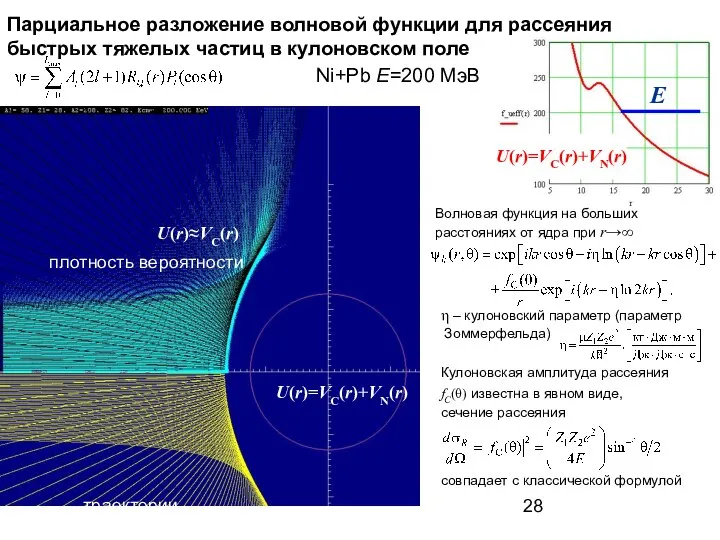
- 28. траектории плотность вероятности Ni+Pb E=200 МэВ Парциальное разложение волновой функции для рассеяния быстрых тяжелых частиц в
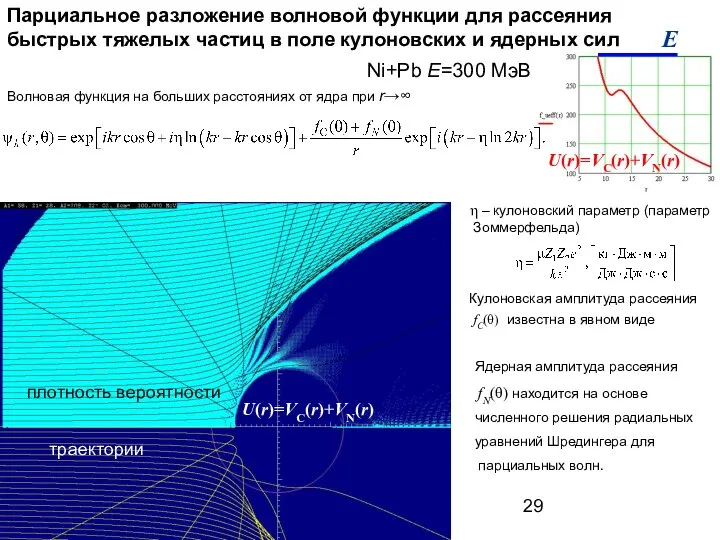
- 29. Парциальное разложение волновой функции для рассеяния быстрых тяжелых частиц в поле кулоновских и ядерных сил траектории
- 30. Оптическая модель упругого рассеяния Различные состояния, образующиеся после столкновения частиц, называют каналами реакции. Например, при столкновении
- 31. Компьютерное задание Д4 Оптическая модель упругого рассеяния Выполнить анализ экспериментальных данных по упругому рассеянию, (для максимальной
- 32. Компьютерное задание Д4 Оптическая модель упругого рассеяния Сетевая база знаний NRV по ядерной физике низких энергий.
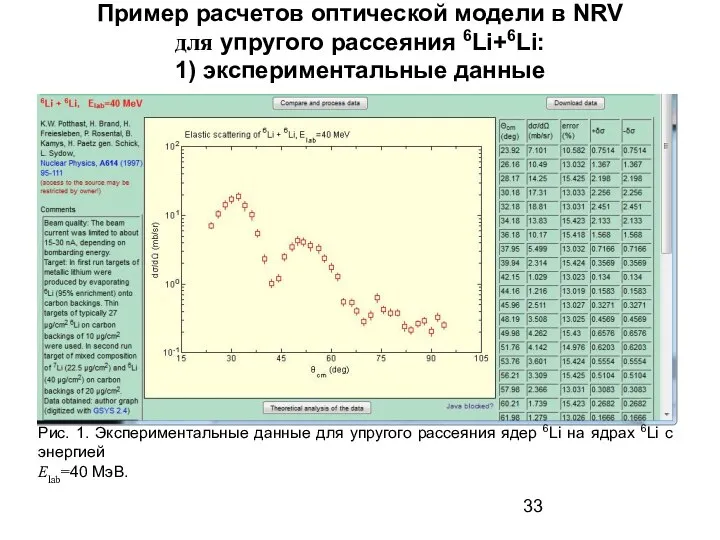
- 33. Пример расчетов оптической модели в NRV для упругого рассеяния 6Li+6Li: 1) экспериментальные данные Рис. 1. Экспериментальные
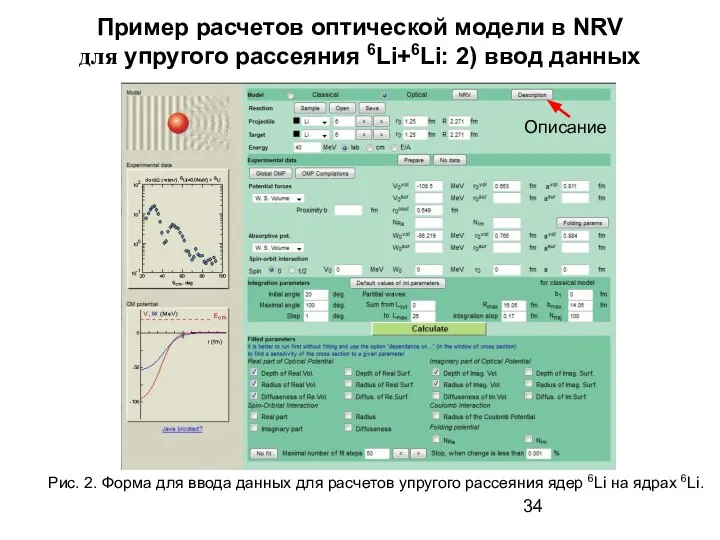
- 34. Пример расчетов оптической модели в NRV для упругого рассеяния 6Li+6Li: 2) ввод данных Рис. 2. Форма
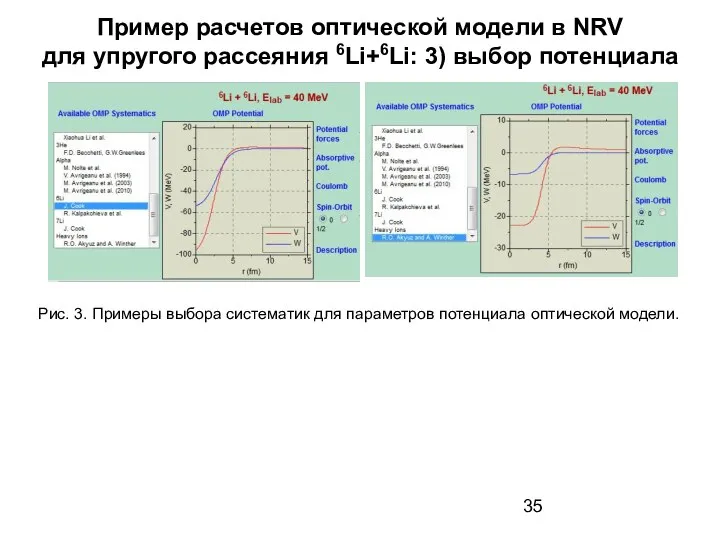
- 35. Пример расчетов оптической модели в NRV для упругого рассеяния 6Li+6Li: 3) выбор потенциала Рис. 3. Примеры
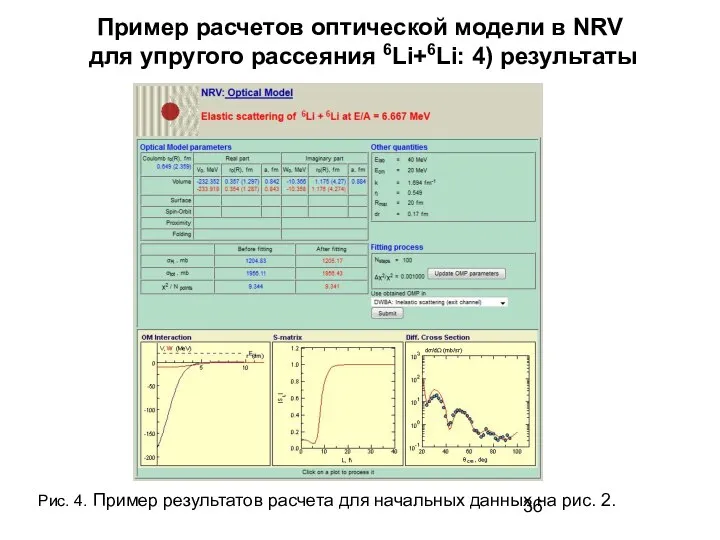
- 36. Пример расчетов оптической модели в NRV для упругого рассеяния 6Li+6Li: 4) результаты Рис. 4. Пример результатов
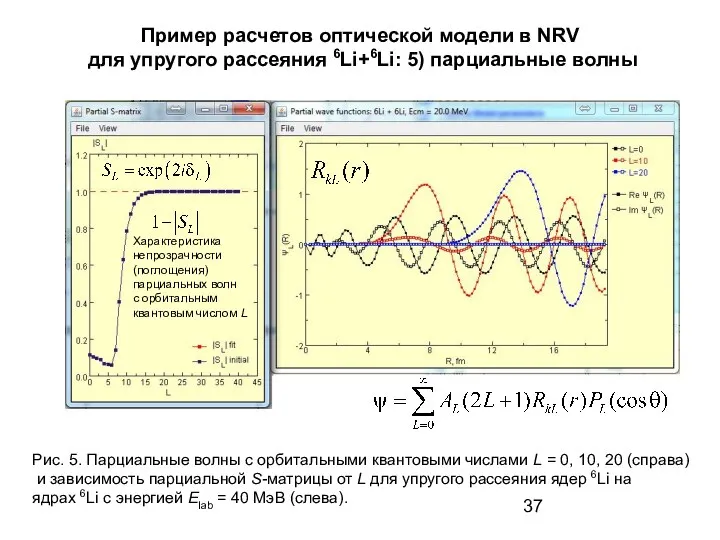
- 37. Пример расчетов оптической модели в NRV для упругого рассеяния 6Li+6Li: 5) парциальные волны Рис. 5. Парциальные
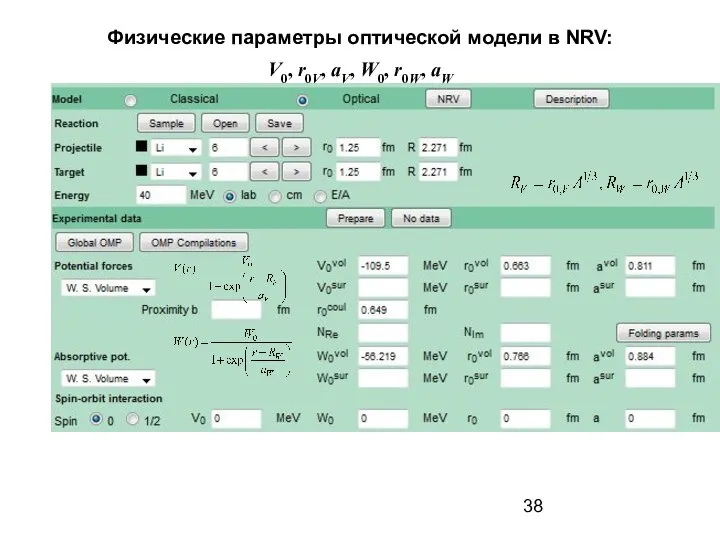
- 38. Физические параметры оптической модели в NRV: V0, r0V, aV, W0, r0W, aW
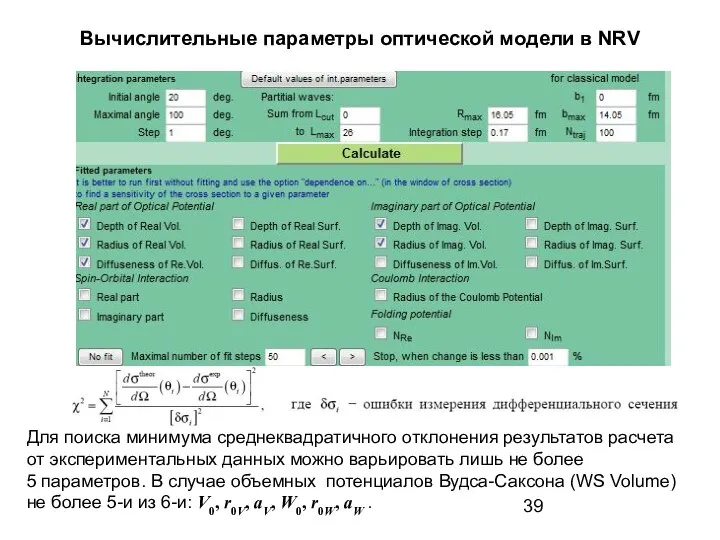
- 39. Вычислительные параметры оптической модели в NRV Для поиска минимума среднеквадратичного отклонения результатов расчета от экспериментальных данных
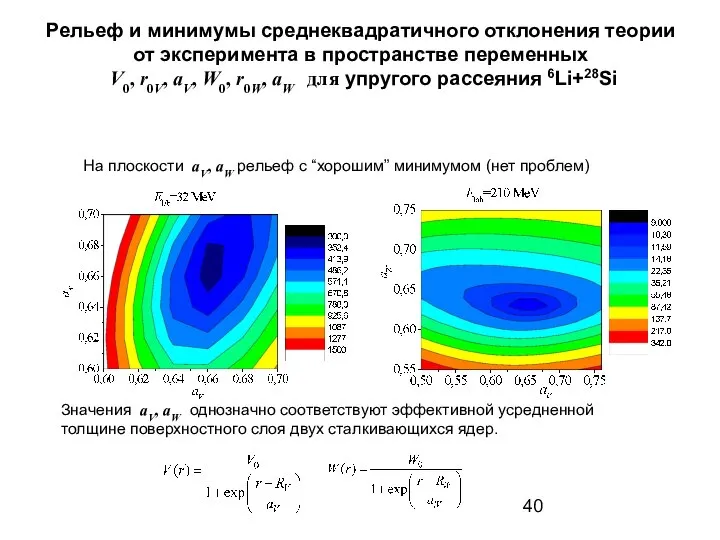
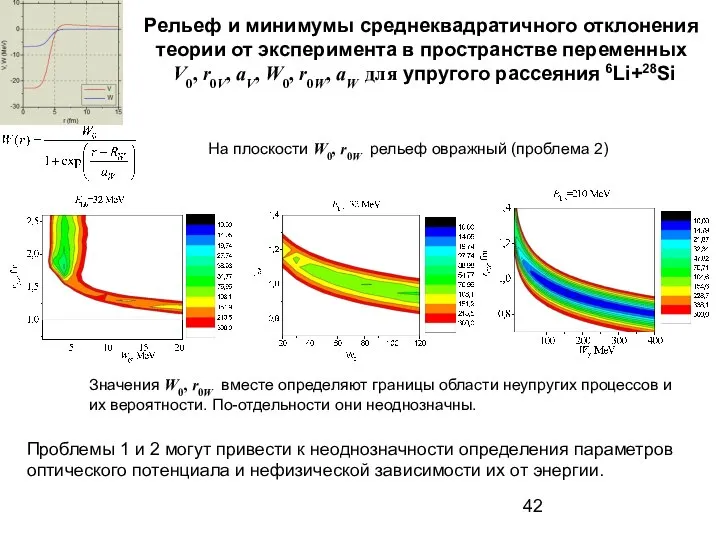
- 40. Рельеф и минимумы среднеквадратичного отклонения теории от эксперимента в пространстве переменных V0, r0V, aV, W0, r0W,
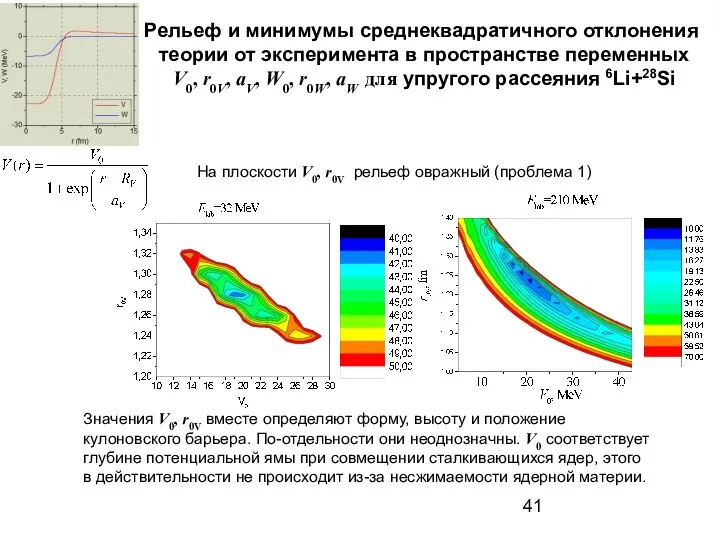
- 41. Рельеф и минимумы среднеквадратичного отклонения теории от эксперимента в пространстве переменных V0, r0V, aV, W0, r0W,
- 42. Рельеф и минимумы среднеквадратичного отклонения теории от эксперимента в пространстве переменных V0, r0V, aV, W0, r0W,
- 43. Литература Ландау Л.Д. Лифшиц Е.М. Краткий курс теоретической физики. Т. 2. Квантовая механика. − М. Наука.
- 44. Вопрос 9. Стационарная теория возмущений в отсутствие вырождения. Стационарная теория возмущений при наличии вырождения. Эффект Зеемана.
- 45. Стационарная теория возмущений в отсутствие вырождения Формулы 12 Поправки к энергии первого порядка в невырожденном случае
- 46. Стационарная теория возмущений при наличии вырождения секулярное уравнение Формулы 12 Поправки к энергии первого порядка в
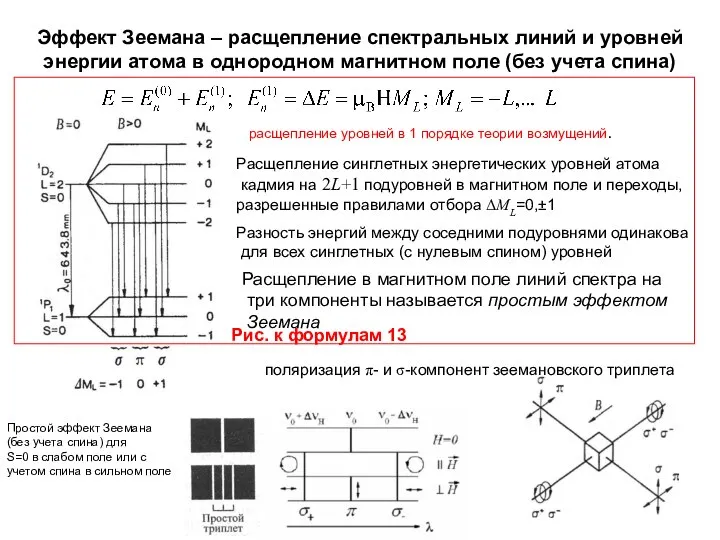
- 47. Эффект Зеемана – расщепление спектральных линий и уровней энергии атома в однородном магнитном поле (без учета
- 48. Эффект Зеемана – расщепление спектральных линий и уровней энергии атома в однородном магнитном поле (без учета
- 49. Эффект Зеемана – расщепление красной спектральной линии атома кадмия в однородном магнитном поле (без учета спина)
- 50. Эффект Штарка - расщепление спектральных линий и уровней энергии в однородном электрическом поле 1. Атом водорода:
- 51. Литература Сивухин, Д. В. Общий курс физики. В 5 Т. Т 5: Атомная и ядерная физика:
- 52. Вопрос 10 Уравнение Дирака. Квазирелятивистское приближение. Спин-орбитальное взаимодействие. Тонкая структура спектра атома водорода и атомов щелочных
- 53. Уравнение Дирака для свободного движения Матрицы Паули Состояния с определенным значением импульса p и энергии ε
- 54. Решения уравнения Дирака для атома водорода: уровни энергии СИ Гауссова система единиц точное выражение приближенное выражение
- 55. Решение уравнения Дирака для атома водорода: энергии точное выражение приближенные выражения приближенное выражение Энергия уровней атома
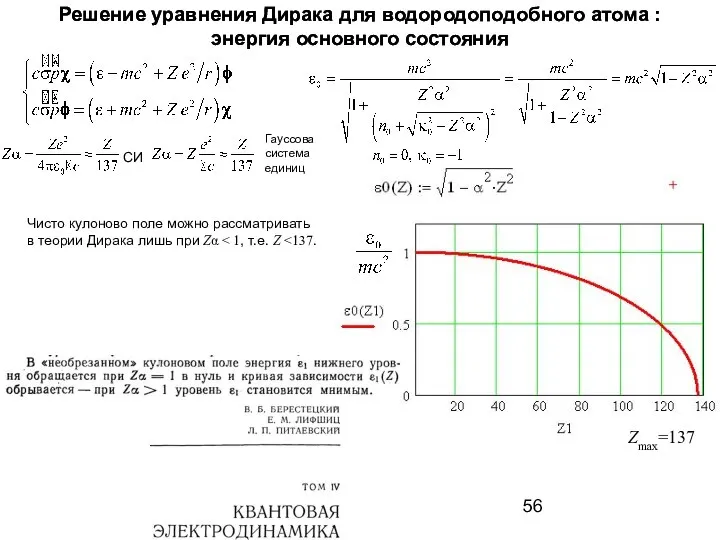
- 56. Решение уравнения Дирака для водородоподобного атома : энергия основного состояния СИ Гауссова система единиц Zmax=137 Решение
- 57. Решение уравнения Дирака для водородоподобного атома с ядром конечного размера: энергия основного состояния
- 58. Квазирелятивистское приближение. Нерелятивистское движение в слабом электромагнитном поле магнетон Бора Движение в слабом центральном электростатическом поле
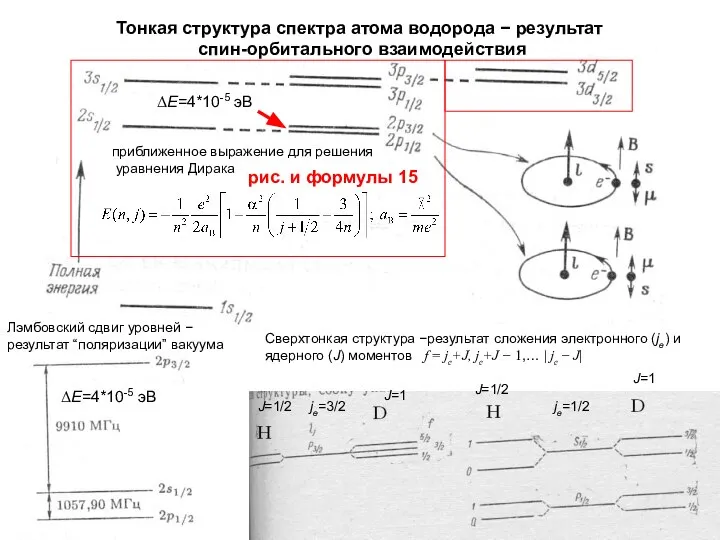
- 59. Спин-орбитальное взаимодействие. Схема образования дублетных линий главной и резкой серий натрия главная серия резкая серия Водород
- 60. Спин-орбитальное взаимодействие. Схема образования дублетных линий главной и резкой серий натрия главная серия резкая серия
- 61. Лэмбовский сдвиг уровней − результат “поляризации” вакуума Сверхтонкая структура −результат сложения электронного (je) и ядерного (J)
- 62. Литература Сивухин, Д. В. Общий курс физики. В 5 Т. Т 5: Атомная и ядерная физика:
- 63. Вопрос 11. Системы тождественных частиц. Бозоны и фермионы. Принцип Паули. Атом гелия.
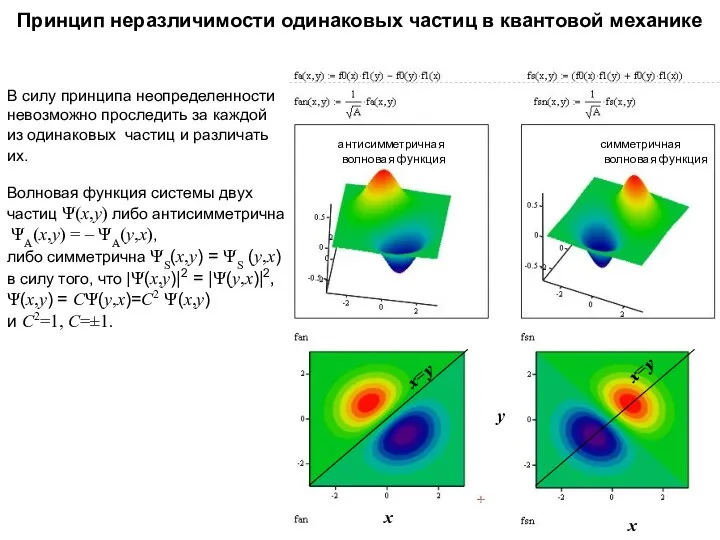
- 64. Принцип неразличимости одинаковых частиц в квантовой механике В силу принципа неопределенности невозможно проследить за каждой из
- 65. Системы тождественных частиц Ландау Л.Д. Лифшиц Е.М. Краткий курс теоретической физики. Т. 2. Квантовая механика. −
- 66. Бозоны и фермионы: связь спина со статистикой О частицах, описывающихся антисимметричными волновыми функциями, говорят как о
- 67. Вторичное квантование: спин и статистика В релятивистской квантовой теории полная энергия сохраняется, масса и полное число
- 68. Бозоны и фермионы: спин и статистика См. файл спин и статистика.pdf Формулы 17 Формулы 17
- 69. Бозоны и фермионы См. файл частицы.pdf
- 70. Принцип Паули
- 71. Система двух электронов Полная антисимметричная (по отношению к перестановке электронов) волновая функция системы двух электронов может
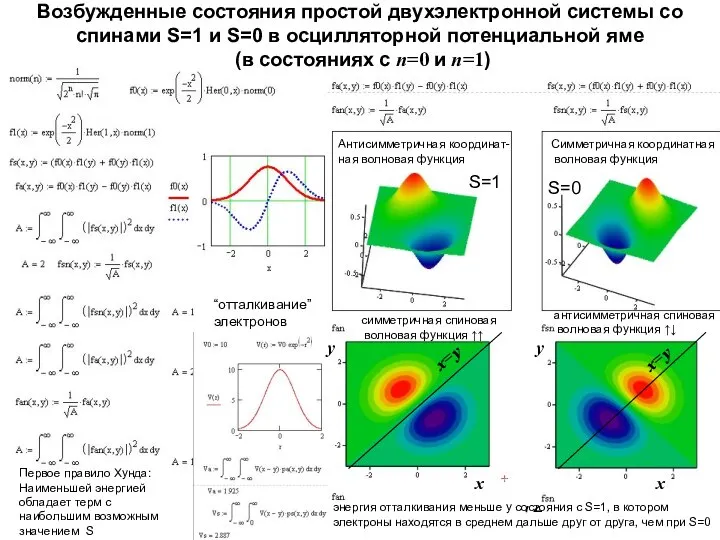
- 72. Возбужденные состояния простой двухэлектронной системы со спинами S=1 и S=0 в осцилляторной потенциальной яме (в состояниях
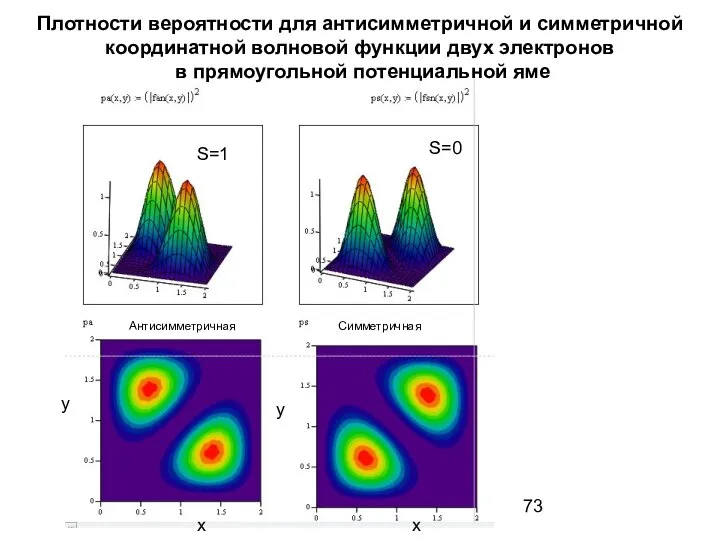
- 73. Плотности вероятности для антисимметричной и симметричной координатной волновой функции двух электронов в прямоугольной потенциальной яме x
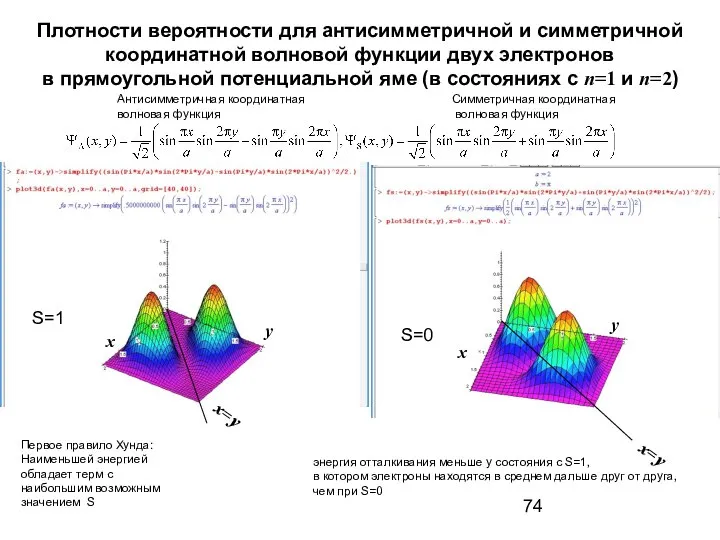
- 74. Плотности вероятности для антисимметричной и симметричной координатной волновой функции двух электронов в прямоугольной потенциальной яме (в
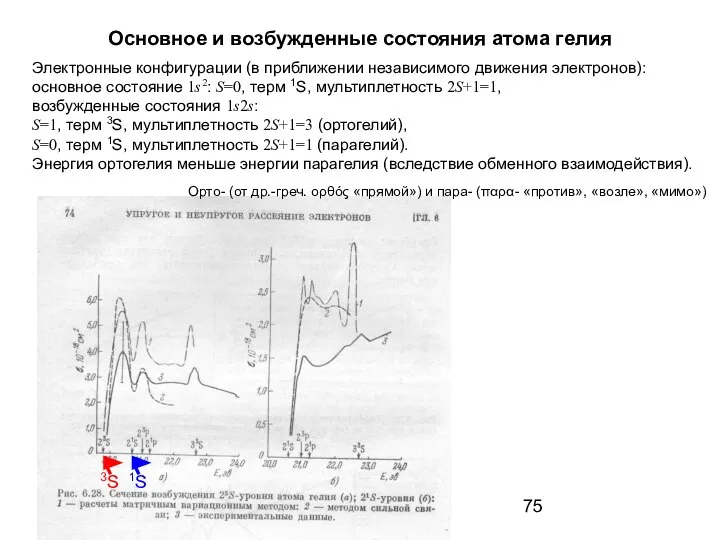
- 75. Основное и возбужденные состояния атома гелия Электронные конфигурации (в приближении независимого движения электронов): основное состояние 1s2:
- 77. Скачать презентацию













































 Закон Ома для полной цепи. Законы Кирхгофа
Закон Ома для полной цепи. Законы Кирхгофа Тепломассообмен. Теплопроводность
Тепломассообмен. Теплопроводность Обеспечение стойкости ЭС к электромагнитным и ионизирующим излучениям
Обеспечение стойкости ЭС к электромагнитным и ионизирующим излучениям Проводники и электростатическое поле
Проводники и электростатическое поле Течение и свойства жидкости
Течение и свойства жидкости Плотность разных тел и их свойства
Плотность разных тел и их свойства 1. Электростатика
1. Электростатика Эволюция механики
Эволюция механики Магнитное поле. Постоянные магниты и магнитное поле тока. Индукция магнитного поля
Магнитное поле. Постоянные магниты и магнитное поле тока. Индукция магнитного поля Механическая работа 8 класс - Презентация по физике_
Механическая работа 8 класс - Презентация по физике_ Колебания и волны
Колебания и волны Свободное падение
Свободное падение Професія зварювальник
Професія зварювальник Некоторые вопросы физики магнитных явлений
Некоторые вопросы физики магнитных явлений Характеристики интерференции двух пересекающихся широкополосных диспергированных пучков
Характеристики интерференции двух пересекающихся широкополосных диспергированных пучков Энергия. Работа. Закон сохранения механической энергии
Энергия. Работа. Закон сохранения механической энергии Газовые законы
Газовые законы Физика в нашей жизни
Физика в нашей жизни Электропитание и электроснабжение нетяговых потребителей
Электропитание и электроснабжение нетяговых потребителей Работу выполнила: Макарова Екатерина, ученица 7 класса, ГОУ СОШ № 546 г.Москвы Руководитель: Казакова Ю.В., учитель физики
Работу выполнила: Макарова Екатерина, ученица 7 класса, ГОУ СОШ № 546 г.Москвы Руководитель: Казакова Ю.В., учитель физики Нанотехнологии и науки о материалах
Нанотехнологии и науки о материалах Движение тела по окружности с постоянной по модулю скоростью.
Движение тела по окружности с постоянной по модулю скоростью. Мир в магнитах. При поддержке туристической компании «Колесница»
Мир в магнитах. При поддержке туристической компании «Колесница» Лазерная указка: мифы и реальность
Лазерная указка: мифы и реальность Презентация по физике "Рудольф Дизель. Немецкий изобретатель" - скачать
Презентация по физике "Рудольф Дизель. Немецкий изобретатель" - скачать  Механика. Механическое движение. Урок 1 9 класс
Механика. Механическое движение. Урок 1 9 класс Взаимодействие магнитного поля и проводников с током
Взаимодействие магнитного поля и проводников с током Двигатели внутреннего сгорания. Эксплуатация и ремонт базовых машин бронетанковой техники
Двигатели внутреннего сгорания. Эксплуатация и ремонт базовых машин бронетанковой техники