Измерение информации. Информационная характеристика источника двоичных сообщений

Введение

Измерение – нахождение значения физической величины опытным путем с помощью специальных

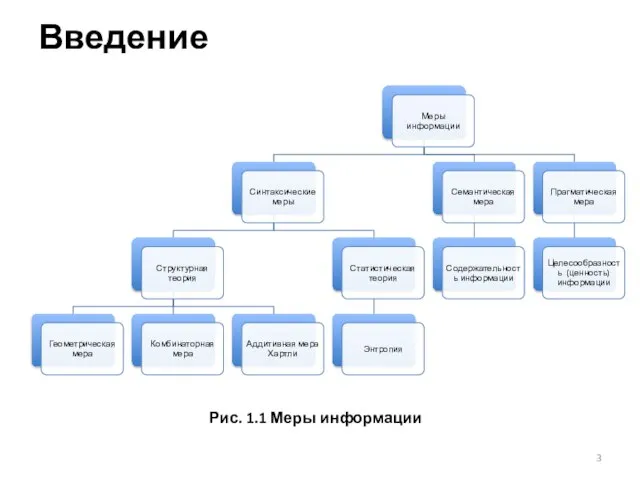
Введение

Рис. 1.1 Меры информации

Введение

В синтаксическом подходе выделяют:
Структурная теория рассматривает дискретное строение массивов информации и

1.1. Синтаксические меры информации. Структурная теория.

При использовании структурной теории (структурных мер)

1.1.1. Геометрическая мера

Определение количества информации геометрическим методом сводится к измерению длины

Пусть информация отражается полным комплексом XTN.
Если отсчеты по осям X, T,

К этой мере целесообразно прибегать тогда, когда требуется оценить возможность передачи

В комбинаторике рассматривают различные виды соединения из n элементов по m

Количество информации в комбинаторной мере вычисляется как количество комбинаций информационных элементов.
Т.е.

Например, при сочетаниях из n=10 по m=0, 1, 2, 3 …9,

Не всегда все возможные комбинации составляют действительные степени свободы данной системы.
Тогда

Из теории вероятностей:
Проводится некий опыт, исход которого называется событием.
Например, при бросании

Из теории вероятностей:
Меру случайности называют вероятностью и обозначают P(A).
Если P(A)=1, то

Из теории вероятностей:
Событие A называется независимым от события B, если P(A)

Из теории вероятностей:
События A и B называют несовместными, если в результате

Из теории вероятностей:
Суммой событий A и B называется событие, состоящее в

Из теории вероятностей:
Совокупность событий составляют полную группу, если в результате опыта

Рассмотрим 2 независимых опыта с числом равновероятных исходов N1 и N2
Предположим,

В зависимости от выбора основания логарифма получаем следующие меры количества информации:

Иной подход к выводу формулы Хартли:
Пусть передаваемое сообщение имеет вид числа,

В случае, когда все N состояний равновероятны, получаем следующую формулу для

При статистическом (вероятностном) подходе информация рассматривается как сообщения о случайных событиях

Последовательность знаков с таким свойством называется шенноновским сообщением.
Поскольку сами знаки и

Упорядоченным называется состояние системы, осуществляемое относительно малым числом способов, а беспорядочным

Рассмотрим в качестве системы сосуд, разделенный проницаемой перегородкой на две равные

1.2.1. Понятие энтропии

Таблица 1.1 Распределение четырех молекул в двух зонах

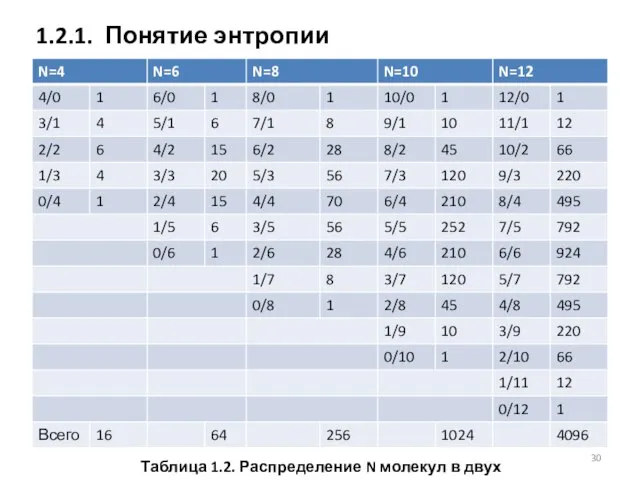
Формула:
K=N!/(N1!•N2!)=N!/[N1!•(N-N1)!]
С увеличением числа молекул различия в вероятностях будут резко возрастать (таблица

1.2.1. Понятие энтропии

Таблица 1.2. Распределение N молекул в двух зонах

Вероятность скопления N молекул газа в одной половине сосуда объемом 1

Второй закон термодинамики:
Природа стремится от состояний менее вероятных к состояниям более

Пример:
Если взять 4-разрядные двоичные числа, то в 6 комбинациях из 16

Энтропия в термодинамике – количественная мера неупорядоченности, мера вероятности осуществления какого-либо

Статистический смысл второго закона (начала) термодинамики:
Макроскопическое состояние газа с некоторыми значениями

В соответствии со вторым законом для замкнутого пространства (изолированной системы) энтропия

Иная трактовка - энтропия как мера вероятности осуществления какого-либо состояния системы:
S=-Σpi

Третий смысл энтропии получается из понятия упорядоченности: коль скоро неупорядоченные состояния

Энтропия в теории информации – количественная мера неопределенности.
Трактовку ввел в 1948

Главным свойством рассмотренных опытов является неопределенность, т.к. каждый исход – случайное

Для опыта с N равновероятными исходами x1, x2,…xN (полная группа случайных

Рассматривая количество информации как меру неопределенности такого опыта в соответствии с

В общем случае для опыта с N неравновероятными исходами:
Мера неопределенности:
H(X)=-p1 ld

H(X) – энтропия случайного опыта или просто энтропия.
H(X)=-Σpi ld pi при

Единице измерения энтропии 1 бит соответствует опыт, имеющий N=2 равновероятных исходов

Сопоставление термодинамической формулы (Больцмана) и информационной (Хартли и Шеннона) трактовок понятия

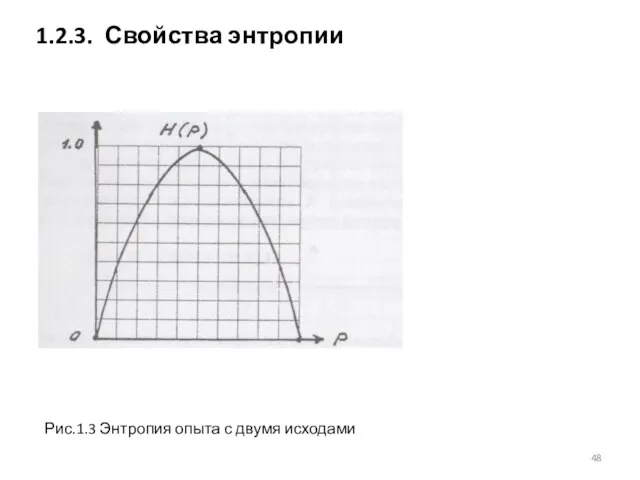
H(X) – величина вещественная и неотрицательная
H(X)min=0 когда pk=1, pi=1
H(X)max=ld N когда

1.2.3. Свойства энтропии

Рис.1.3 Энтропия опыта с двумя исходами

Условная энтропия HY(X) является мерой остаточной неопределенности.

1.2.4. Количество информации

Рис.1.4. Упрощенная схема

Пусть источник сообщений (испытатель), наблюдая за случайными исходами, генерирует и передает

Количество информации – числовая характеристика сигнала, позволяющая оценить исходную степень неопределенности,

Для латинского алфавита (26 букв) H=ld 26≈4,7 бит/букву
Для кириллицы (33 буквы)

Рассмотрим оценки, отвечающие как семантическому, так и прагматическому подходам.
Это обусловлено тем,

Оценка содержательности основана на математической логике, в которой логические функции истинности

Логическая оценка информации:
Отличие статистической оценки от логической состоит в том, что

А.А.Харткевичем предложена мера целесообразности информации, которая определяется как изменение вероятности достижения

Мера целесообразности в общем виде может выть выражена соотношением
I=Ld p1-ld p0=ld(p1/p0)
где

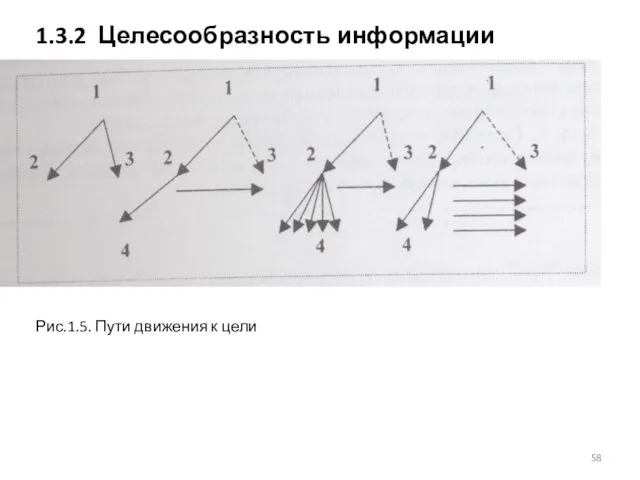
1.3.2 Целесообразность информации

Рис.1.5. Пути движения к цели

Пусть имеется некоторое исходное состояние (точка 1), цель (точка 3), и