Содержание
- 2. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ КУРСА
- 3. Что нужно знать: перевод чисел между десятичной, двоичной, восьмеричной и шестнадцатеричной системами счисления; желательно выучить наизусть
- 4. Теория Системы счисления бывают позиционные и непозиционные. Система счисления считают позиционной, если значение цифры в записи
- 5. Теория Для перевода целых чисел из десятичной системы в систему счисления с основанием q применяют метод
- 7. Р-06. Сколько единиц в двоичной записи восьмеричного числа 17318? Решение: для решения достаточно знать двоичные коды
- 8. Р-03. Даны 4 числа, они записаны с использованием различных систем счисления. Укажите среди этих чисел то,
- 9. Тема: ПОСТРОЕНИЕ И АНАЛИЗ ТАБЛИЦ ИСТИННОСТИ ЛОГИЧЕСКИХ ВЫРАЖЕНИЙ. Что нужно знать: условные обозначения логических операций ¬
- 10. Тема: ПОСТРОЕНИЕ И АНАЛИЗ ТАБЛИЦ ИСТИННОСТИ ЛОГИЧЕСКИХ ВЫРАЖЕНИЙ. Что нужно знать: условные обозначения логических операций ¬
- 11. Тема: ПОСТРОЕНИЕ И АНАЛИЗ ТАБЛИЦ ИСТИННОСТИ ЛОГИЧЕСКИХ ВЫРАЖЕНИЙ. §2. ОСНОВНЫЕ ПОНЯТИЯ МАТЕМАТИЧЕСКОЙ ЛОГИКИ Теория Аппарат математической
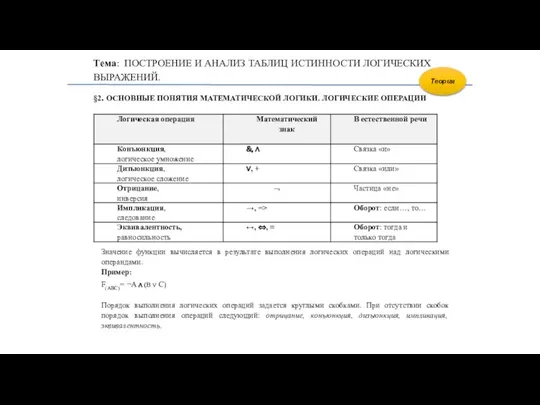
- 12. Тема: ПОСТРОЕНИЕ И АНАЛИЗ ТАБЛИЦ ИСТИННОСТИ ЛОГИЧЕСКИХ ВЫРАЖЕНИЙ. §2. ОСНОВНЫЕ ПОНЯТИЯ МАТЕМАТИЧЕСКОЙ ЛОГИКИ. ЛОГИЧЕСКИЕ ОПЕРАЦИИ Теория
- 13. Тема: ПОСТРОЕНИЕ И АНАЛИЗ ТАБЛИЦ ИСТИННОСТИ ЛОГИЧЕСКИХ ВЫРАЖЕНИЙ. §2. ОСНОВНЫЕ ПОНЯТИЯ МАТЕМАТИЧЕСКОЙ ЛОГИКИ. ТАБЛИЦЫ ИСТИННОСТИ Теория
- 14. Тема: ПОСТРОЕНИЕ И АНАЛИЗ ТАБЛИЦ ИСТИННОСТИ ЛОГИЧЕСКИХ ВЫРАЖЕНИЙ. §2. ОСНОВНЫЕ ПОНЯТИЯ МАТЕМАТИЧЕСКОЙ ЛОГИКИ. ЗАКОНЫ АЛГЕБРЫ ЛОГИКИ
- 15. Тема: ПОСТРОЕНИЕ И АНАЛИЗ ТАБЛИЦ ИСТИННОСТИ ЛОГИЧЕСКИХ ВЫРАЖЕНИЙ. §2. ОСНОВНЫЕ ПОНЯТИЯ МАТЕМАТИЧЕСКОЙ ЛОГИКИ. ЗАКОНЫ АЛГЕБРЫ ЛОГИКИ
- 16. Тема: ПОСТРОЕНИЕ И АНАЛИЗ ТАБЛИЦ ИСТИННОСТИ ЛОГИЧЕСКИХ ВЫРАЖЕНИЙ. ПРИМЕР
- 17. Тема: ПОСТРОЕНИЕ И АНАЛИЗ ТАБЛИЦ ИСТИННОСТИ ЛОГИЧЕСКИХ ВЫРАЖЕНИЙ. ПРИМЕР
- 18. §3. ИЗМЕРЕНИЕ ИНФОРМАЦИИ 3.1. Вероятностный подход 3.2. Алфавитный подход Теория
- 19. 4. АЛГОРИТМИЗАЦИЯ И ПРОГРАММИРОВАНИЕ 4.1. Алгоритм 4.2 Блок-схемы 4.3. Школьный алгоритмический язык 1.4.4. Базовые алгоритмические структуры
- 20. 5. РАБОТА В ТАБЛИЧНЫХ ПРОЦЕССОРАХ Теория
- 21. 6. ГРАФЫ Теория
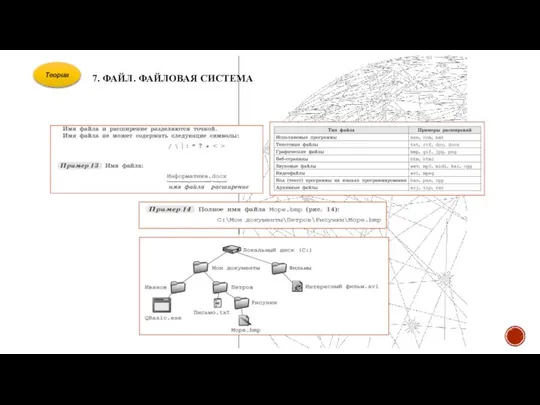
- 22. 7. ФАЙЛ. ФАЙЛОВАЯ СИСТЕМА Теория
- 23. 8. БАЗА ДАННЫХ Теория
- 24. 9. ИНФОРМАЦИОННО-КОММУНИКАЦИОННЫЕ ТЕХНОЛОГИИ 9.1. Интернет 9.2. Службы (сервисы) Интернета Поиск информации 9.3. Протоколы передачи данных Теория
- 25. РАЗБОР ТЕМАТИЧЕСКИХ ЗАДАНИЙ «Редакция «Поколение V»
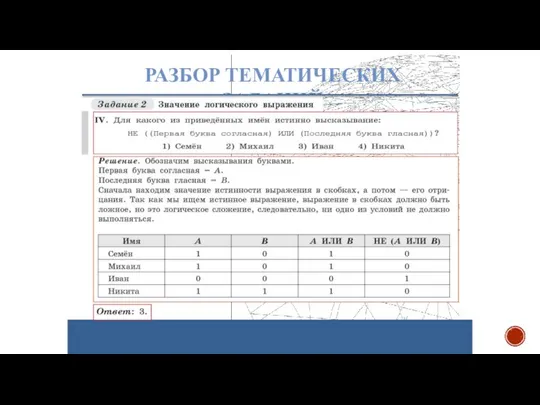
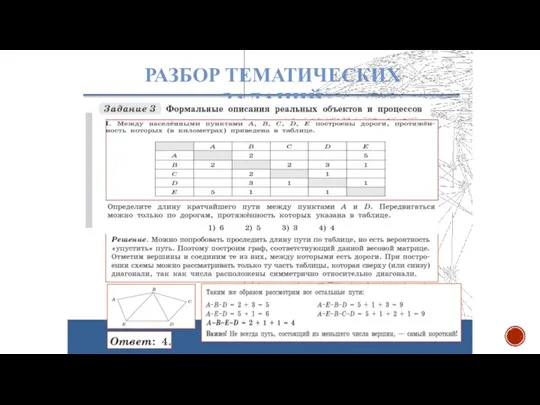
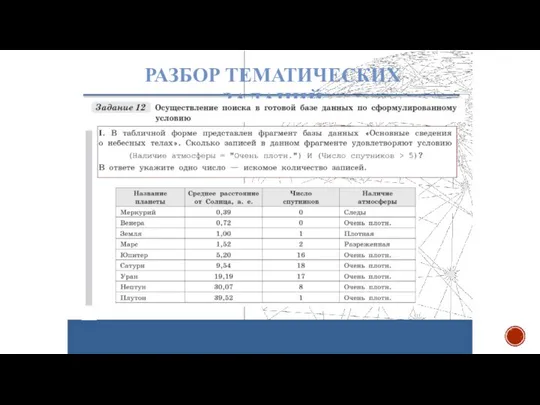
- 26. РАЗБОР ТЕМАТИЧЕСКИХ ЗАДАНИЙ
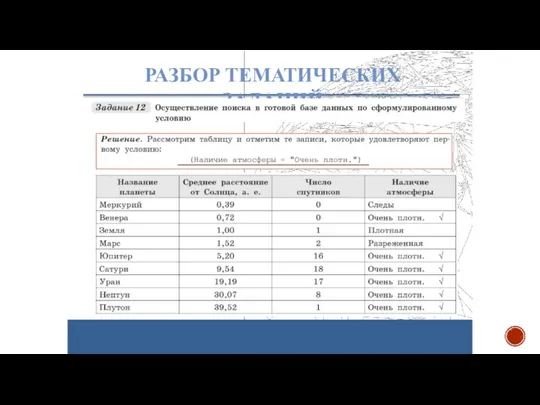
- 27. РАЗБОР ТЕМАТИЧЕСКИХ ЗАДАНИЙ
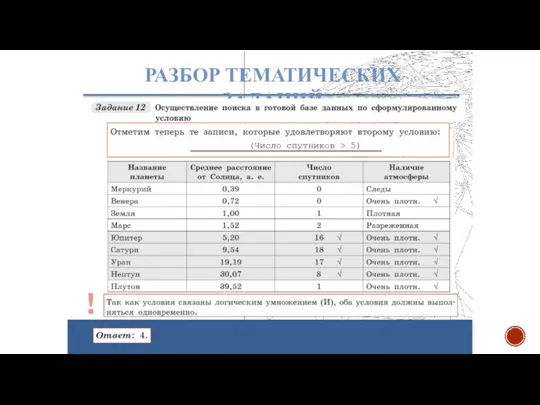
- 28. РАЗБОР ТЕМАТИЧЕСКИХ ЗАДАНИЙ
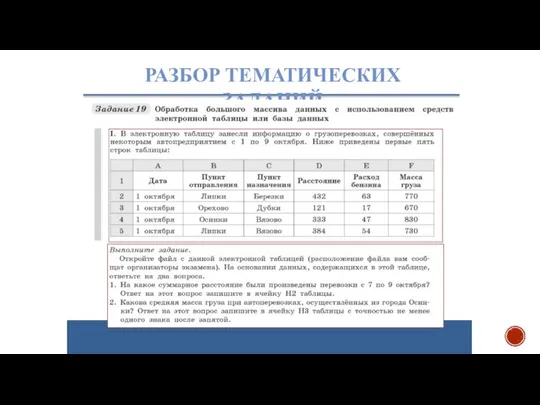
- 29. РАЗБОР ТЕМАТИЧЕСКИХ ЗАДАНИЙ
- 30. РАЗБОР ТЕМАТИЧЕСКИХ ЗАДАНИЙ
- 31. РАЗБОР ТЕМАТИЧЕСКИХ ЗАДАНИЙ
- 32. РАЗБОР ТЕМАТИЧЕСКИХ ЗАДАНИЙ
- 33. РАЗБОР ТЕМАТИЧЕСКИХ ЗАДАНИЙ
- 34. РАЗБОР ТЕМАТИЧЕСКИХ ЗАДАНИЙ
- 35. РАЗБОР ТЕМАТИЧЕСКИХ ЗАДАНИЙ
- 36. РАЗБОР ТЕМАТИЧЕСКИХ ЗАДАНИЙ
- 37. РАЗБОР ТЕМАТИЧЕСКИХ ЗАДАНИЙ
- 38. РАЗБОР ТЕМАТИЧЕСКИХ ЗАДАНИЙ
- 39. РАЗБОР ТЕМАТИЧЕСКИХ ЗАДАНИЙ
- 40. РАЗБОР ТЕМАТИЧЕСКИХ ЗАДАНИЙ
- 41. РАЗБОР ТЕМАТИЧЕСКИХ ЗАДАНИЙ
- 42. РАЗБОР ТЕМАТИЧЕСКИХ ЗАДАНИЙ !
- 43. РАЗБОР ТЕМАТИЧЕСКИХ ЗАДАНИЙ !
- 44. РАЗБОР ТЕМАТИЧЕСКИХ ЗАДАНИЙ
- 45. РАЗБОР ТЕМАТИЧЕСКИХ ЗАДАНИЙ
- 46. РАЗБОР ТЕМАТИЧЕСКИХ ЗАДАНИЙ !
- 47. РАЗБОР ТЕМАТИЧЕСКИХ ЗАДАНИЙ
- 48. РАЗБОР ТЕМАТИЧЕСКИХ ЗАДАНИЙ
- 49. РАЗБОР ТЕМАТИЧЕСКИХ ЗАДАНИЙ
- 50. РАЗБОР ТЕМАТИЧЕСКИХ ЗАДАНИЙ !
- 51. РАЗБОР ТЕМАТИЧЕСКИХ ЗАДАНИЙ
- 52. РАЗБОР ТЕМАТИЧЕСКИХ ЗАДАНИЙ ! Исходная цепочка начинается с символа, значит, добавляем 1 в начало и конец.
- 53. РАЗБОР ТЕМАТИЧЕСКИХ ЗАДАНИЙ ! Запомните: протокол — сервер — файл
- 54. РАЗБОР ТЕМАТИЧЕСКИХ ЗАДАНИЙ
- 55. РАЗБОР ТЕМАТИЧЕСКИХ ЗАДАНИЙ ! А Б В Г
- 56. РАЗБОР ТЕМАТИЧЕСКИХ ЗАДАНИЙ
- 57. РАЗБОР ТЕМАТИЧЕСКИХ ЗАДАНИЙ
- 58. РАЗБОР ТЕМАТИЧЕСКИХ ЗАДАНИЙ
- 59. РАЗБОР ТЕМАТИЧЕСКИХ ЗАДАНИЙ
- 60. РАЗБОР ТЕМАТИЧЕСКИХ ЗАДАНИЙ
- 61. РАЗБОР ТЕМАТИЧЕСКИХ ЗАДАНИЙ Алгоритм может быть выполнен в среде формального исполнителя или записан в текстовом редакторе.
- 63. Скачать презентацию




















































 Информационные технологии в журналистике Выполнила: Вера Букина, ИФиЯК
Информационные технологии в журналистике Выполнила: Вера Букина, ИФиЯК Операторы языка программирования Pascal
Операторы языка программирования Pascal Многообразие схем и сферы их применения
Многообразие схем и сферы их применения Системные вызовы семейства exec
Системные вызовы семейства exec Информация и информационные процессы
Информация и информационные процессы Перевод дробных и произвольных чисел из одной системы счисления в другую
Перевод дробных и произвольных чисел из одной системы счисления в другую Числа от 11 до 20. Нумерация. Проверочная работа №1.
Числа от 11 до 20. Нумерация. Проверочная работа №1. Кодирование звуковой информации
Кодирование звуковой информации Магистрально-модульный принцип построения компьютера
Магистрально-модульный принцип построения компьютера Linux Basics
Linux Basics Основы Web-дизайна Введение в сайтостроение
Основы Web-дизайна Введение в сайтостроение Создание сайта самостоятельно (02)
Создание сайта самостоятельно (02) Скоринг бюро 3.0
Скоринг бюро 3.0 Экономика информационных систем. Внешнее информационное обеспечение. Документы и их разработка
Экономика информационных систем. Внешнее информационное обеспечение. Документы и их разработка Сетевые технологии
Сетевые технологии Линейный алгоритм
Линейный алгоритм Exam
Exam Мы в современном медиапространстве: уважение, безопасность, достоверность
Мы в современном медиапространстве: уважение, безопасность, достоверность Word Pad мәтіндік редакторымен жұмыс
Word Pad мәтіндік редакторымен жұмыс «Использование мультимедийных возможностей при разработке приложений» Delphi. Тема 14:
«Использование мультимедийных возможностей при разработке приложений» Delphi. Тема 14: Разработка базы данных «Магазин канцелярских товаров» в УБД MS ACCESS
Разработка базы данных «Магазин канцелярских товаров» в УБД MS ACCESS Основы программирования на языке высокого уровня
Основы программирования на языке высокого уровня Презентация "РАБОТА С ОБЪЕКТАМИ ТЕКСТОВОГО ДОКУМЕНТА" - скачать презентации по Информатике
Презентация "РАБОТА С ОБЪЕКТАМИ ТЕКСТОВОГО ДОКУМЕНТА" - скачать презентации по Информатике Форма отчета по продажам
Форма отчета по продажам Кодирование информации в компьютере
Кодирование информации в компьютере MS WORD. Создание таблиц в текстовом редакторе
MS WORD. Создание таблиц в текстовом редакторе Диаграммы в Excel
Диаграммы в Excel Історія створення Windows
Історія створення Windows