Содержание
- 2. ДЕРЕВЬЯ РЕШЕНИЙ Деревья решений – это способ представления правил в иерархической, последовательной структуре, где каждому объекту
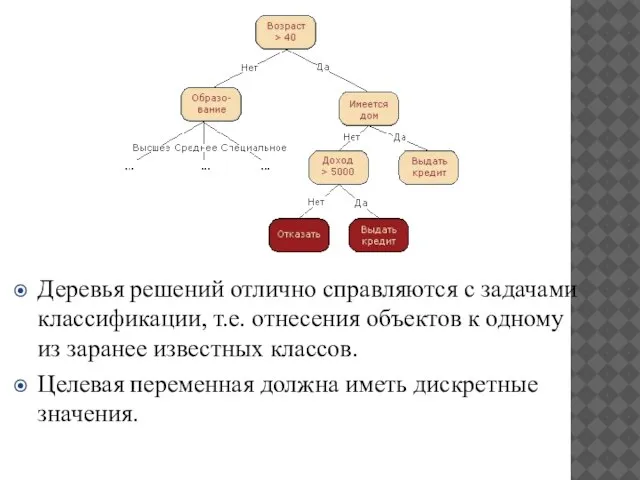
- 3. Деревья решений отлично справляются с задачами классификации, т.е. отнесения объектов к одному из заранее известных классов.
- 4. КАК ПОСТРОИТЬ ДЕРЕВО РЕШЕНИЙ? Задано некоторое обучающее множество T, содержащее объекты (примеры), каждый из которых характеризуется
- 5. ПУСТЬ ЧЕРЕЗ {C1, C2, ... CK} ОБОЗНАЧЕНЫ КЛАССЫ, ТОГДА СУЩЕСТВУЮТ 3 СИТУАЦИИ: множество T содержит один
- 6. Поскольку все объекты были заранее отнесены к известным нам классам, такой процесс построения дерева решений называется
- 7. ЭТАПЫ ПОСТРОЕНИЯ ДЕРЕВЬЕВ РЕШЕНИЙ При построении деревьев решений особое внимание уделяется следующим вопросам: выбору критерия признака,
- 8. ПРАВИЛО РАЗБИЕНИЯ. КАКИМ ОБРАЗОМ СЛЕДУЕТ ВЫБРАТЬ ПРИЗНАК? Для построения дерева на каждом внутреннем узле необходимо найти
- 9. Статистический критерий Алгоритм CART использует так называемый индекс Gini (в честь итальянского экономиста Corrado Gini), который
- 10. ФУНКЦИИ MATLAB ДЛЯ РАБОТЫ С ДЕРЕВОМ РЕШЕНИЙ. Расчет бинарного дерева классификации наблюдений T = treefit(X,y) функция
- 11. Графическое представление бинарного дерева классификации наблюдений treedisp(T) функция позволяет получить графическое представление бинарного дерева для классификации
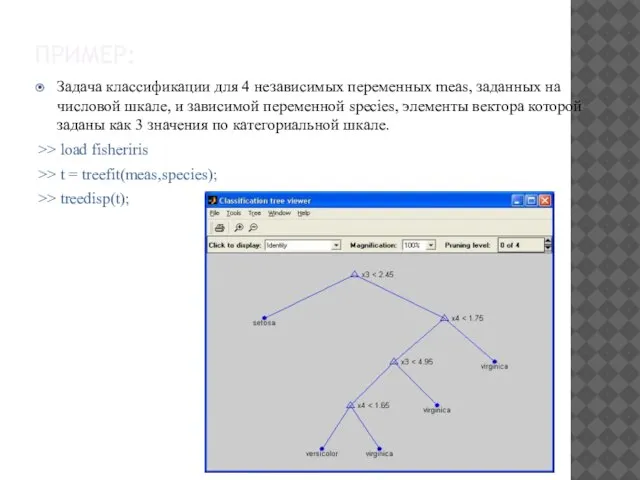
- 12. ПРИМЕР: Задача классификации для 4 независимых переменных meas, заданных на числовой шкале, и зависимой переменной species,
- 13. Расчет погрешности классификации на основе дерева решений cost = treetest(T,'resubstitution') функция позволяет рассчитать погрешность классификации, определяемой
- 14. [cost,secost,ntnodes,bestsize] = treetest(...) функция позволяет рассчитать: 1. cost - вектор погрешностей классификации; 2. secost - вектор
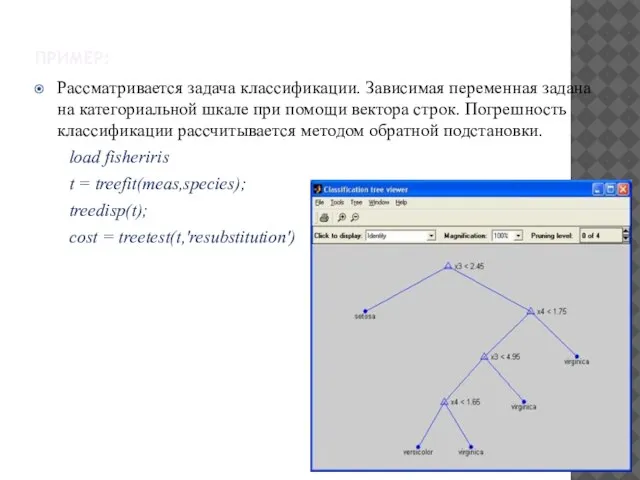
- 15. ПРИМЕР: Рассматривается задача классификации. Зависимая переменная задана на категориальной шкале при помощи вектора строк. Погрешность классификации
- 16. Расчет зависимой переменной по дереву классификации YFIT = treeval(T,X) функция позволяет определить значения зависимой переменной YFIT
- 17. [YFIT,NODE] = treeval(...) кроме значений зависимой переменной функция возвращает массив номеров узлов NODE соотнесенных c каждой
- 18. Пример совместного использования функций работы с деревом решений: load fisheriris; t1 = treefit(meas,species, 'names',{'SL' 'SW' 'PL'
- 19. Расчет параметров бинарного дерева решений T2 = treeprune(T1,'level',level) функция предназначена для получения сокращенной до уровня 'level'
- 20. ФУНКЦИИ FUZZY LOGIC TOOLBOX ДЛЯ РАБОТЫ С FIS plotfis ( fis ) Функция plotfis выводит в
- 21. fis = newfis(fis_name, fis_type) Создает в рабочей области новую систему нечеткого логического вывода. Функция newfis может
- 22. FIS_name= addvar (FIS_name, varType, varName, varBound) Добавляет переменную в систему нечеткого логического вывода. Переменную можно добавить
- 23. FIS_name=addmf(FIS_name, varType, varIndex, mfName, mfType, mfParams) Функцию принадлежности можно добавить только к существующей в рабочей области
- 24. Пример: FIS_name=addmf(FIS_name, ‘input’, 1, ‘низкий’, ‘trapmf’, [150, 155, 165, 170]) Строка добавляет в терм-множество первой входной
- 25. Матрица правил должна быть задана в формате indexed. Количество строк матрицы ruleList равно количеству добавляемых правил,
- 26. Пример: FIS_name=addrule(FIS_name, [1 1 1 1 1; 1 2 2 0.5 1]) Строка добавляет в базу
- 27. ПРИМЕР СОВМЕСТНОГО ИСПОЛЬЗОВАНИЯ ДЕРЕВА РЕШЕНИЙ И НЕЧЕТКОГО ВЫВОДА В качестве примера возьмем выборку ирисов Фишера, в
- 28. load fisheriris %Загрузка файла P_train1=meas(1:25,:);%Формирование обучающей P_train2=meas(51:75,:);% последовательности P_train3=meas(101:125,:); P_train=[P_train1;P_train2;P_train3]; T_train(1:25,1)='1';%Формирование группировочных данных T_train(26:50,1)='2';%для обучающей последовательности
- 29. P_ch1=meas(26:50,:); %Формирование контролирующей выборки P_ch2=meas(76:100,:); P_ch3=meas(126:150,:); P_ch=[P_ch1;P_ch2;P_ch3]; X_ch=treeval(tmin,P_ch); fis = newfis('spect.fis','sugeno'); %Создание системы нечеткого вывода fis
- 30. fis = addmf(fis,'output',1,'klass1','constant',1); fis = addmf(fis,'output',1,'klass2','constant',2); fis = addmf(fis,'output',1,'klass3','constant',3); ruleList=[ 1 0 1 1 1; 2
- 31. ПОДСЧЕТ КОЛИЧЕСТВА СОВПАДЕНИЙ TR_TRAIN1=size(find(X_train(1:25)==1),1) TR_TRAIN2=size(find(X_train(26:50)==2),1) TR_TRAIN3=size(find(X_train(51:75)==3),1) FS_TRAIN1=size(find(Y_train(1:25)==1),1) FS_TRAIN2=size(find(Y_train(26:50)==2),1) FS_TRAIN3=size(find(Y_train(51:75)==3),1) TR_CH1=size(find(X_ch(1:25)==1),1) TR_CH2=size(find(X_ch(26:50)==2),1) TR_CH3=size(find(X_ch(51:75)==3),1) FS_CH1=size(find(Y_ch(1:25)==1),1) FS_TRAIN2=size(find(Y_ch(26:50)==2),1) FS_TRAIN3=size(find(Y_ch(51:75)==3),1)
- 33. Скачать презентацию










![[cost,secost,ntnodes,bestsize] = treetest(...) функция позволяет рассчитать: 1. cost - вектор погрешностей](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/564924/slide-13.jpg)

![[YFIT,NODE] = treeval(...) кроме значений зависимой переменной функция возвращает массив номеров](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/564924/slide-16.jpg)






![Пример: FIS_name=addmf(FIS_name, ‘input’, 1, ‘низкий’, ‘trapmf’, [150, 155, 165, 170]) Строка](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/564924/slide-23.jpg)



![load fisheriris %Загрузка файла P_train1=meas(1:25,:);%Формирование обучающей P_train2=meas(51:75,:);% последовательности P_train3=meas(101:125,:); P_train=[P_train1;P_train2;P_train3]; T_train(1:25,1)='1';%Формирование](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/564924/slide-27.jpg)
![P_ch1=meas(26:50,:); %Формирование контролирующей выборки P_ch2=meas(76:100,:); P_ch3=meas(126:150,:); P_ch=[P_ch1;P_ch2;P_ch3]; X_ch=treeval(tmin,P_ch); fis = newfis('spect.fis','sugeno');](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/564924/slide-28.jpg)


 Алгоритмы и структуры данных. Лекция 7. Рекурсия
Алгоритмы и структуры данных. Лекция 7. Рекурсия Измерение информации
Измерение информации Особенности ведения предпринимательской деятельности в сети Интернет. Понятие электронной оферты и акцепта. Заключение договора
Особенности ведения предпринимательской деятельности в сети Интернет. Понятие электронной оферты и акцепта. Заключение договора ЦОР – цифровые образовательные ресурсы в обучении иностранному языку
ЦОР – цифровые образовательные ресурсы в обучении иностранному языку Современный компьютер
Современный компьютер Воробьева Людмила Васильевна Воробьева Людмила Васильевна МБОУ «СОШ № 9» город Вязники, Владимирской обл.
Воробьева Людмила Васильевна Воробьева Людмила Васильевна МБОУ «СОШ № 9» город Вязники, Владимирской обл. Субд access. Создание таблиц, запросов
Субд access. Создание таблиц, запросов Реализация проекта Память объединяет нас
Реализация проекта Память объединяет нас Позиционирование блоков исходя из структуры сайта
Позиционирование блоков исходя из структуры сайта Файловая система
Файловая система Интернет в жизни старшеклассника: за и против
Интернет в жизни старшеклассника: за и против Продажа авиабилетов на все направления
Продажа авиабилетов на все направления Сетевые информационные системы
Сетевые информационные системы Аналитическая программа SteamCardsFarmer
Аналитическая программа SteamCardsFarmer Информационная культура
Информационная культура Урок и голосовой помощник Маруся
Урок и голосовой помощник Маруся Linux Basics
Linux Basics Босова Людмила Леонидовна akulll@mail.ru
Босова Людмила Леонидовна akulll@mail.ru  Создание видео Безопасность детей в интернете
Создание видео Безопасность детей в интернете Презентация на тему Кодирование информации
Презентация на тему Кодирование информации Создание анимации, Знакомство с программой GIF ANImator.
Создание анимации, Знакомство с программой GIF ANImator. Устройство компьютера
Устройство компьютера Работа в Word
Работа в Word Открытый урок на тему: «Двоичная система счисления. Перевод из двоичной с.с в десятичную.» Учитель: Смаилова Ш.Т. КГУ «Средняя обще
Открытый урок на тему: «Двоичная система счисления. Перевод из двоичной с.с в десятичную.» Учитель: Смаилова Ш.Т. КГУ «Средняя обще Информатика ғылым және орта мектептегі оқу пәні ретінде
Информатика ғылым және орта мектептегі оқу пәні ретінде Компьютерная графика: области применения. Понятие растровой и векторной графики
Компьютерная графика: области применения. Понятие растровой и векторной графики Информационная безопасность. Общие принципы. (Лекция 1)
Информационная безопасность. Общие принципы. (Лекция 1) Приспособленец. Оптимизация работы с памятью путём предотвращения создания экземпляров элементов, имеющих общую сущность
Приспособленец. Оптимизация работы с памятью путём предотвращения создания экземпляров элементов, имеющих общую сущность