Содержание
- 2. Линейная алгебра. Основные сведения о матрицах. Виды и свойства матриц. Операции над матрицами.
- 3. 1. Понятие матрицы Определение. Прямоугольная таблица чисел, содержащая т строк и п столбцов, называется матрицей размера
- 4. или
- 5. Определение. Две матрицы А и В одного размера называются равными, если они совпадают поэлементно, т.е. А
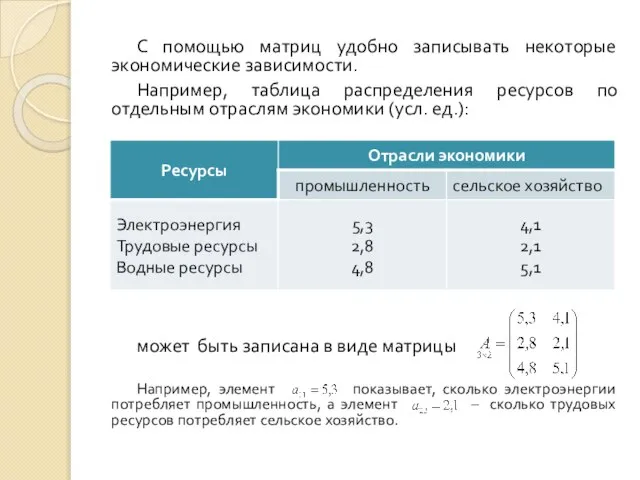
- 6. С помощью матриц удобно записывать некоторые экономические зависимости. Например, таблица распределения ресурсов по отдельным отраслям экономики
- 7. 2. Виды матриц Определение. Матрица, состоящая из одной строки, называется матрицей (вектором)-строкой, а из одного столбца
- 8. Определение. Если число столбцов матрицы п равно числу ее строк, то матрицу называют квадратной п-го порядка.
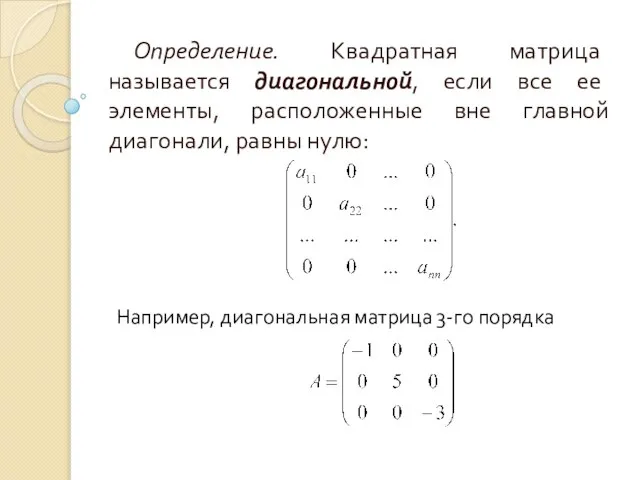
- 9. Определение. Квадратная матрица называется диагональной, если все ее элементы, расположенные вне главной диагонали, равны нулю: Например,
- 10. Если у диагональной матрицы п-го порядка все диагональные элементы равны единице, то матрица называется единичной п-го
- 11. Определение. Матрица любого размера называется нулевой или нуль – матрицей, если все ее элементы равны нулю:
- 12. Определение. Квадратная матрица называется треугольной, если все ее элементы, расположенные по одну сторону от главной диагонали,
- 13. 3. Операции над матрицами 1) Умножение матрицы на число. Определение. Произведением матрицы А на число λ
- 14. Например, Если , то . Следствие. Общий множитель всех элементов матрицы можно выносить за знак матрицы.
- 15. 2) Сложение матриц Определение. Суммой матриц А и В одинакового размера называется матрица С = А
- 16. Например, Частный случай: А + О = А.
- 17. 3) Вычитание матриц Определение. Разность двух матриц одинакового размера определяется через предыдущие операции: А – В
- 18. 4) Умножение матриц. Матрицу А можно умножить на матрицу В только в том случае, когда число
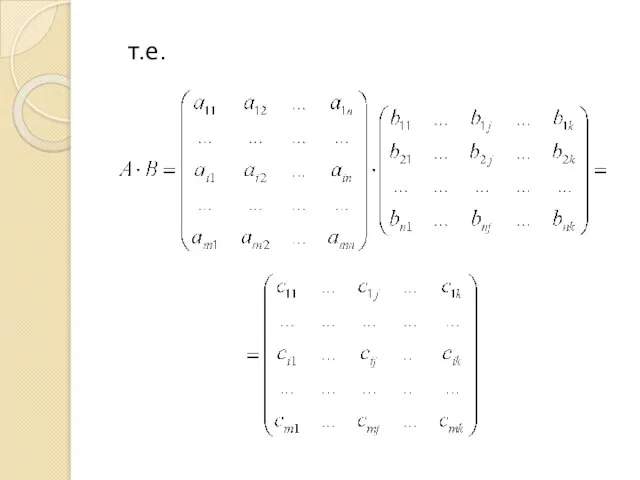
- 19. т.е.
- 20. Элементы матрицы С вычисляются по формуле: , т.е. каждый элемент равен сумме произведений элементов i-й строки
- 21. Пример. Вычислить произведение матриц А ∙ В, где Найдем размер матрицы-произведения
- 22. 5) Возведение в степень Определение. Целой положительной степенью Ат (т>1) только квадратной матрицы А называется произведение
- 23. Пример. Возвести матрицу A в квадрат и в куб, Решение.
- 24. 6) Транспонирование матрицы - переход от матрицы А к матрице , в которой строки и столбцы
- 25. Например, если , то . Свойства операции транспонирования:
- 26. 4. Свойства операций над матрицами Многие свойства, присущие операциям над числами, справедливы и для операций над
- 27. Однако имеются и специфические свойства матриц. Если произведение матриц А·В существует, то после перестановки сомножителей местами
- 28. 2) Если даже произведения А·В и В·А существуют, то они могут быть матрицами разных размеров. Пример.
- 29. 3) Когда оба произведения А·В и В·А существуют и оба – матрицы одинакового размера, коммутативный (переместительный)
- 30. Частный случай. Коммутативным законом обладает произведение любой квадратной матрицы А п-го порядка на единичную матрицу того
- 31. 4) Произведение двух ненулевых матриц может равняться нулевой матрице, т.е. из того, что А·В = О,
- 32. САМОСТОЯТЕЛЬНАЯ РАБОТА №1 Даны матрицы
- 33. Найти: 1) 2А-5В; 2) АВ; 3) ВА; 4) АВ+ВА; 5)
- 35. Скачать презентацию





























 Сложение дробей с одинаковым знаменателем. Урок 107
Сложение дробей с одинаковым знаменателем. Урок 107 Задание на исследование функции с помощью производной. ЕГЭ. Задание В14
Задание на исследование функции с помощью производной. ЕГЭ. Задание В14 Интерполяция. Графический способ интерполяции
Интерполяция. Графический способ интерполяции Учитель начальных классов Некрасова Елена Юрьевна Санкт-Петербург 2009-2010 уч.год
Учитель начальных классов Некрасова Елена Юрьевна Санкт-Петербург 2009-2010 уч.год Законы сложения
Законы сложения Название компонентов и результата деления
Название компонентов и результата деления Презентация на тему Площадь трапеции
Презентация на тему Площадь трапеции  Сумма углов треугольника (урок геометрии в 7 классе) Автор: Леонова Татьяна Ивановна, учитель математики МОУ «Лицей №7», г. С
Сумма углов треугольника (урок геометрии в 7 классе) Автор: Леонова Татьяна Ивановна, учитель математики МОУ «Лицей №7», г. С Дифференциальные уравнения высших порядков. Приложения дифференциальных уравнений в экономике. Лекция №15
Дифференциальные уравнения высших порядков. Приложения дифференциальных уравнений в экономике. Лекция №15 Презентация по математике "Графический способ решения уравнений" - скачать
Презентация по математике "Графический способ решения уравнений" - скачать  Сложение и вычитание смешанных чисел. 5 класс
Сложение и вычитание смешанных чисел. 5 класс Табличное сложение и вычитание
Табличное сложение и вычитание Дроби. Нахождение части числа
Дроби. Нахождение части числа Открытый урок алгебры в 8 классе по теме: Открытый урок алгебры в 8 классе по теме: «Квадратный трехчлен» (урок применения зн
Открытый урок алгебры в 8 классе по теме: Открытый урок алгебры в 8 классе по теме: «Квадратный трехчлен» (урок применения зн Взаимное положение прямых в пространстве
Взаимное положение прямых в пространстве Исследовательская работа по теме: «Конус и его применение в быту»
Исследовательская работа по теме: «Конус и его применение в быту» Масштаб, пропорции, проценты 6 класс
Масштаб, пропорции, проценты 6 класс Как люди научились считать
Как люди научились считать Объем тела. Принцип Кавальери
Объем тела. Принцип Кавальери Презентация по математике "Астрономические координаты" - скачать
Презентация по математике "Астрономические координаты" - скачать  Сравнение десятичных дробей
Сравнение десятичных дробей Простейшие комбинаторные задачи
Простейшие комбинаторные задачи Презентация на тему Измерение отрезков
Презентация на тему Измерение отрезков  Тренажёр по математике 1 класс. «Кот Леопальд на прогулке». Сложение и вычитание в пределах 10
Тренажёр по математике 1 класс. «Кот Леопальд на прогулке». Сложение и вычитание в пределах 10 Многогранники. Призма
Многогранники. Призма Отрезок. Измерение отрезков. Решение задач. Геометрия 7 класс
Отрезок. Измерение отрезков. Решение задач. Геометрия 7 класс Інтерполяційні методи наближення функцій однієї змінної
Інтерполяційні методи наближення функцій однієї змінної Сложение десятичных дробей
Сложение десятичных дробей