Содержание
- 2. Graphs and Multigraphs A graph G consists of two things: (i) A set V = V(G)
- 3. Graphs and Multigraphs Vertices u and v are said to be adjacent or neighbors if there
- 4. Multigraphs Consider the diagram on the left. The edges e4 and e5 are called multiple edges
- 5. Degree of a Vertex The degree of a vertex v in a graph G, written deg
- 6. Degree of a Vertex Theorem 8.1 also holds for multigraphs where a loop is counted twice
- 7. Finite Graphs, Trivial Graphs A multigraph is said to be finite if it has a finite
- 8. SUBGRAPHS, ISOMORPHICAND HOMEOMORPHIC GRAPHS Subgraphs Consider a graph G = G(V,E).Agraph H = H(V’,E’) is called
- 9. Isomorphic Graphs Graphs G(V,E) and G*(V*,E*) are said to be isomorphic if there exists a one-to-one
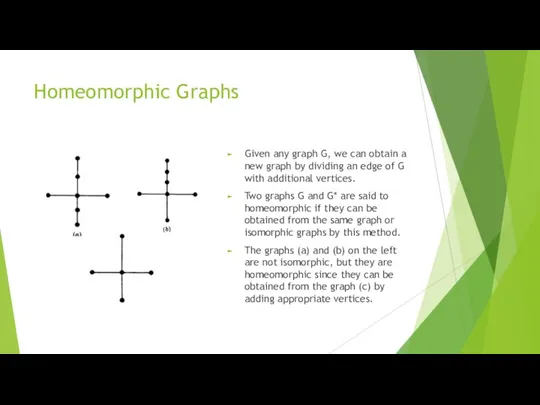
- 10. Homeomorphic Graphs Given any graph G, we can obtain a new graph by dividing an edge
- 11. PATHS
- 12. Paths Consider the following sequences: α = (P4,P1,P2,P5,P1,P2,P3, P6) β = (P4,P1,P5,P2,P6) γ = (P4,P1,P5,P2,P3,P5,P6) The
- 13. Connectivity/Connected Components A graph G is connected if there is a path between any two of
- 14. Distance and Diameter Consider a connected graph G. The distance between vertices u and v in
- 15. Cutpoints and Bridges Let G be a connected graph. A vertex v in G is called
- 16. TRAVERSABLE AND EULERIAN GRAPHS A multigraph is said to be traversable if it “can be drawn
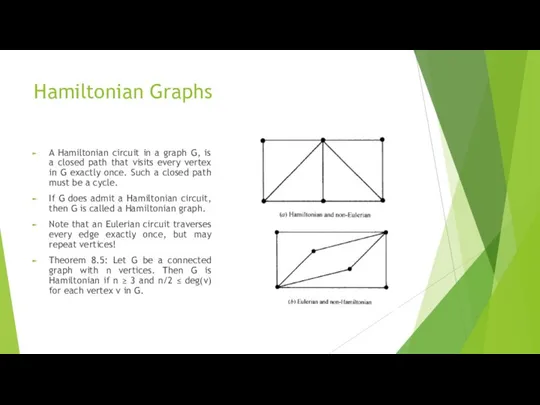
- 17. Hamiltonian Graphs A Hamiltonian circuit in a graph G, is a closed path that visits every
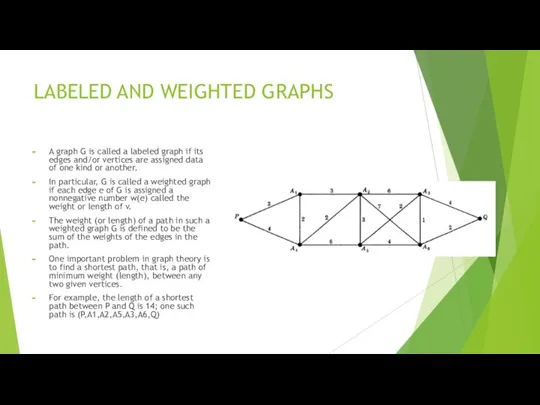
- 18. LABELED AND WEIGHTED GRAPHS A graph G is called a labeled graph if its edges and/or
- 19. COMPLETE, REGULAR,AND BIPARTITE GRAPHS A graph G is said to be complete if every vertex in
- 20. Trees A graph T is called a tree if T is connected and T has no
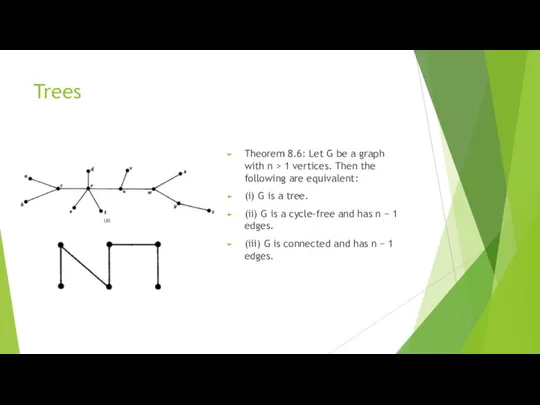
- 21. Trees Theorem 8.6: Let G be a graph with n > 1 vertices. Then the following
- 22. Spanning Trees A subgraph T of a connected graph G is called a spanning tree of
- 23. Minimal Spanning Trees Suppose G is a connected weighted graph. That is, each edge of G
- 24. Minimal Spanning Trees Example: Find a minimal spanning tree of the weighted graph Q. Note that
- 25. First we order the edges by decreasing weights, and then we successively delete edges without disconnecting
- 26. Minimal Spanning Trees Example: Find a minimal spanning tree of the weighted graph Q. Note that
- 27. First we order the edges by increasing weights, and then we successively add edges without forming
- 28. Planar Graphs A graph or multigraph which can be drawn in the plane so that its
- 29. Maps, Regions A particular planar representation of a finite planar multigraph is called a map. We
- 30. Maps, Regions Theorem 8.7: The sum of the degrees of the regions of a map is
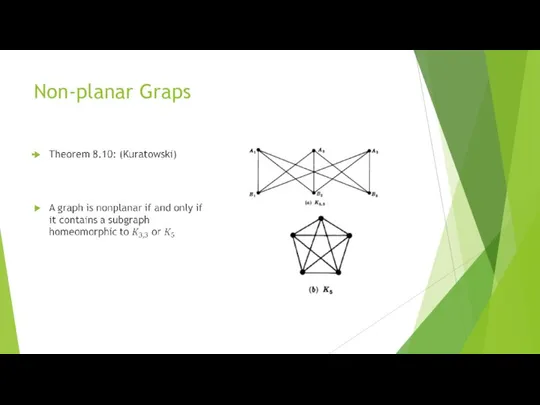
- 31. Non-planar Graps
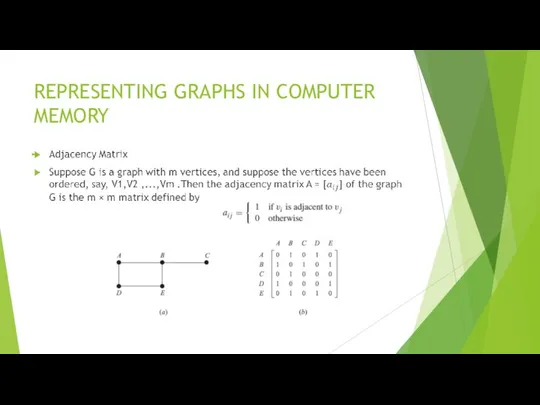
- 32. REPRESENTING GRAPHS IN COMPUTER MEMORY
- 33. REPRESENTING GRAPHS IN COMPUTER MEMORY
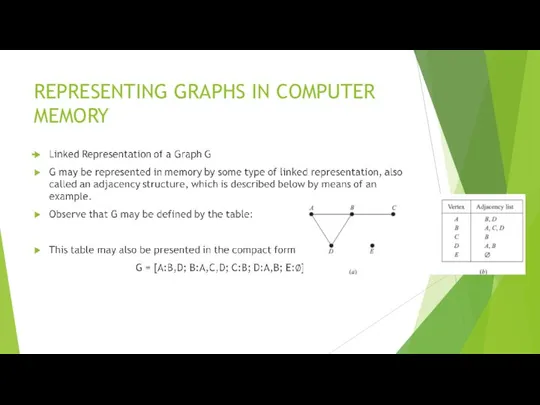
- 34. REPRESENTING GRAPHS IN COMPUTER MEMORY The linked representation of a graph G, which maintains G in
- 35. REPRESENTING GRAPHS IN COMPUTER MEMORY Edge File: The Edge File contains the edges of the graph
- 36. REPRESENTING GRAPHS IN COMPUTER MEMORY
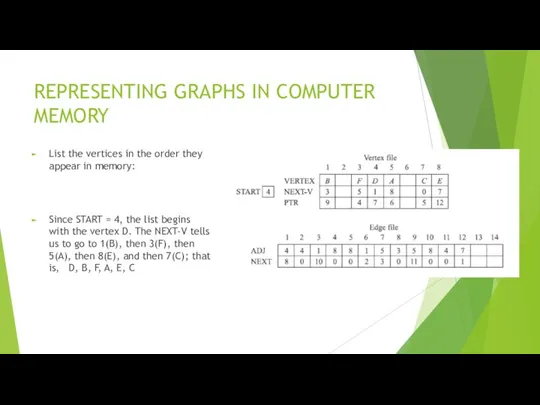
- 37. REPRESENTING GRAPHS IN COMPUTER MEMORY List the vertices in the order they appear in memory: Since
- 38. REPRESENTING GRAPHS IN COMPUTER MEMORY Find the adjacency list adj(v) of each vertex v of G
- 39. GRAPH ALGORITHMS This section discusses two important graph algorithms which systematically examine the vertices and edges
- 40. GRAPH ALGORITHMS During the execution of our algorithms, each vertex (node) N of G will be
- 41. DFS The general idea behind a depth-first search beginning at a starting vertex A is as
- 42. DFS
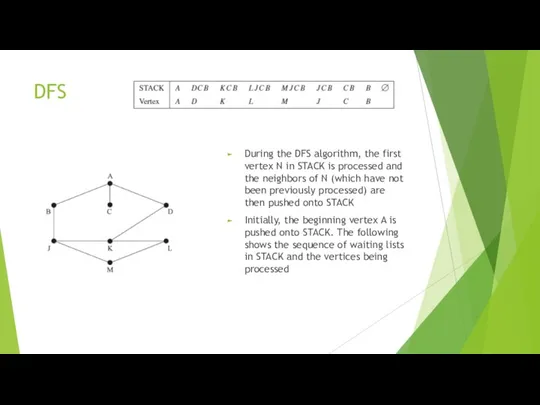
- 43. DFS During the DFS algorithm, the first vertex N in STACK is processed and the neighbors
- 44. BFS The general idea behind a breadth-first search beginning at a starting vertex A is as
- 45. BFS
- 46. BFS
- 47. Traveling Salesman Problem Let G be a complete weighted graph. (We view the vertices of G
- 48. Traveling Salesman Problem Consider the complete weighted graph G in Fig. 8-35(a). It has four vertices,
- 49. Traveling Salesman Problem We solved the “traveling-salesman problem” for the weighted complete graph by listing and
- 50. Traveling Salesman Problem Starting at P, the first row of the table shows us that the
- 51. Traveling Salesman Problem Starting at Q, the closest vertex is R with distance 11; from R
- 53. Скачать презентацию









































 Систематическая погрешность
Систематическая погрешность Презентация на тему ЛУЧ И УГОЛ
Презентация на тему ЛУЧ И УГОЛ  Історія розвитку комбінаторики та деякі її застосування
Історія розвитку комбінаторики та деякі її застосування Скалярное произведение векторов
Скалярное произведение векторов Математика 2 класс Урок разработан учителем начальных классов МОУ «СОШ №48» Крыцыной Еленой Анатольевной
Математика 2 класс Урок разработан учителем начальных классов МОУ «СОШ №48» Крыцыной Еленой Анатольевной Формулы приведения
Формулы приведения Предмет стереометрии. Аксиомы стереометрии
Предмет стереометрии. Аксиомы стереометрии Тема урока. Сложение и вычитание дробей с одинаковыми знаменателями.
Тема урока. Сложение и вычитание дробей с одинаковыми знаменателями. Длина окружности и площадь круга. 6 класс
Длина окружности и площадь круга. 6 класс Задание 2. Задача минимизировать время сбора утром на работу и в школу семьи из трех человек: отец, сын (10 лет), дочь (6 лет)
Задание 2. Задача минимизировать время сбора утром на работу и в школу семьи из трех человек: отец, сын (10 лет), дочь (6 лет) Как показать ученикам, что не всякая формула задает функцию и не всякую функцию можно задать формулой?
Как показать ученикам, что не всякая формула задает функцию и не всякую функцию можно задать формулой? Порядок выполнения действий
Порядок выполнения действий Умножение и деление чисел. Повторение
Умножение и деление чисел. Повторение Симметрия в пространстве
Симметрия в пространстве Симметрия. Центральная и осевая симметрии
Симметрия. Центральная и осевая симметрии Отношение двух чисел
Отношение двух чисел Презентация по математике "Рациональные уравнения" - скачать бесплатно
Презентация по математике "Рациональные уравнения" - скачать бесплатно Предварительный эксперимент и методы его анализа
Предварительный эксперимент и методы его анализа Задачи на движение. Математические модели
Задачи на движение. Математические модели Площадь параллелограмма
Площадь параллелограмма Решение задач на прямую и обратную пропорциональные зависимости
Решение задач на прямую и обратную пропорциональные зависимости Измерение физических величин и единицы их измерения
Измерение физических величин и единицы их измерения Тела Архимеда
Тела Архимеда Множество. Подмножество
Множество. Подмножество Доли и части от числа
Доли и части от числа Тригонометрические уравнения Практикум по решению и составлению тригонометрических уравнений
Тригонометрические уравнения Практикум по решению и составлению тригонометрических уравнений Алғашқы функция және интеграл
Алғашқы функция және интеграл Занимательная математика
Занимательная математика