Содержание
- 2. Теория алгоритмов Восходит к Давиду Гильберту На рубеже 20 века сформулировал мировую проблему: Можно ли построить
- 3. Типы алгоритмов. История создания Интенсивный поиск универсального уточнения алгоритма предложил примерно 20 формальных конструкций алгоритмов, которые
- 4. Алгоритмические машины (АМ) имеют единственный процессор, выполняющий небольшой набор очень примитивных действий, простую структуру данных (структуру
- 5. Основные АМ Машина Тьюринга (МТ) предложена Тьюрингом в 1937 г. Машина Поста (МР) предложена Постом в
- 6. Машина Тьюринга -абстрактный исполнитель (абстрактная вычислительная машина). Была предложена Аланом Тьюрингом в 1936 году для формализации
- 7. Автор ТЬЮРИНГ Алан Матисон (Turing Alan Mathison) (1912—1954), английский математик. Основные труды по математической логике, вычислительной
- 8. Соглашение об алгоритме
- 10. Структура алгоритма (составляющие алгоритма) Процессорная структура. (Исполнитель алгоритма). Во всех теоретических конструкциях алгоритмов и большинстве алгоритмических
- 11. Составляющие структуры Информационная структура алгоритма (ИСА). Структура функций есть описание конструирования функции от функций из базовых.
- 12. Интерпретация МТ. Процессор – в МТ называется управляющей головкой (УГ). Структура данных (память процессора) бесконечная лента,
- 13. МТ Тьюринг назвал свое абстрактное механическое устройство "универсальной машиной", поскольку она должна была справляться с любой
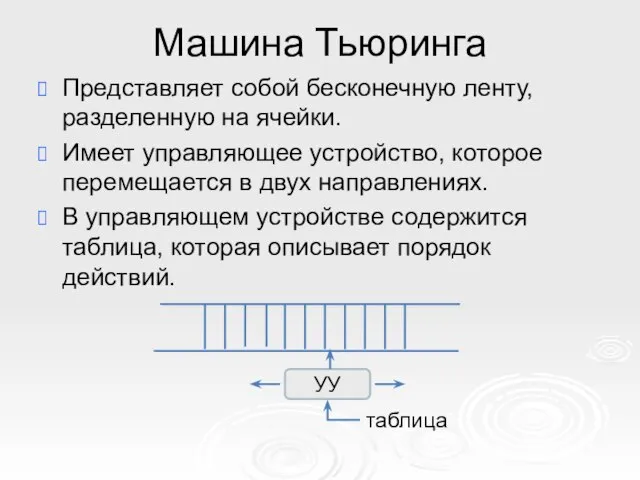
- 14. УУ таблица Машина Тьюринга Представляет собой бесконечную ленту, разделенную на ячейки. Имеет управляющее устройство, которое перемещается
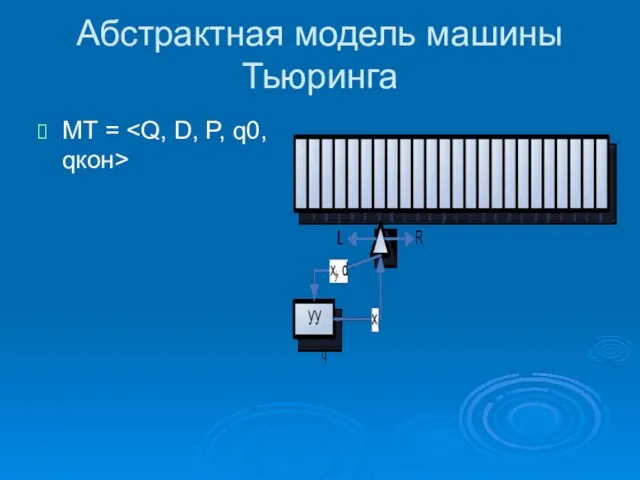
- 15. Абстрактная модель машины Тьюринга МТ =
- 16. МТ =
- 19. Машина Тьюринга состоит из трех частей: ленты, считывающе-записывающей головки и логического устройства Лента выступает в качестве
- 20. Головка неподвижна, а лента передвигается относительно нее вправо или влево. Машина работает в некотором произвольном конечном
- 21. В каждую ячейку ленты может быть записан лишь один символ. Информация, хранящаяся на ленте, изображается конечной
- 22. Система исполняемых головкой команд предельно проста: на каждом такте она производит замену символа в обозреваемой ячейке
- 23. Команды перемещений ленты L («Left») на ячейку влево, R («Right») на ячейку вправо S («Stop») остаться
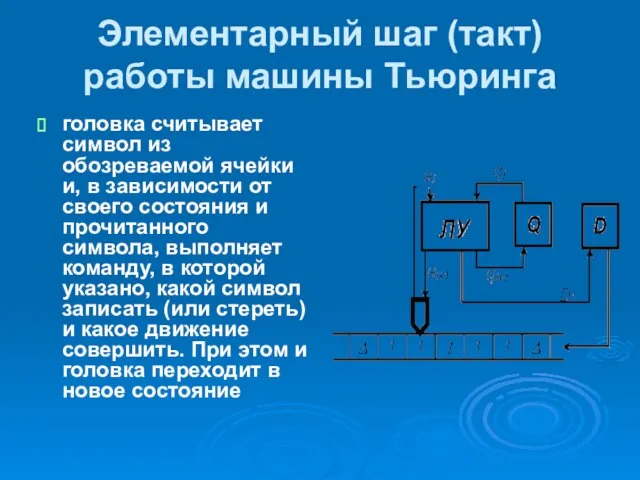
- 24. Элементарный шаг (такт) работы машины Тьюринга головка считывает символ из обозреваемой ячейки и, в зависимости от
- 25. Определение Конфигурация машины- совокупность состояний всех ячеек ленты, состояния УУ и положение головки В зависимости от
- 26. Пример Пусть начальной является конфигурация 1q11111. Такт 1 Обозревается 1, в ЛУ состояние q. Выходная команда
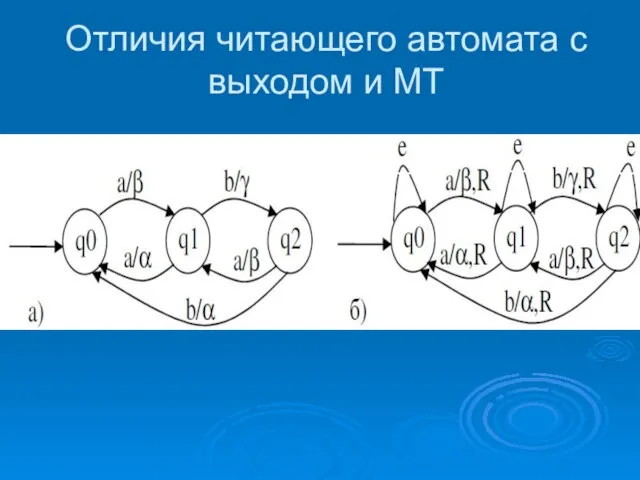
- 27. Отличия читающего автомата с выходом и МТ
- 28. Тезис Тьюринга Всякий алгоритм может быть задан посредством тьюринговой функциональной схемы и реализован в соответствующей машине
- 29. Отличия ЭВМ и машины Тьюринга Главное отличие машины Тьюринга от ЭВМ – бесконечная лента В отличие
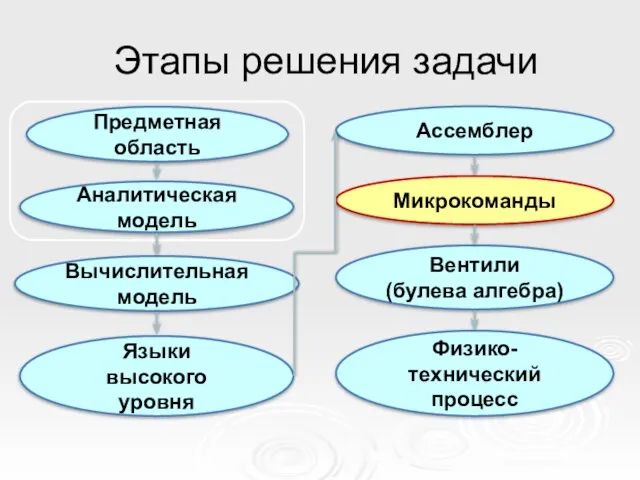
- 30. Языки высокого уровня Вычислительная модель Вентили (булева алгебра) Микрокоманды Предметная область Ассемблер Аналитическая модель Физико-технический процесс
- 31. Представление машины Тьюринга совокупностью команд Совокупность всех команд, которые может выполнять машина, называется ее программой. Машина
- 32. В качестве примера рассмотрим совокупность команд машины Тьюринга, которая инвертирует входную цепочку, записанную с использованием нулей
- 33. Представление машины Тьюринга графом При представлении машины Тьюринга посредством графа необходимо каждому состоянию поставить в соответствие
- 34. Представление машины Тьюринга таблицей соответствия
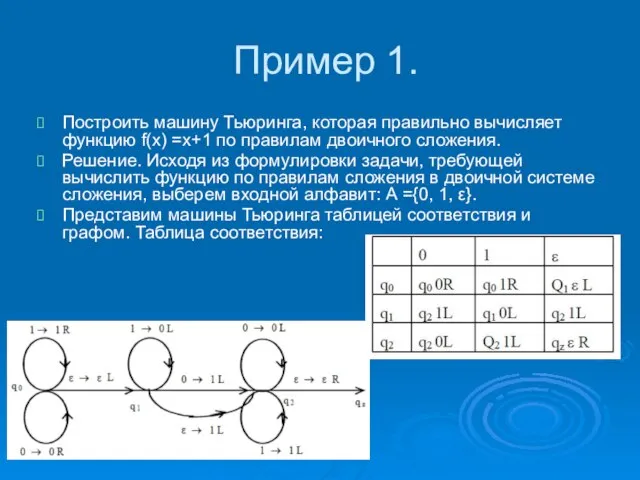
- 36. Пример 1. Построить машину Тьюринга, которая правильно вычисляет функцию f(x) =x+1 по правилам двоичного сложения. Решение.
- 37. Запишем программу построенной машины Тьюринга для случая, когда входная цепочка на ленте равна двоичному числу 111.
- 39. Построение МТ Для того чтобы доказать вычислимость функции, а в дальнейшем и существование алгоритма необходимо построить
- 40. Операции над машинами Тьюринга 1. Композиция машин Тьюринга. Пусть машины Т1 и Т2 имеют программы Р1
- 41. Пусть a01 = a02 = a0 и a11 = a12 = a1. Внешний алфавит композиции Т1Т2
- 42. Операции над МТ
- 43. Алгоритмическая машина Поста (МП) — абстрактная вычислительная машина, предложенная Эмилем Леоном Постом (Emil L. Post), которая
- 44. За один такт (его называют шагом) головка может сдвинуться на одну секцию вправо или влево и
- 45. Структура команды Каждая команда имеет следующую структуру xKy, x – номер исполняемой команды; K – указание
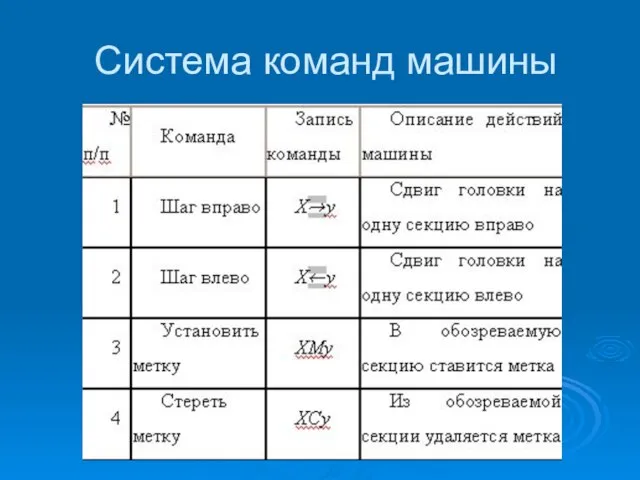
- 46. Система команд машины
- 47. Система команд машины
- 48. Пример
- 49. Комментарий к примеру Последовательное исполнение команд 1 и 2 приводит к тому, что головка за два
- 50. Если данные условия не выполняются, происходит безрезультатная остановка машины, т.е. остановка до получения запланированного результата. В
- 51. Функции, вычислимые алгоритмом алгоритм не определяется формально, а существует как бы в виде «всем понятной механической
- 52. Вычислимые функции Говорят, что машина Тьюринга вычисляет функцию f(x1, x2, ..., xn), если выполняются следующие условия:
- 56. Рекурсивные функции Рекурсивные функции на множестве натуральных чисел были предложены Клини в 1938 г. Конструктивные механизмы
- 57. Рекурсия Пример: определение факториала. n!=1*2*3*...*n. Н.Вирт отмечает, что "...мощность рекурсии связана с тем, что она позволяет
- 58. Рекурсивные функции Рекурси́вная фу́нкция (от лат. recursio — возвращение) — это числовая функция числового аргумента, которая
- 59. Свойства рекурсивных алгоритмов: Правильный рекурсивный алгоритм не должен создавать бесконечную последовательность вызовов самого себя. Для этого
- 60. Примитивная рекурсия Оператор примитивной рекурсии Rn позволяет определить (n+1) - местную функцию f по двум заданным
- 62. Тезис Чёрча — Тьюринга и алгоритмически неразрешимые проблемы Алан Тьюринг высказал предположение (известное как Тезис Чёрча
- 63. Исчисления. Исчисление функций, вычисляемых на множестве натуральных чисел предложено Эрбраном и Гёделем в 1938 г. λ-исчисление
- 64. Лямбда-исчисление Ля́мбда-исчисле́ние (λ-исчисление) — формальная система, разработанная американским математиком Алонзо Чёрчем, для формализации и анализа понятия
- 65. Метапрограммирование Метапрограммирование предусматривает написание программ, которые работают с другими программами в качестве данных. Язык обрабатывающей программы
- 66. Ассоциативное исчисление
- 70. Скачать презентацию




























































 Определители и их применения
Определители и их применения Текстовые задачи и пути их решения. Элективный курс. 9 класс
Текстовые задачи и пути их решения. Элективный курс. 9 класс Математика в профессии сварщика
Математика в профессии сварщика Комплексные числа
Комплексные числа Построение треугольников по заданным элемента
Построение треугольников по заданным элемента Расчет площадей помещений. (Лекция 9.7)
Расчет площадей помещений. (Лекция 9.7) Векторная алгебра
Векторная алгебра Презентация по математике "Урок математики. 2 класс." - скачать бесплатно
Презентация по математике "Урок математики. 2 класс." - скачать бесплатно Устный счет
Устный счет Тема: Порядок выполнения действий в выражениях без скобок. Цель: совершенствование знаний выполнения действий в выражениях без
Тема: Порядок выполнения действий в выражениях без скобок. Цель: совершенствование знаний выполнения действий в выражениях без  Вычитание чисел 5,6,7,8,9. Уменьшаемое, вычитаемое, разность
Вычитание чисел 5,6,7,8,9. Уменьшаемое, вычитаемое, разность Аппроксимация функций (тема 8)
Аппроксимация функций (тема 8) Мода и медиана
Мода и медиана Справочник по геометрии
Справочник по геометрии Презентация по математике "Графическое решение квадратных уравнений" - скачать
Презентация по математике "Графическое решение квадратных уравнений" - скачать  Связь между координатами вектора и координатами его начала и конца
Связь между координатами вектора и координатами его начала и конца Примеры на действия с алгебраическими дробями
Примеры на действия с алгебраическими дробями Целое уравнение и его корни. 9 класс
Целое уравнение и его корни. 9 класс Это мы не проходили… интеллектуально-познавательная игра
Это мы не проходили… интеллектуально-познавательная игра Аттестационная работа. Рациональные способы устных вычислений
Аттестационная работа. Рациональные способы устных вычислений Простейшие вероятностные задачи. Элементарные и сложные события. Вероятность противоположного события. (11 класс)
Простейшие вероятностные задачи. Элементарные и сложные события. Вероятность противоположного события. (11 класс) Презентация по математике "тренажер" - скачать бесплатно
Презентация по математике "тренажер" - скачать бесплатно Геометрия. Основные утверждения и теоремы
Геометрия. Основные утверждения и теоремы Математика. Закрепление
Математика. Закрепление Организация познавательной деятельности учащихся в условиях интеграции математики с физикой
Организация познавательной деятельности учащихся в условиях интеграции математики с физикой Презентация по математике "ЧИСЛО И ЦИФРА 5" - скачать бесплатно
Презентация по математике "ЧИСЛО И ЦИФРА 5" - скачать бесплатно Прибавление и вычитание числа 2 (Анимированная сорбонка)
Прибавление и вычитание числа 2 (Анимированная сорбонка) Презентация по математике "Окружность и круг" - скачать бесплатно
Презентация по математике "Окружность и круг" - скачать бесплатно