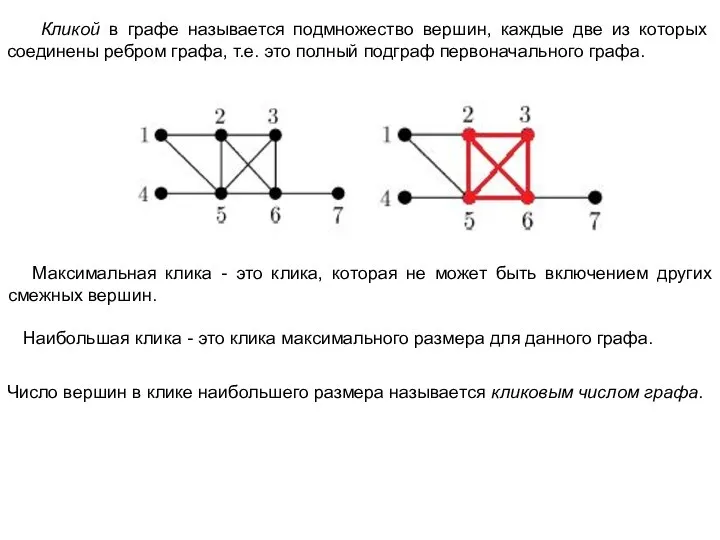
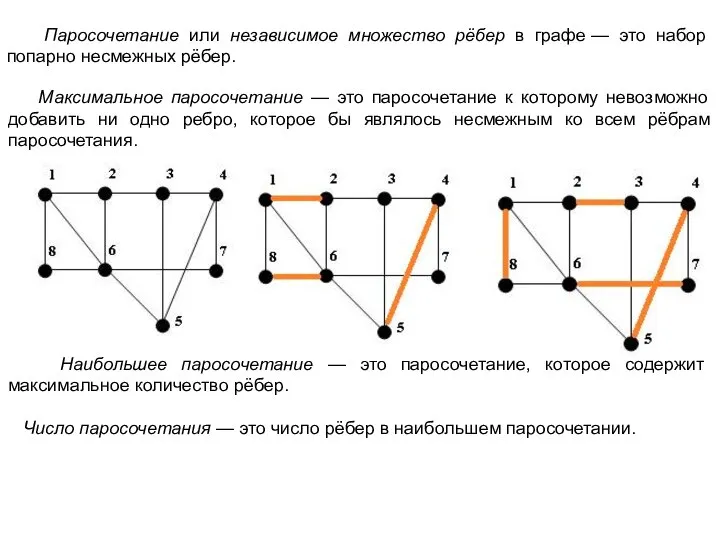
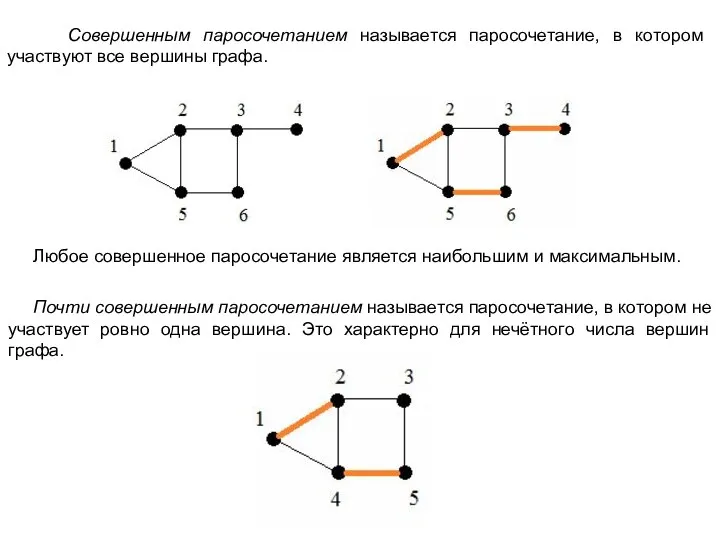
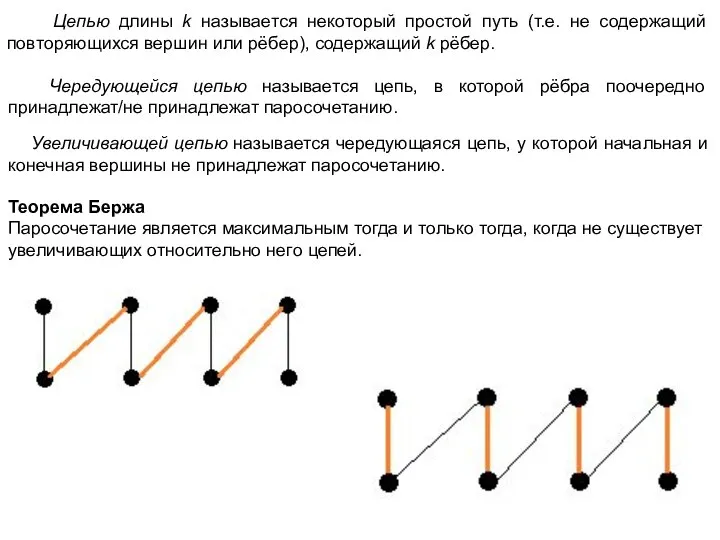
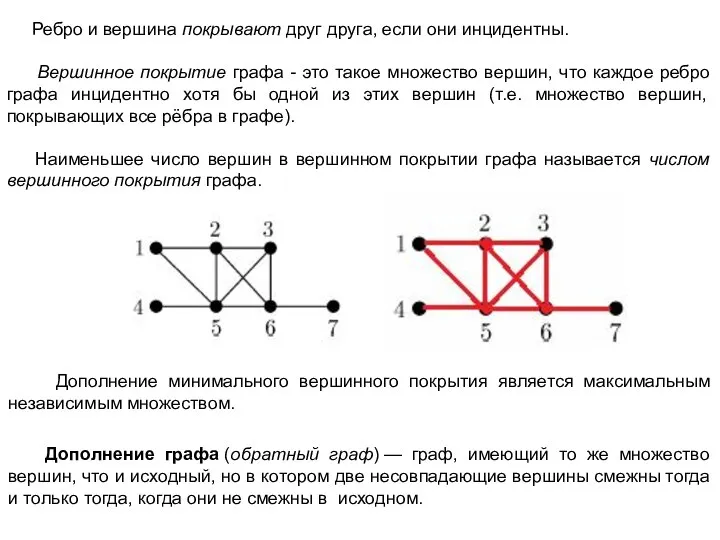
Алгоритм Брона - Кербоша – один из эффективных вариантов поиска клик.
Алгоритм основан на том, что клика в графе является его максимальным по включению полным подграфом. На каждом шаге, начиная с одной вершины в уже построенный полный подграф, добавляется вершина из множества кандидатов. При этом при переборе вершины, которые заведомо не приведут к построению клики отбрасываются.
Алгоритм Брона - Кербоша
Вход: G=(V, A) - неориентированный граф.
Выход: CL – клика.
Процедура ПОИСК(cand, notcand)
ПОКА cand != ∅ И notcand не содержит вершины, соединенной со всеми вершинами из cand
Выбираем v из cand и добавляем её в CL += v;
newcand = cand - все вершины, не соединенные с v;
newnotcand = notcand - все вершины, не соединенные с v;
ЕСЛИ newcand != ∅ и notcand != ∅ ТО
ВЫХОД;
ИНАЧЕ ПОИСК(newcand, notcand)
CL -= v; cand -= v; notcand += v.
Алгоритм АБК
CL={}; cand=V; notcand = {}; newcand = {}; newnotcand = {};
ПОИСК (cand, notcand)



 Ссора в царстве степенных функций
Ссора в царстве степенных функций Математическая викторина
Математическая викторина Призмы
Призмы Дискретная математика. Задание №6
Дискретная математика. Задание №6 Решение задач на комбинации многогранников и тел вращения
Решение задач на комбинации многогранников и тел вращения Модели, описываемые системами двух автономных дифференциальных уравнений
Модели, описываемые системами двух автономных дифференциальных уравнений Многоугольники
Многоугольники Коллекция задач. (6 класс)
Коллекция задач. (6 класс) Статистические гипотезы. Параметрические критерии. (Лекция 5)
Статистические гипотезы. Параметрические критерии. (Лекция 5) Презентация по математике "Комбинаторика. Комбинаторные задачи" - скачать бесплатно
Презентация по математике "Комбинаторика. Комбинаторные задачи" - скачать бесплатно Модуль числа
Модуль числа Нам радостно, нам весело! Смеемся мы с утра. Но вот пришло мгновенье, Серьезным быть пора. Глазки прикрыли, ручки сложили, Го
Нам радостно, нам весело! Смеемся мы с утра. Но вот пришло мгновенье, Серьезным быть пора. Глазки прикрыли, ручки сложили, Го Дом дружбы народов. II региональный турнир по ментальной арифметике. Ижевск 2018
Дом дружбы народов. II региональный турнир по ментальной арифметике. Ижевск 2018 Презентация по математике "ДЕСЯТОК. ДВУЗНАЧНЫЕ ЧИСЛА (1 КЛАСС)" - скачать бесплатно
Презентация по математике "ДЕСЯТОК. ДВУЗНАЧНЫЕ ЧИСЛА (1 КЛАСС)" - скачать бесплатно Виды треугольников: прямоугольный тупоугольный, остроугольный
Виды треугольников: прямоугольный тупоугольный, остроугольный Алгоритм. Свойства алгоритма
Алгоритм. Свойства алгоритма Сложение и вычитание векторов
Сложение и вычитание векторов Задачи на доли
Задачи на доли Вычитание векторов
Вычитание векторов Параллелограмм. Свойство параллелограмма
Параллелограмм. Свойство параллелограмма Алгебра логики. Логические операции
Алгебра логики. Логические операции Вертикальные углы
Вертикальные углы Многогранник с двумя основаниями
Многогранник с двумя основаниями Аттестационная работа. Элективный курс Теория чисел
Аттестационная работа. Элективный курс Теория чисел Деление с остатком
Деление с остатком Регрессионный анализ. Временные ряды
Регрессионный анализ. Временные ряды Симметрия топтары
Симметрия топтары Связь между числами при делении. Проверка деления
Связь между числами при делении. Проверка деления