- Главная
- Математика
- Основные понятия теории чисел. Лекция 9

Содержание
- 2. Обозначения: − N - множество натуральных чисел: целые положительные числа вида 1,2,…; − Z - множество
- 3. Лемма 4. Наименьший, отличный от единицы, делитель натурального числа n>1 есть простое число. Следствие. Каждое натуральное
- 4. Арифметика в классах вычетов Целые числа а и b (a,b∈z) называются сравнимыми по модулю n∈N (n≠0),
- 5. Алгоритм Евклида Алгоритм Евклида опирается на следующую теорему: для любого неотрицательного целого числа а и любого
- 6. Функция Эйлера обозначается символом ф(n) и представляет собой для каждого целого числа n, n>1, число положительных
- 7. Для простого р ф(p) = p - 1. Для произведения простых чисел р и q п
- 8. Альтернативная форма того же следствия: [mф(n)]k ≡ 1 mod n, mkф(n) ≡ 1 mod n, mkф(n)+1
- 9. Показатель числа a по модулю n Если a и n являются взаимно простыми ((a,n) = 1)
- 10. Степени целых чисел по модулю 19 А) Все последовательности заканчиваются числом 1. Б) Длина последовательности является
- 11. Если а является первообразным корнем n, его степени оказываются различными по модулю n и взаимно простыми
- 12. Дискретные логарифмы Известно, что любое целое число b можно представить в форме b ≡ r mod
- 14. Скачать презентацию
Обозначения:
− N - множество натуральных чисел: целые положительные числа вида
Обозначения:
− N - множество натуральных чисел: целые положительные числа вида
− Z - множество целых чисел: числа вида n, -n и 0, где n - натуральное число;
− Q - множество рациональных чисел: числа вида p/q, где p и q - целые числа и
.
Число а делится на число b
0, если существует число q такое, что
Число b - делитель числа а, число а - кратное числа b, число q - частное от деления а на b.
Утверждение о том, что b делит а обозначают символом
. Если b не делит а, то этот факт обозначают
.
Лемма 1. Если
и
, то
.
Лемма 2. Если m=a+b, d/m и d/a, то d/a.
Общим делителем двух или нескольких чисел называется число, являющееся делителем каждого из этих чисел.
Наибольшим общим делителем (НОД) чисел называется наибольший из их общих делителей - обозначается как
Число n>1 называется простым, если оно не имеет других делителей, кроме 1 и n.
Например, числа 2, 3, 5, 7 являются простыми, т.к. они делятся только на 1 и на самих себя.
Число n называется составным, если оно имеет делитель, отличный от 1 и n.
Например, числа 4, 6, 8 − составные числа.
Если НОД , то числа называют взаимно простыми.
Например: (2,5)=1; (10,21)=1.
Лемма 3. Если целое число b взаимно просто с каждым из целых чисел , то b взаимно просто с их произведением
Теорема о делении с остатком. Если а и b целые числа, и b>0, то существуют единственные целые числа q и r такие, что a=b x q+r,
Число q называют неполным частным при делении a на b, число r называют остатком от деления а на b.
Лемма 4. Наименьший, отличный от единицы, делитель натурального числа n>1 есть
Лемма 4. Наименьший, отличный от единицы, делитель натурального числа n>1 есть
Следствие. Каждое натуральное число n>1 имеет хотя бы один простой делитель.
Лемма 5. Если p - простое число, то любое целое число а либо взаимно простое с р, либо делится на р, т.е. р/а.
Основная теорема арифметики.
Любое натуральное число n>1 представляется в виде произведения простых чисел, причем, единственным образом.
Разложение числа n на простые сомножители:
Пусть p1,…,pк − различные из чисел p1,…,pr (r>k), a α1,…,αk − кратности, с которыми они входят в исходное разложение. Тогда это разложение можно записать в виде:
и называется оно каноническим разложением числа n на простые множители.
Пример.
Согласно теореме Евклида, множество простых чисел бесконечно.
Решето Эратосфена :
− напишем одно за другим числа 2,3,…N;
− число 2 является простым − оставляем, и зачеркиваем после него все числа, кратные 2, т.е. все четные числа;
− следующим за числом 2 является число 3, которое является простым. Оставляем 3, зачеркиваем все числа, кратные 3;
− продолжая этот процесс, находим все простые числа, не превышающие заданного числа N.
Например, N=40:
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40.
Простые числа:
2,3,5,7,11,13,17,19,23,29,31,37.
Особый класс простых чисел составляют числа вида
- простые числа Мерсенна
В 1992 г. найдено 32−е число Мерсенна (Его запись содержит 227 832 цифры и требует около ста страниц текста).
Длина десятичной записи предыдущего открытого числа была 9808358.
Арифметика в классах вычетов
Целые числа а и b (a,b∈z) называются сравнимыми
Арифметика в классах вычетов
Целые числа а и b (a,b∈z) называются сравнимыми
Сравнимость чисел a и b по модулю n обозначают символом
, называемым сравнением по модулю n.
Числа a и b сравнимы по модулю n тогда и только тогда, когда существует целое t(t∈z) такое, что
также и только тогда, когда они имеют одинаковые остатки r при делении на n, т.е. a = n q1 + r, b = n q2 + r.
Т.е. все целые числа Z по модулю n разбиваются по n непересекающихся классов сравнимых между собой чисел (т.е. имеющих одинаковые остатки при делении на n). Каждое число r, входящее в какой - либо из классов, называется вычетом числа a по модулю n, а каждый класс - классом вычетов по модулю n. Число разных классов вычетов равно n.
Полной системой вычетов (по модулю n или m) называют множество из m (или n) целых чисел
, если для любого целого числа a существует точно одно число
) из множества
такое, что
Свойства
сравнений по модулю m (или n) напоминают свойства обычных числовых равенств:
1. Два числа, сравнимые с третьим, сравнимы между собой.
2. Сравнения по одному и тому же модулю можно почленно складывать:
3. Сравнения по одному и тому же модулю можно почленно перемножать:
Правила сокращения сравнений несколько отличаются от правил сокращения равенств.
4. Если
Если
Пример, когда это условие не выполнено:
6
3 = 18
2 mod 8,
6
7 = 42
2 mod 8,
Однако, 3
7 mod 8.
Для произвольного модуля сравнения m (или n) в результате умножения чисел от 0 до (m - 1) на множитель а не получается полного набора всех вычетов,
Для произвольного модуля сравнения m (или n) в результате умножения чисел от 0 до (m - 1) на множитель а не получается полного набора всех вычетов, когда а и m имеют общие множители.
Алгоритм Евклида
Алгоритм Евклида опирается на следующую теорему:
для любого неотрицательного целого числа
Алгоритм Евклида
Алгоритм Евклида опирается на следующую теорему:
для любого неотрицательного целого числа
(a, b) = (b, a mod b). (9.2)
Чтобы определить наибольший общий делитель, равенство (9.2) можно использовать повторно.
В алгоритме Евклида многократно применяется равенство (9.2) для определения наибольшего общего делителя.
Пример. Чтобы найти (1970,1066), выполним следующие действия:
1970 = 1*1066 + 904 (1066,904)
1066 = 1*904+162 (904,162)
904 = 5*162+94 (162,94)
162 = 1*94+68 (94,68)
94 = 1*68+26 (68,26)
68 = 2*26+16 (26,16)
26 = 1*16+10 (16,10)
16 = 1*10+6 (10,6)
10 = 1*6+4 (6,4)
6 = 1*4+2 (4,2)
4 = 2*2+0 (2,0)
Следовательно, (1970,1066)=2.
Обобщенный алгоритм Евклида определяет:
1. наибольший общий делитель двух положительных целых чисел
и, если эти числа оказываются взаимно простыми,
2. мультипликативное обратное одного из них по модулю другого.
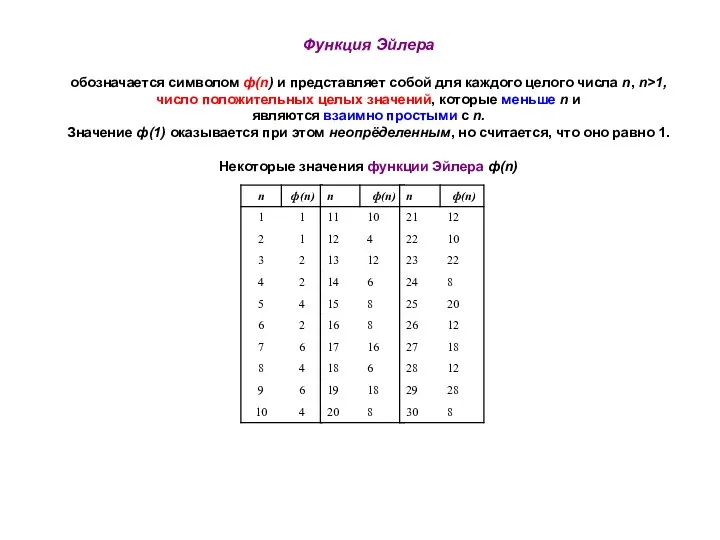
Функция Эйлера
обозначается символом ф(n) и представляет собой для каждого целого числа
Функция Эйлера
обозначается символом ф(n) и представляет собой для каждого целого числа
число положительных целых значений, которые меньше n и
являются взаимно простыми с n.
Значение ф(1) оказывается при этом неопрёделенным, но считается, что оно равно 1.
Некоторые значения функции Эйлера ф(n)
Для простого р
ф(p) = p - 1.
Для произведения простых чисел р
Для простого р
ф(p) = p - 1.
Для произведения простых чисел р
п = pq
получим:
ф(n) = ф(pq) = ф(p) x ф(p) = (p-1) x (q-1)
Доказательство.
Значениями, не являющимися взаимно простыми с п, будут значения множеств
{р, 2р, ... (q - 1)р} и {q, 2q, ..., (р - 1)q}, а также 0.
Соответственно
ф(п) = pq - [(q - 1) + (р - 1) + 1] =
= pq - (p + q) + 1 =
= (p-1) x (q-1) =
= ф(p) x ф(q).
Теорема Эйлера
Для любых взаимно простых чисел а и n (т.е. таких, что (a,n)=1)
Альтернативная формулировка теоремы:
Следствие для эффективности применения алгоритма RSA.
Для любых двух простых чисел р и q и чисел п = pq и т (здесь 0 < т < n) выполняется следующее условие:
Альтернативная форма того же следствия:
[mф(n)]k ≡ 1 mod n,
mkф(n) ≡ 1
Альтернативная форма того же следствия:
[mф(n)]k ≡ 1 mod n,
mkф(n) ≡ 1
mkф(n)+1 = mk(p-1)(q-1)+1 ≡ m mod n.
Из теоремы Эйлера следует малая теорема Ферма:
Если р - простое число и
, то
Тест Рабина
для проверки чисел на простоту
Пусть имеется число
N = 2S t + 1, где t - нечетно,
и требуется установить, простое оно или составное.
1. Выбирается случайное число 1 ≤а ≤ N и проверяются два условия:
1) N не делится на а;
2) аt = 1 (mod N) или существует целое k (0 ≤ k ≤s), для которого
2. Если оба условия выполняются, то вероятность того, что число N окажется составным, равна 1/4.
3. Если провести не один, a n аналогичных тестов, выбирая случайное а, то можно установить простоту числа с вероятностью 4 -n.
За счет выбора большого n можно добиться того, что вероятность ошибочного выбора простого числа для создания криптосистемы окажется ниже, чем вероятность ее взлома существующими методами (например, пробой на ключ).
Показатель числа a по модулю n
Если a и n являются взаимно
Показатель числа a по модулю n
Если a и n являются взаимно
удовлетворяющее соотношению
− это число
существование которого
Для наименьшего из положительных , при которых выполняется условие
порядок числа a по модулю n,
показатель, которому принадлежит a по модулю n,
длина периода последовательности, генерируемой степенями а.
Чтобы убедиться в истинности последнего пункта, рассмотрим степени числа 7 по модулю 19:
71 = 7 mod 19,
72 = 49 = 2*19 + 11 = 11 mod 19,
73 = 343 = 18*19 + 1 = 1 mod 19,
74 = 2401 = 126*19 + 7 = 7 mod 19,
75 = 16807 = 884*19 + 11 = 11 mod 19.
Последовательность является периодической с периодом, равным наименьшему положительному показателю n, при котором 7n = 1 (mod 19).
Наименьшее из чисел
называется показателем числа а по модулю n.
обеспечивается теоремой Эйлера.
Показатель числа а по модулю n является делителем числа ф(n).
В частном случае, когда показатель числа а по модулю n равен ф(n), (наивысший из показателей числа а по модулю n), то а называется первообразным (примитивным) корнем по модулю n.
используются также еще следующие названия:
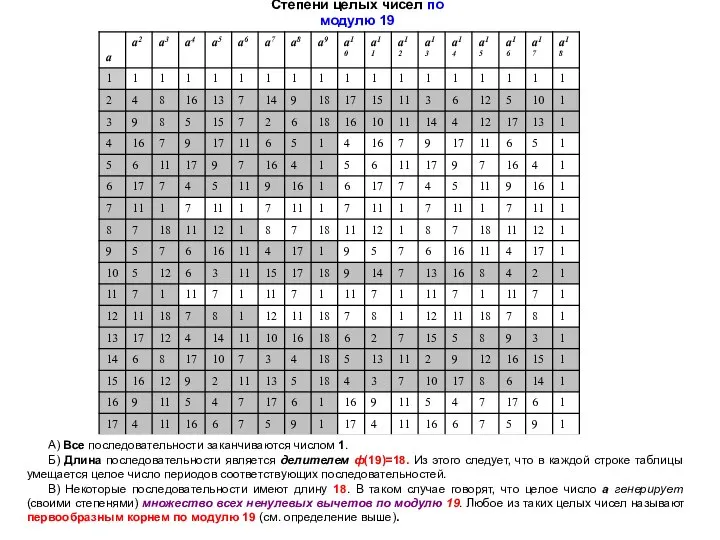
Степени целых чисел по модулю 19
А) Все последовательности заканчиваются числом 1.
Б)
Степени целых чисел по модулю 19
А) Все последовательности заканчиваются числом 1.
Б)
В) Некоторые последовательности имеют длину 18. В таком случае говорят, что целое число а генерирует (своими степенями) множество всех ненулевых вычетов по модулю 19. Любое из таких целых чисел называют первообразным корнем по модулю 19 (см. определение выше).
Если а является первообразным корнем n, его степени
оказываются различными по модулю
Если а является первообразным корнем n, его степени
оказываются различными по модулю
В частности, для простого числа р, если а является первообразным корнем р, то
оказываются различными по модулю р.
Для простого числа 19 его первообразными корнями являются числа
2, 3, 10, 13, 14 и 15.
Целыми числами с первообразными корнями будут только числа
2, 4, ра и 2ра ,
где р - любое нечетное простое число.
Дискретные логарифмы
Известно, что любое целое число b можно представить в
Дискретные логарифмы
Известно, что любое целое число b можно представить в
b ≡ r mod р , где 1 ≤ r ≤ (р - 1)
в классах вычетов.
Отсюда вытекает, что для любого целого числа b и любого первообразного корня а простого числа р можно найти ровно один показатель степени i, для которого
b ≡ ai mod р, где 1 ≤ i ≤ (р - 1).
Значение этого показателя называют
индексом числа b по модулю р при основании а.
Записывается это значение как ind a,p (b).
Свойства индексов чисел
ind a,p (1)= 0 , поскольку а0 mod р = 1 mod р = 1,
ind a,p (a)= 1, поскольку a1 mod р = а ,
ind a,p (xy)= [ind a,p (x)+ ind a,p (y)] mod ф(p),
ind a,p (yr)= [r ind a,p (y)] mod ф(p).
Из-за аналогии между обычными логарифмами и индексами последние называют
дискретными логарифмами.





![Альтернативная форма того же следствия: [mф(n)]k ≡ 1 mod n, mkф(n)](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1466709/slide-7.jpg)



 Проценты в нашей жизни Авторы: творческая группа «Одноклассники» - учащиеся 6 А класса. Руководитель проекта: Бирюко
Проценты в нашей жизни Авторы: творческая группа «Одноклассники» - учащиеся 6 А класса. Руководитель проекта: Бирюко Три проекции призмы. (Задача 62)
Три проекции призмы. (Задача 62) Взвешенные деревья
Взвешенные деревья Трапеция. Элементы трапеции
Трапеция. Элементы трапеции История развития тригонометрии
История развития тригонометрии Логика реляционная. Понятие реляционной модели
Логика реляционная. Понятие реляционной модели Двугранный угол. Решение задач. Трехгранный угол
Двугранный угол. Решение задач. Трехгранный угол «Проценты» 5 класс Учитель математики МБОУ СОШ № 11, г. Кропоткин Бутенко Елена Константиновна
«Проценты» 5 класс Учитель математики МБОУ СОШ № 11, г. Кропоткин Бутенко Елена Константиновна Второй признак равенства треугольников
Второй признак равенства треугольников Весь курс геометрии. (7 класс)
Весь курс геометрии. (7 класс) Доли. Обыкновенные дроби. (5 класс)
Доли. Обыкновенные дроби. (5 класс) Треугольник. Периметр
Треугольник. Периметр Основные показатели безотказности
Основные показатели безотказности Тренажёр по математике 1 класс. Кот Леопальд на прогулке. Сложение и вычитание в пределах 10
Тренажёр по математике 1 класс. Кот Леопальд на прогулке. Сложение и вычитание в пределах 10 Фестиваль исследовательских и творческих Фестиваль исследовательских и творческих работ учащихся «Портфолио» Автор: Дягилева
Фестиваль исследовательских и творческих Фестиваль исследовательских и творческих работ учащихся «Портфолио» Автор: Дягилева МС(К)ОУ «Большеусинская специальная (коррекционная) общеобразовательная школа-интернат 8 вида» Урок математики в 3 классе
МС(К)ОУ «Большеусинская специальная (коррекционная) общеобразовательная школа-интернат 8 вида» Урок математики в 3 классе  Geometrické osvětlení
Geometrické osvětlení Презентация по математике "Число 0" - скачать
Презентация по математике "Число 0" - скачать  Многогранники. Правильні многогранники
Многогранники. Правильні многогранники Площадь параллелограмма
Площадь параллелограмма Архимедовы тела. Каталановы тела
Архимедовы тела. Каталановы тела Урок - сказка Разработана Яковлевой Натальей Владимировной преподавателем ГОУ СПО «Валуйское медицинское училище» г. Валуйки
Урок - сказка Разработана Яковлевой Натальей Владимировной преподавателем ГОУ СПО «Валуйское медицинское училище» г. Валуйки  Наибольшее и наименьшее значения ФНП
Наибольшее и наименьшее значения ФНП Сумма векторов. Задания для устного счета. Упражнение 14
Сумма векторов. Задания для устного счета. Упражнение 14 Логарифмы. Определение
Логарифмы. Определение Деление десятичной дроби на натуральное число
Деление десятичной дроби на натуральное число Геометрический смысл производной
Геометрический смысл производной Аналитические функции и конформные отображения
Аналитические функции и конформные отображения