Содержание
- 2. Понятие производной Пусть y = f(x) есть непрерывная функция аргумента x, определенная в промежутке (a; b),
- 3. k = f ′(xo) = tg α – это угловой коэффициент касательной. f(xo) Касательная к графику
- 5. Приближенные вычисления f(x) ≈ f(xo) + f ′(xo)∆x (1) (2) (1 + ∆x)n ≈ 1 +
- 6. Общий вид уравнения касательной y = f ′(xo)(x – xo) + f(xo) Алгоритм составления уравнения касательной
- 7. Правила дифференцирования и таблица производных
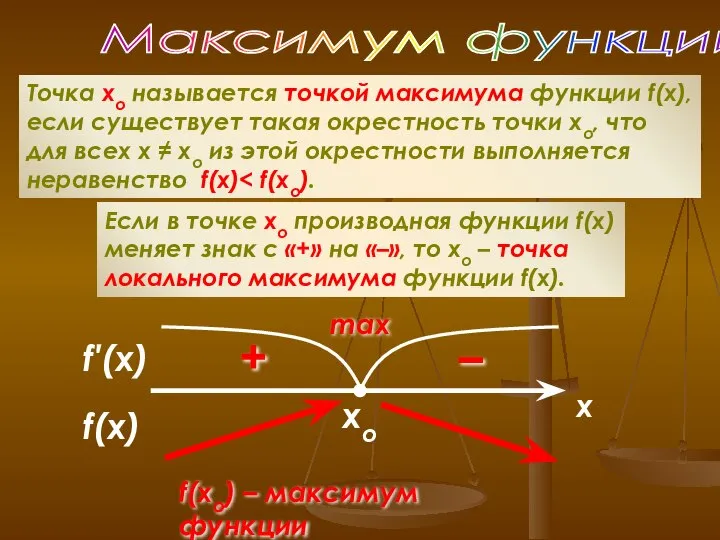
- 10. xo Максимум функции Точка хо называется точкой максимума функции f(x), если существует такая окрестность точки хо,
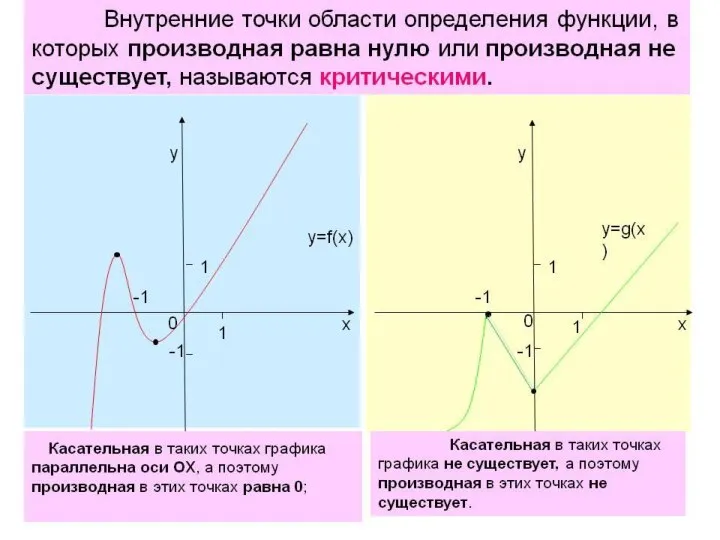
- 12. Теорема Дарбу. Точки, в которых производная функции равна 0 или не существует, делят область определения функции
- 13. Монотонность функций 1) Если f′(x) > 0 внутри промежутка I, то функция f возрастает на этом
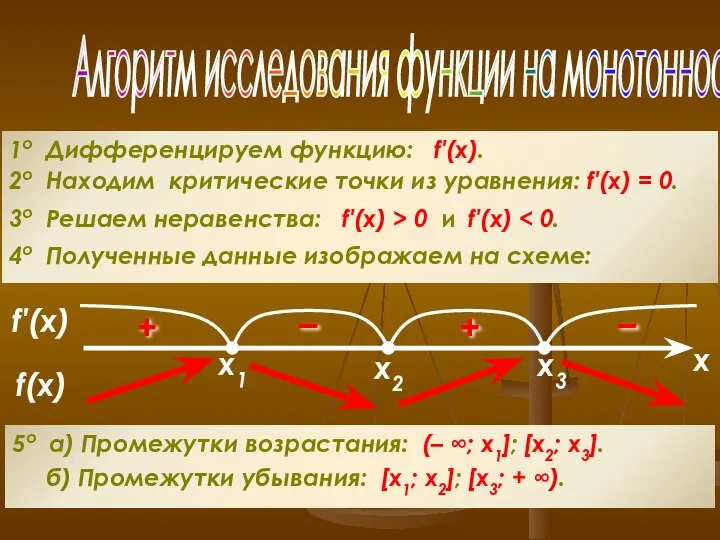
- 14. Алгоритм исследования функции на монотонность 1о Дифференцируем функцию: f′(x). 2о Находим критические точки из уравнения: f′(x)
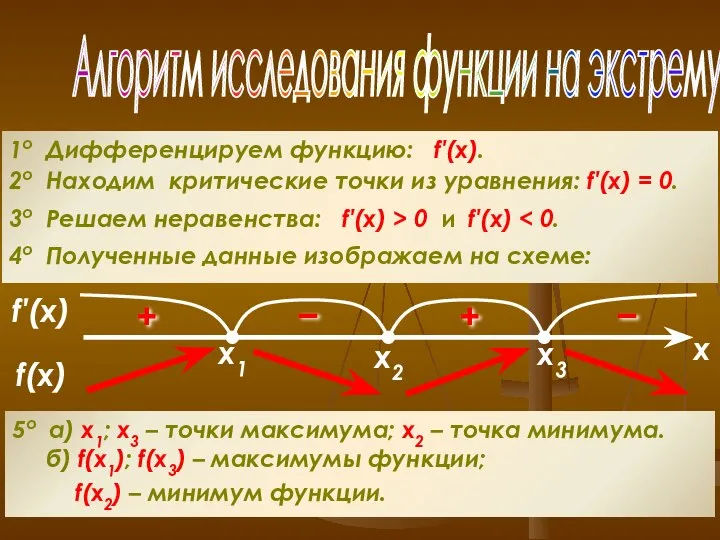
- 15. Алгоритм исследования функции на экстремумы 1о Дифференцируем функцию: f′(x). 2о Находим критические точки из уравнения: f′(x)
- 18. Скачать презентацию



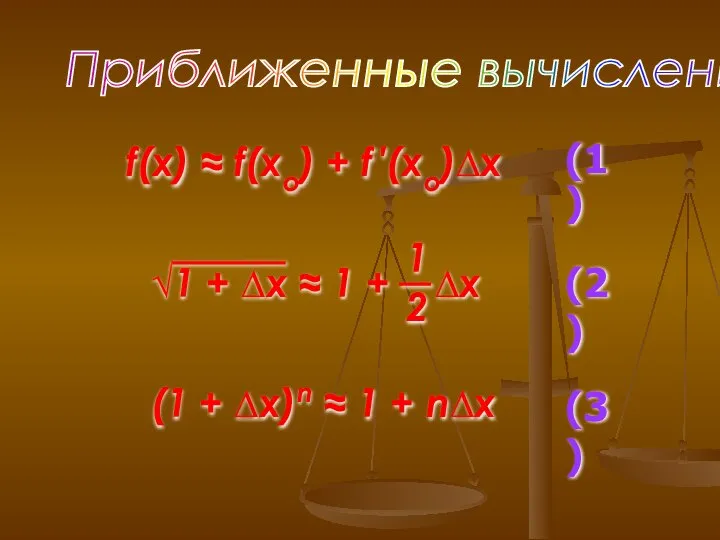







 Статистические таблицы
Статистические таблицы Для каждого графика укажите соответствующую формулу
Для каждого графика укажите соответствующую формулу «Проценты» 5 класс Учитель математики МБОУ СОШ № 11, г. Кропоткин Бутенко Елена Константиновна
«Проценты» 5 класс Учитель математики МБОУ СОШ № 11, г. Кропоткин Бутенко Елена Константиновна Математический турнир
Математический турнир Игра
Игра Арифметическая прогрессия
Арифметическая прогрессия Число и цифра 4
Число и цифра 4 Решение логарифмических уравнений и неравенств. Урок-соревнование по математике в 11 классе
Решение логарифмических уравнений и неравенств. Урок-соревнование по математике в 11 классе Закон звезды, или геометрические построения в орнаменте. Деление окружности
Закон звезды, или геометрические построения в орнаменте. Деление окружности Сложение и вычитание векторов
Сложение и вычитание векторов Перестановки, размещения, cочетания, вероятность
Перестановки, размещения, cочетания, вероятность Проверка умножения (3 класс)
Проверка умножения (3 класс) Поняття та призначення функцій
Поняття та призначення функцій Рефлексия. Графический диктант
Рефлексия. Графический диктант Сложение и вычитание в пределах 10
Сложение и вычитание в пределах 10 Готовимся к ГИА, 9 класс. Тест 4, часть 2
Готовимся к ГИА, 9 класс. Тест 4, часть 2 Функции и их свойства. (9 класс)
Функции и их свойства. (9 класс) Прямая и обратная пропорциональные зависимости
Прямая и обратная пропорциональные зависимости Определители второго и третьего порядка
Определители второго и третьего порядка Отношения. Решение задач
Отношения. Решение задач Теорема Виета. Устная работа. Проверка выполнения домашней работы
Теорема Виета. Устная работа. Проверка выполнения домашней работы Готовимся к ЕГЭ. Задания В 8 и В 14
Готовимся к ЕГЭ. Задания В 8 и В 14 Сложение и вычитание смешанных чисел. 5 класс
Сложение и вычитание смешанных чисел. 5 класс Презентация по теме: «Числа с собственными именами».
Презентация по теме: «Числа с собственными именами». Умножение смешанных чисел
Умножение смешанных чисел Однородная система линейных алгебраических уравнений. Фундаментальная система решений
Однородная система линейных алгебраических уравнений. Фундаментальная система решений Сумма углов треугольника. Внешний угол треугольника. Математический диктант
Сумма углов треугольника. Внешний угол треугольника. Математический диктант Модуль числа
Модуль числа