Содержание
- 2. χ2 -распределение Имея n независимых случайных величин х1, х2, …хn, при их нормально распределении можно получить
- 3. F-распределение Из нормального распределения генеральной совокупности взяли две выборки объемами n1 и n2 Cо степенями свободы
- 4. Распределение Пуассона Для представления функций от дискретных величин. Примеры – подсчет импульсов в радиохимии; подсчет квантов
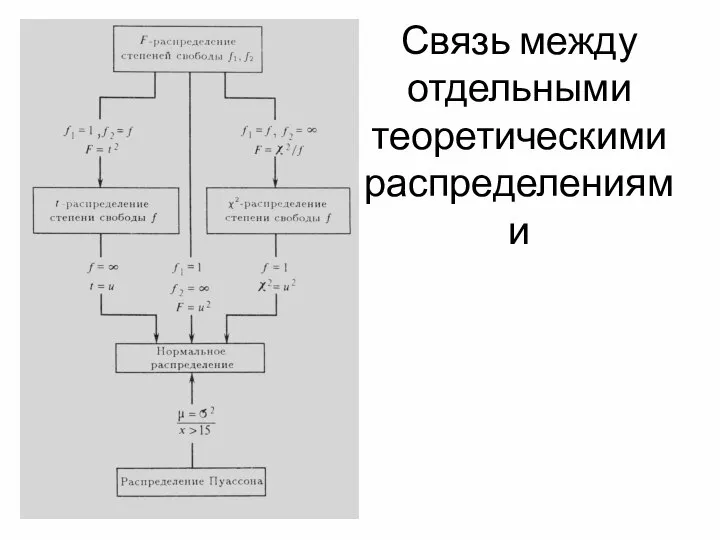
- 5. Связь между отдельными теоретическими распределениями
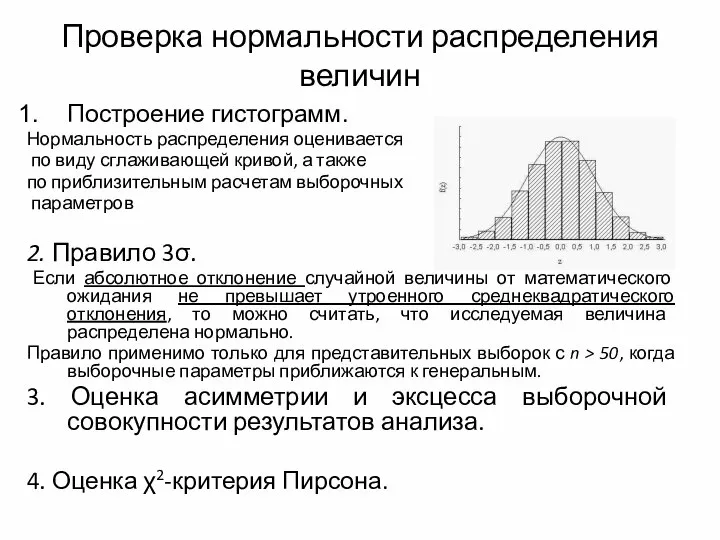
- 6. Проверка нормальности распределения величин Построение гистограмм. Нормальность распределения оценивается по виду сглаживающей кривой, а также по
- 7. Асимметрия При анализе вариационных рядов смещение от центра и крутизну распределения характеризуют специальные показатели. Асимметрия распределения
- 8. Асимметрия имеет место При межлабораторных опытахв несравнимых лабораториях, если результаты отдельных лабораторий имеют систематические ошибки с
- 9. Эксцесс Эксцесс служит для сравнения на «крутость» выборочного распределения с нормальным распределением. Распределение полученных результатов можно
- 10. Неравенство Чебышева Используется в тех случаях, когда распределение результатов и случайных ошибок анализа заведомо отличается от
- 12. Скачать презентацию







 Сложение векторов. Правило треугольника
Сложение векторов. Правило треугольника Обыкновенные дроби. 5 класс
Обыкновенные дроби. 5 класс Проект «Смоленские задачи»
Проект «Смоленские задачи» Отображение множеств
Отображение множеств Степень с натуральным показателем
Степень с натуральным показателем Аттестационная работа. Методы, способы мотивации в процессе обучения математике
Аттестационная работа. Методы, способы мотивации в процессе обучения математике Элементы теории бинарных отношений. Формы представления отношений. Операции над отношениями
Элементы теории бинарных отношений. Формы представления отношений. Операции над отношениями Сравнение десятичных дробей. 5 класс
Сравнение десятичных дробей. 5 класс Метод координат в пространстве. Урок № 4
Метод координат в пространстве. Урок № 4 Симметрии в технике
Симметрии в технике Координаты на плоскости. 6 класс
Координаты на плоскости. 6 класс Упрощение выражений. Урок-сказка
Упрощение выражений. Урок-сказка Математика 2 класс Название компонентов и результата действия деления
Математика 2 класс Название компонентов и результата действия деления Итерактивная мозаика
Итерактивная мозаика Решение задач на применение первого признака равенства треугольников
Решение задач на применение первого признака равенства треугольников Теория вероятностей. Основные законы распределения случайных величин
Теория вероятностей. Основные законы распределения случайных величин Умножение дроби на натуральное число
Умножение дроби на натуральное число Презентация на тему Четные и нечетные функции
Презентация на тему Четные и нечетные функции Признаки равенства треугольников. Задачи
Признаки равенства треугольников. Задачи Натуральные числа. Подготовка к контрольной работе
Натуральные числа. Подготовка к контрольной работе Логика высказываний. Таблицы истинности
Логика высказываний. Таблицы истинности Ломаная линия
Ломаная линия Математика
Математика Дисперсионный анализ
Дисперсионный анализ Углы. Измерение углов
Углы. Измерение углов Арифметическая и геометрическая прогрессии. Урок обобщения и систематизации знаний
Арифметическая и геометрическая прогрессии. Урок обобщения и систематизации знаний Решение задач по теме "Окружность"
Решение задач по теме "Окружность" Развитие математики в России
Развитие математики в России