Содержание
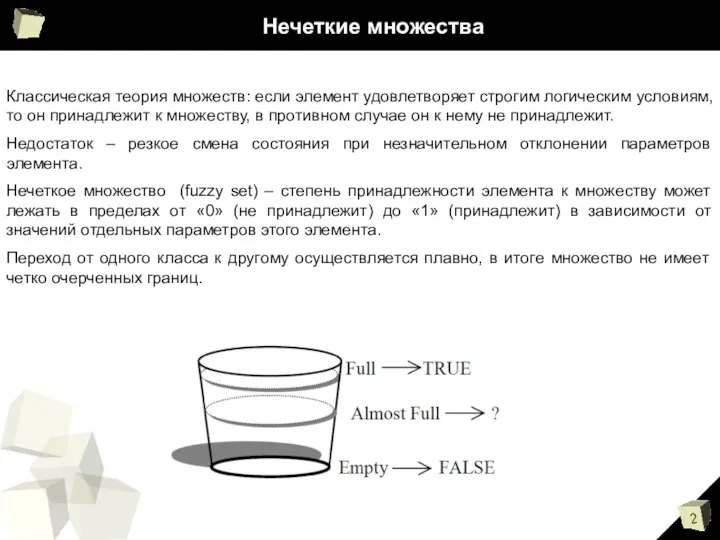
- 2. Нечеткие множества Классическая теория множеств: если элемент удовлетворяет строгим логическим условиям, то он принадлежит к множеству,
- 3. История возникновения Увеличение сложности рассматриваемых систем неизбежно приводит к усложнению способов их описания и управления. При
- 4. Лингвистические переменные Классическая логика оперирует строгими соотношениями, например, Т Таким образом, даже незначительное изменение этой величины
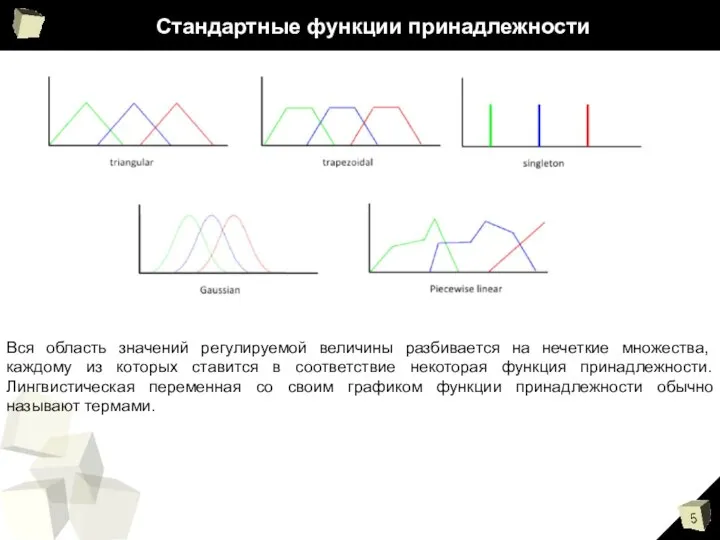
- 5. Стандартные функции принадлежности Вся область значений регулируемой величины разбивается на нечеткие множества, каждому из которых ставится
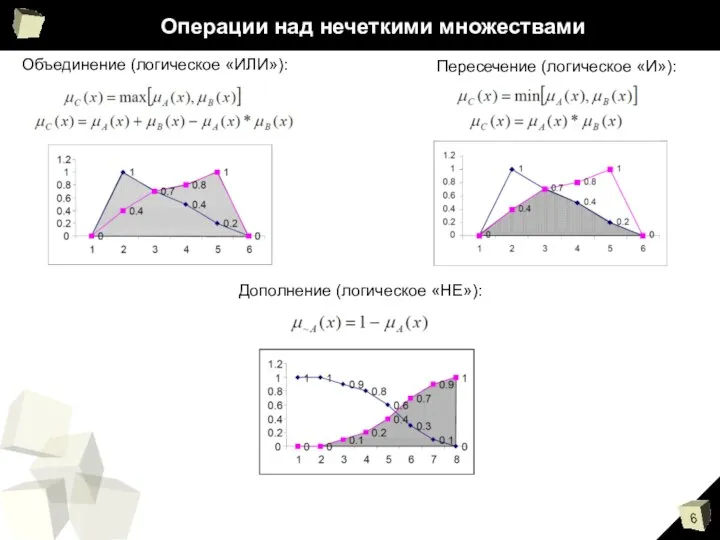
- 6. Операции над нечеткими множествами Объединение (логическое «ИЛИ»): Пересечение (логическое «И»): Дополнение (логическое «НЕ»):
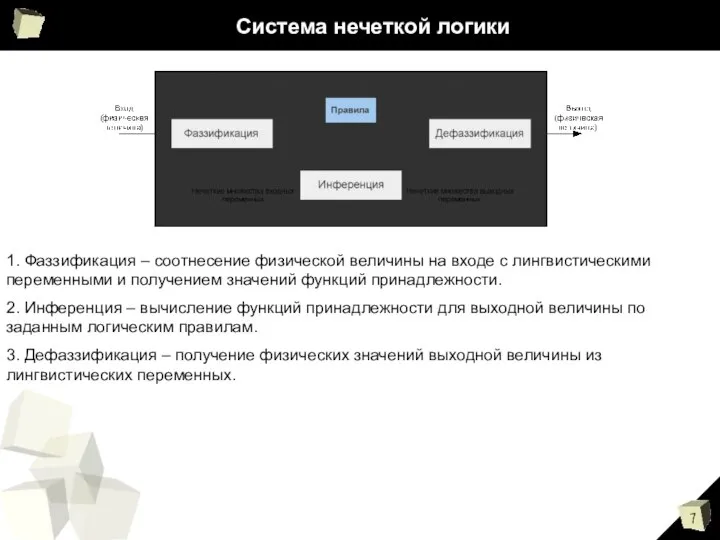
- 7. Система нечеткой логики 1. Фаззификация – соотнесение физической величины на входе с лингвистическими переменными и получением
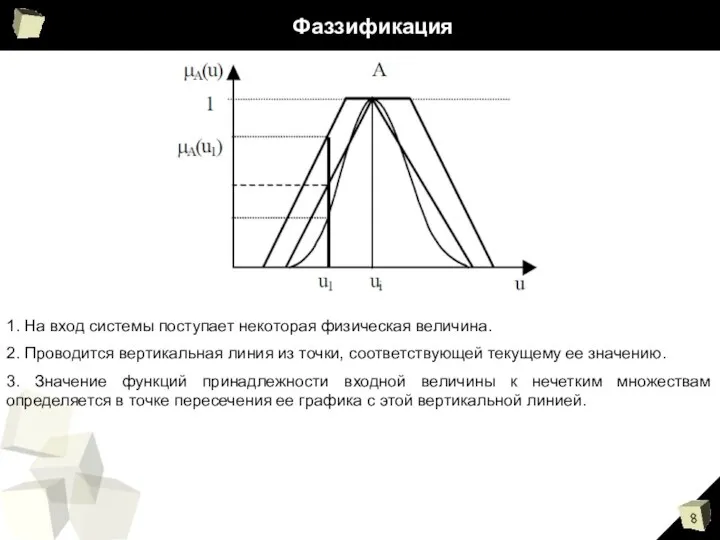
- 8. Фаззификация 1. На вход системы поступает некоторая физическая величина. 2. Проводится вертикальная линия из точки, соответствующей
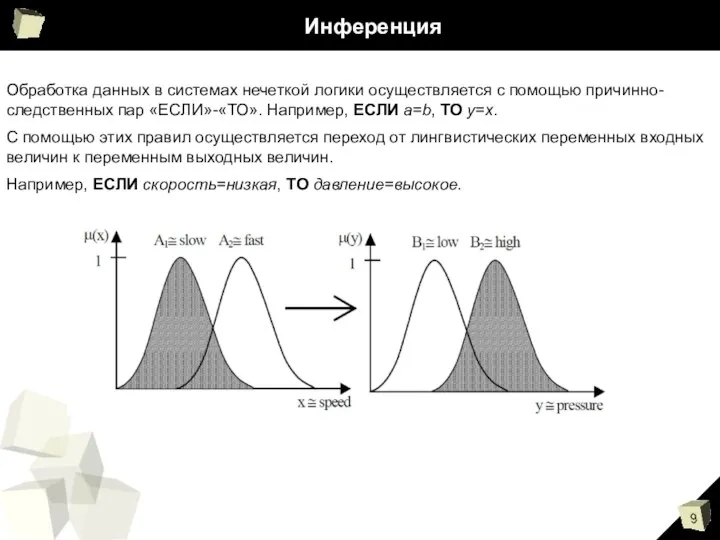
- 9. Инференция Обработка данных в системах нечеткой логики осуществляется с помощью причинно-следственных пар «ЕСЛИ»-«ТО». Например, ЕСЛИ a=b,
- 10. Инференция Обычно правила в системах нечеткой логики состоят из многих компонентов, которые можно классифицировать по следующим
- 11. Инференция Процесс инференции можно разделить на три этапа: 1) Агрегация – объединение с помощью логических операций
- 12. Объединение правил (аккумуляция) В большинстве случаев термы лингвистических переменных выбирают так, чтобы они накладывались друг на
- 13. Дефаззификация Последним этапом работы системы с нечеткой логикой является дефаззификация, в ходе которой вычисляется численное значение
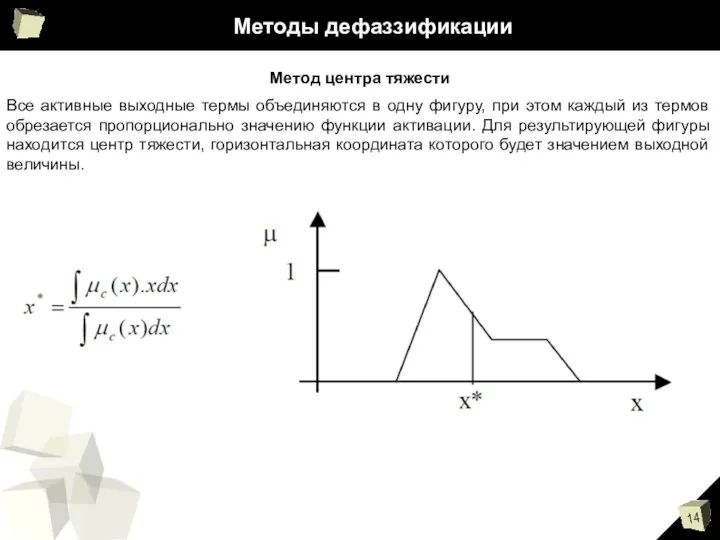
- 14. Методы дефаззификации Метод центра тяжести Все активные выходные термы объединяются в одну фигуру, при этом каждый
- 15. Методы дефаззификации Метод средневзвешенного значения Применим только для симметричных функций принадлежности. Значение выходной величины вычисляется как
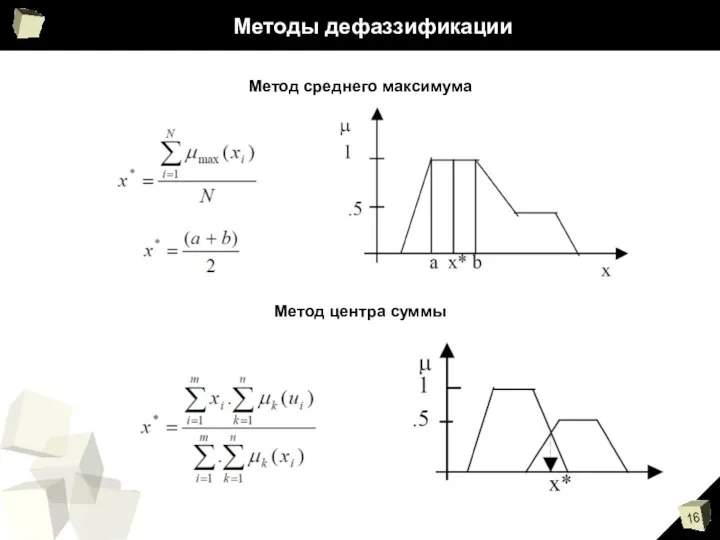
- 16. Методы дефаззификации Метод среднего максимума Метод центра суммы
- 18. Скачать презентацию







 Статистические таблицы
Статистические таблицы Для каждого графика укажите соответствующую формулу
Для каждого графика укажите соответствующую формулу «Проценты» 5 класс Учитель математики МБОУ СОШ № 11, г. Кропоткин Бутенко Елена Константиновна
«Проценты» 5 класс Учитель математики МБОУ СОШ № 11, г. Кропоткин Бутенко Елена Константиновна Математический турнир
Математический турнир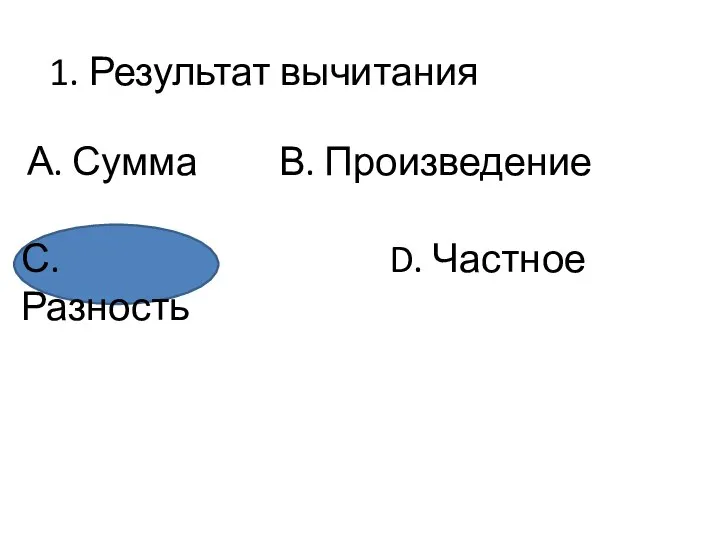 Игра
Игра Арифметическая прогрессия
Арифметическая прогрессия Число и цифра 4
Число и цифра 4 Решение логарифмических уравнений и неравенств. Урок-соревнование по математике в 11 классе
Решение логарифмических уравнений и неравенств. Урок-соревнование по математике в 11 классе Закон звезды, или геометрические построения в орнаменте. Деление окружности
Закон звезды, или геометрические построения в орнаменте. Деление окружности Сложение и вычитание векторов
Сложение и вычитание векторов Перестановки, размещения, cочетания, вероятность
Перестановки, размещения, cочетания, вероятность Проверка умножения (3 класс)
Проверка умножения (3 класс) Поняття та призначення функцій
Поняття та призначення функцій Рефлексия. Графический диктант
Рефлексия. Графический диктант Сложение и вычитание в пределах 10
Сложение и вычитание в пределах 10 Готовимся к ГИА, 9 класс. Тест 4, часть 2
Готовимся к ГИА, 9 класс. Тест 4, часть 2 Функции и их свойства. (9 класс)
Функции и их свойства. (9 класс) Прямая и обратная пропорциональные зависимости
Прямая и обратная пропорциональные зависимости Определители второго и третьего порядка
Определители второго и третьего порядка Отношения. Решение задач
Отношения. Решение задач Теорема Виета. Устная работа. Проверка выполнения домашней работы
Теорема Виета. Устная работа. Проверка выполнения домашней работы Готовимся к ЕГЭ. Задания В 8 и В 14
Готовимся к ЕГЭ. Задания В 8 и В 14 Сложение и вычитание смешанных чисел. 5 класс
Сложение и вычитание смешанных чисел. 5 класс Презентация по теме: «Числа с собственными именами».
Презентация по теме: «Числа с собственными именами». Умножение смешанных чисел
Умножение смешанных чисел Однородная система линейных алгебраических уравнений. Фундаментальная система решений
Однородная система линейных алгебраических уравнений. Фундаментальная система решений Сумма углов треугольника. Внешний угол треугольника. Математический диктант
Сумма углов треугольника. Внешний угол треугольника. Математический диктант Модуль числа
Модуль числа